【DFT+k·p模型】三阶拓扑绝缘体：墙纸费米子

转载自公众平台：npj计算材料学

本文以传播知识为目的，如有侵权请后台联系我们，我们将在第一时间删除。

近年来，受对称保护的拓扑量子态引起了人们的广泛兴趣，特别是当包含晶体对称性时，拓扑电子态的分类非常丰富。一个著名的例子是由对称镜像或旋转对称保护的拓扑晶体绝缘体，其双简并表面费米子出现在特定表面上，保持相应的点式对称。直到最近，这种拓扑分类才开始延伸到非点式对称：点群操作和分数平移的组合。物理上，表面态的简并和相容关系可以约束为17个二维墙纸群的不可约共表示，沙漏费米子、Möbius绝缘体和四重简并狄拉克费米子在四种非点式墙纸群（pg、pmg、pgg、p4g）中都得到了很好的研究。

 

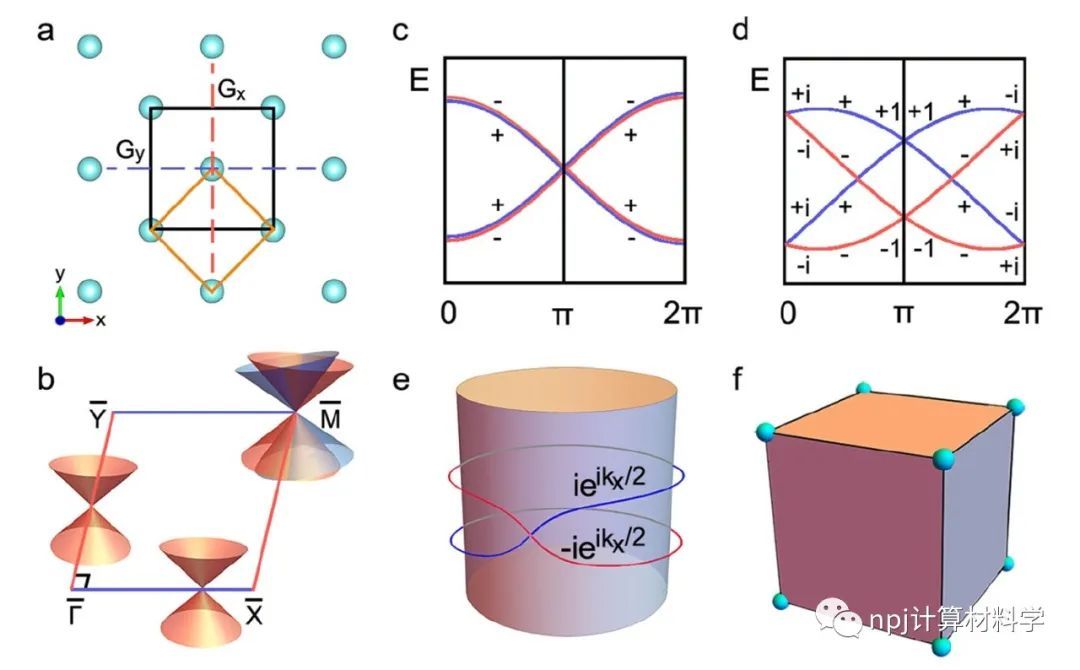Fig. 1 Schematic demonstration for the wallpaper fermions and third-order topology.

另一方面，晶体对称性打开了拓扑体边对应的视界，扩展了量子化的四极矩或八极矩，揭示了高阶拓扑绝缘体的存在。高阶拓扑绝缘体的拓扑结构定位于具有手性或螺旋模态的铰链和/或角上，这可由嵌套的Wilson环区分。尽管人们正在积极探索高阶拓扑绝缘体，但大量工作主要集中在二阶拓扑绝缘体上，且其已经在一些超材料（如微波、电路、声学）和电子材料（如Bi和Bi4Br4）中通过实验观察到。而三阶拓扑绝缘体只局限于超材料，且能够包括分数角电荷、填充异常等奇异量子现象的电子材料迄今为止还没有。

Fig. 2 Material candidates of wallpaper fermion and third-order topological insulators.

来自山东大学物理学院晶体材料国家重点实验室的戴瑛、牛成旺教授课题组（去年7月），利用k.p模型和第一性计算提出了Tl4XTe3（X = Pb/Te）是实现墙纸费米子和三阶拓扑绝缘体很有前途的候选材料。由于非点式墙纸群中的两个垂直滑移面，墙纸费米子包括沙漏费米子、四重简并狄拉克费米子和Möbius费米子出现在表面光谱中。与之前报告中的非平庸墙纸费米子不同，广义的Z4不变量在这里是平庸的，它显著地呈现了间隙Wilson环，并允许实现三阶拓扑绝缘体性质的嵌套Wilson环。特别地，其将三阶拓扑推广到非点式对称性，实现了Tl4XTe3系统中的三阶拓扑相。

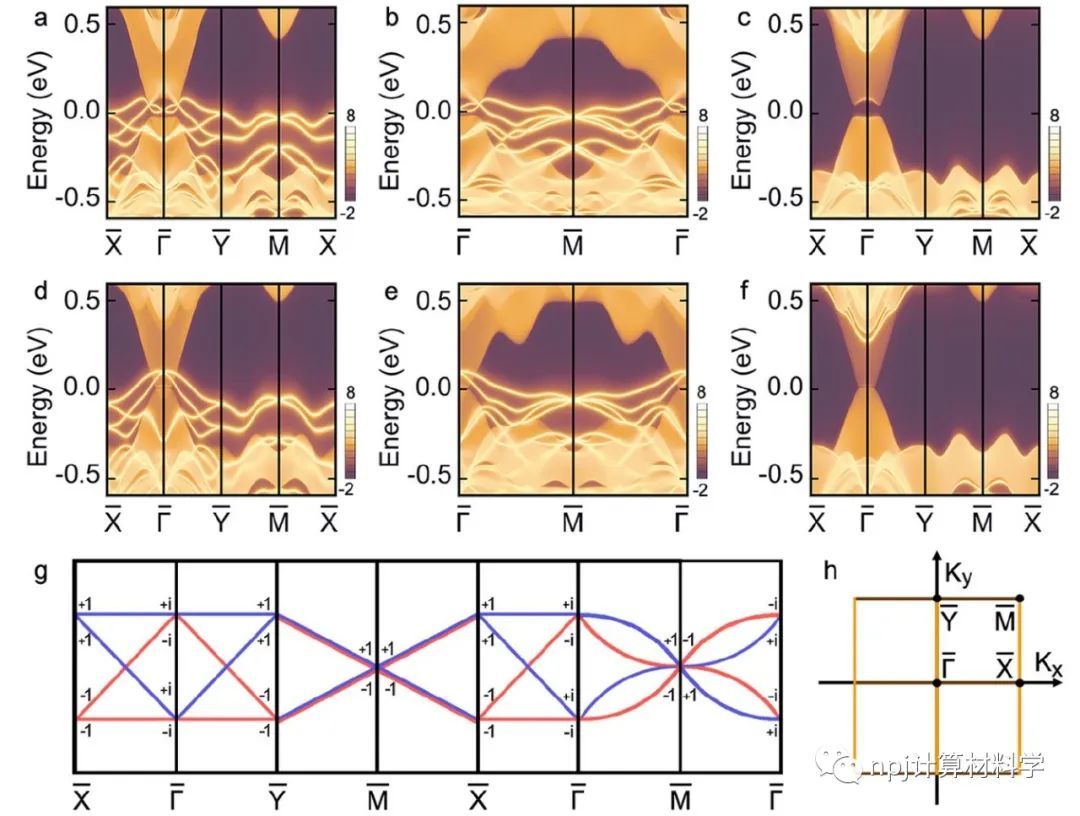Fig. 3 Surface spectrum for wallpaper fermion.

由于时间反演对称，角态以Kramers对的形式出现，且八极极化为零，这与超材料中实现的量子化八极拓扑绝缘体不同。每一个Kramers对都有一个非平凡的八极极化，导致一个非平凡的时间反转极化八极极化。这些发现可能会激发拓扑现象和奇异拓扑态在自旋电子学中的应用。该文近期发布于npj Computational Materials 8: 154 (2022).

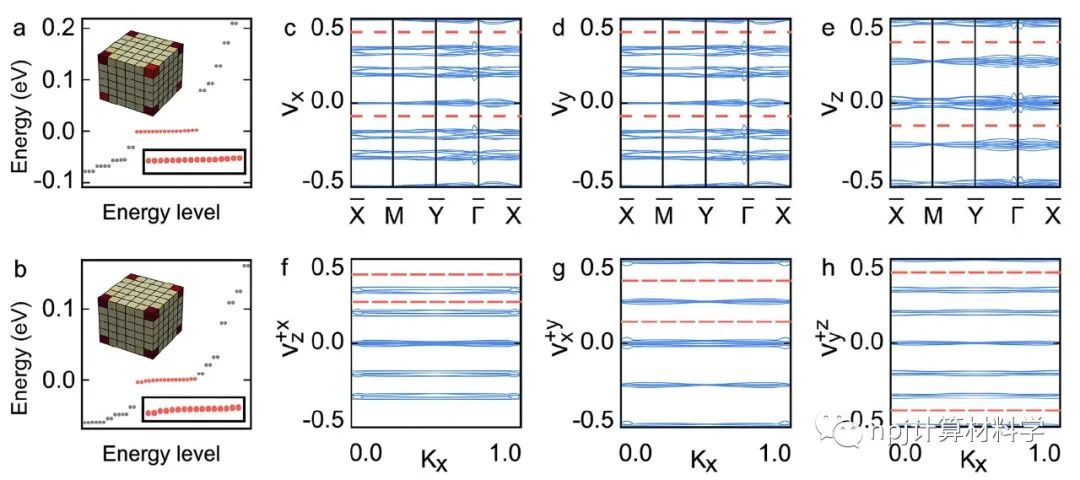
Fig. 4 Nontrivial helical corner states.

Editorial Summary

Third-order topological insulators: Wallpaper fermionsin 

Much of the recent interest has been prompted by the symmetry-protected topological quantum states, and in particular, the classification of topological electronic states is greatly enriched while including the crystalline symmetries. A notable example is the topological crystalline insulator (TCI) protected by the symmorphic mirror or rotation symmetry, where twofold degenerate surface fermions appear on particular surfaces preserving the corresponding symmorphic symmetry. Only recently, this topological classification has started to reach out to the nonsymmorphic symmetries, combinations of point group operations and fractional translations. Physically, the degeneracy and compatibility relation of surface states can be constrained to the irreducible co-representation of 17 two-dimensional (2D) wallpaper groups, and the hourglass fermion, Möbius insulators, and fourfold-degenerate Dirac fermion have been well studied in the all four nonsymmorphic wallpaper groups, pg, pmg, pgg and p4g. On the other hand, the crystalline symmetries open up a horizon of topological bulk–boundary correspondence, extended with quantized quadrupole or octupole moments, revealing the presence of higher-order topological insulators (HOTIs). The topology of HOTIs is localized at hinges and/or corners with chiral or helical modes, which is distinguished by the nested Wilson loop. Despite being actively explored, efforts have mainly focused on the second-order topological insulators (SOTIs), which have been observed experimentally in both the metamaterials such as microwave, electrical circuit, and acoustics, and the electronic materials such as Bi and Bi4Br4. The three-order topological insulators (TOTIs) have only been limited to metamaterials, explicit electronic materials that enable the exploration of exotic quantum phenomena, including fractional corner charges and filling anomaly, have so far been missing. 

A group led by Prof. Ying Dai and Pro.f Chengwang Niu from the State Key Laboratory of Crystal Materials, Shandong University, proposed Tl4XTe3 (X = Pb/Te) as promising material candidates for both wallpaper fermions and TOTIs by using k·p models and ab-initio calculations. Due to the existence of two perpendicular glide planes, wallpaper fermions including hourglass fermion, fourfold degenerate Dirac fermion, and Möbius fermion emerge in the surface spectrum. However, unlike nontrivial wallpaper fermions in the previous reports, the generalized Z4invariant is trivial in these materials, which remarkably renders a gapped Wilson loop and allows us to implement the nested Wilson loop for the TOTIs nature. Especially, the authors generalized the third-order topology to nonsymmorphic symmetries, realizing the TOTI phase in the Tl4XTe3system. Due to the existence of time-reversal symmetry, corner states come in Kramers pair and have a zero octupole polarization, which is different from the quantized octupole TIs achieved in metamaterials. Each one of the Kramers pair has a nontrivial octupole polarization, leading to a nontrivial time-reversal polarized octupole polarization. These findings may motivate the formulation of strategies for finding topological phenomena and exotic topological states for spintronics applications. This article was recently published in npj Computational Materials 8: 154 (2022).

原文Abstract及其翻译

Third-order topological insulators with wallpaper fermions in Tl4PbTe3 and Tl4SnTe3 (Tl4PbTe3和Tl4SnTe3中实现墙纸费米子的三阶拓扑绝缘体)

Ning Mao, Hao Wang, Ying Dai, Baibiao Huang & Chengwang Niu

Abstract Nonsymmorphic symmetries open up horizons of exotic topological boundary states and even generalize the bulk–boundary correspondence, which, however, the third-order topological insulator in electronic materials are still unknown. Here, by means of the symmetry analysis and k · p models, we uncover the emergence of long-awaited third-order topological insulators and the wallpaper fermions in space group I4/mcm (No.140). Based on this, we present the hourglass fermion, fourfold-degenerate Dirac fermion, and Möbius fermion in the (001) surface of Tl4XTe3(X = Pb/Sn) with a nonsymmorphic wallpaper group p4g. Remarkably, 16 helical corner states reside on eight corners in Kramers pair, rendering the real electronic material of third-order topological insulators. More importantly, a time-reversal polarized octupole polarization is defined to uncover the nontrivial third-order topology, as is implemented by the 2nd and 3rd order Wilson loop calculations. Our results could considerably broaden the range of wallpaper fermions and lay the foundation for future experimental investigations of third-order topological insulators.

摘要非点式对称打开了奇异拓扑边界态的视野，甚至推广了体边对应关系，而电子材料中的三阶拓扑绝缘体仍然是未知的。在这里，我们通过对称性分析和k.p模型，在空间群I4/mcm（No.140）中发现了期待已久的三阶拓扑绝缘体和Wallpaper费米子。在此基础上，我们提出了在具有非点式墙纸群p4g的Tl4XTe3（X = Pb/Sn）（001）表面的沙漏费米子、四重简并Dirac费米子和Mobius费米子。值得注意的是，在Kramers对的8个角上存在16个螺旋角态，呈现出真正的三阶拓扑绝缘体电子材料。更重要的是，我们定义了一个时间反转极化八极极化来揭示非平凡的三阶拓扑，这是通过计算二阶和三阶Wilson环实现的。我们的研究结果可以大大拓宽墙纸费米子的研究范围，并为今后三阶拓扑绝缘体的实验研究奠定基础。