【数据关联（3）】​5月9日数据匹配图论、匈牙利、KM算法,多目标跟踪

修订 ：多目标跟踪，即MOT（Multi-Object Tracking），也就是在一段视频中同时跟踪多个目标20200521

英文注解

无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）

背景知识

• 图论（来源于《数据结构》）

1.1基本概念：

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

图论是一种表示 “多对多” 的关系

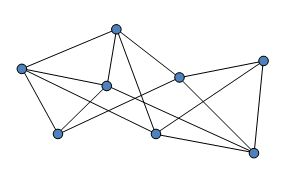
图论是一种表示 “多对多” 的关系

图是由顶点和边组成的：(可以无边，但至少包含一个顶点)

• 一组顶点：通常用 V(vertex) 表示顶点集合
• 一组边：通常用 E(edge) 表示边的集合

图可以分为有向图和无向图，在图中：

• (v, w) 表示无向边，即 v 和 w 是互通的
• <v, w> 表示有向边，该边始于 v，终于 w

图可以分为有权图和无权图：

• 有权图：每条边具有一定的权重(weight)，通常是一个数字
• 无权图：每条边均没有权重，也可以理解为权为 1

图又可以分为连通图和非连通图：

• 连通图：所有的点都有路径相连
• 非连通图：存在某两个点没有路径相连

图中的顶点有度的概念：

• 度(Degree)：所有与它连接点的个数之和
• 入度(Indegree)：存在于有向图中，所有接入该点的边数之和
• 出度(Outdegree)：存在于有向图中，所有接出该点的边数之和

1.2 图的表示：

图在程序中的表示一般有两种方式：

1.2.1邻接矩阵：

在 n 个顶点的图需要有一个 n × n 大小的矩阵
在一个无权图中，矩阵坐标中每个位置值为 1 代表两个点是相连的，0 表示两点是不相连的
在一个有权图中，矩阵坐标中每个位置值代表该两点之间的权重，0 表示该两点不相连
在无向图中，邻接矩阵关于对角线相等

1.2.2 邻接链表：

对于每个点，存储着一个链表，用来指向所有与该点直接相连的点
对于有权图来说，链表中元素值对应着权重

例如在

无向无权图中：

在无向有权图中：

可以看出在无向图中，邻接矩阵关于对角线对称，而邻接链表总有两条对称的边

而在有向无权图中：

邻接矩阵和链表对比：
邻接矩阵由于没有相连的边也占有空间，因此存在浪费空间的问题，而邻接链表则比较合理地利用空间
邻接链表比较耗时，牺牲很大的时间来查找，因此比较耗时，而邻接矩阵法相比邻接链表法来说，时间复杂度低。

1.3 图的遍历：

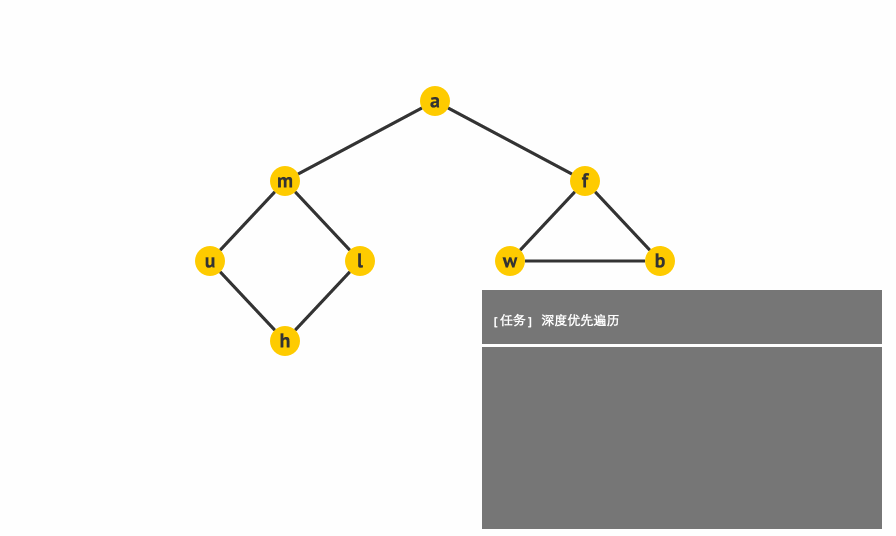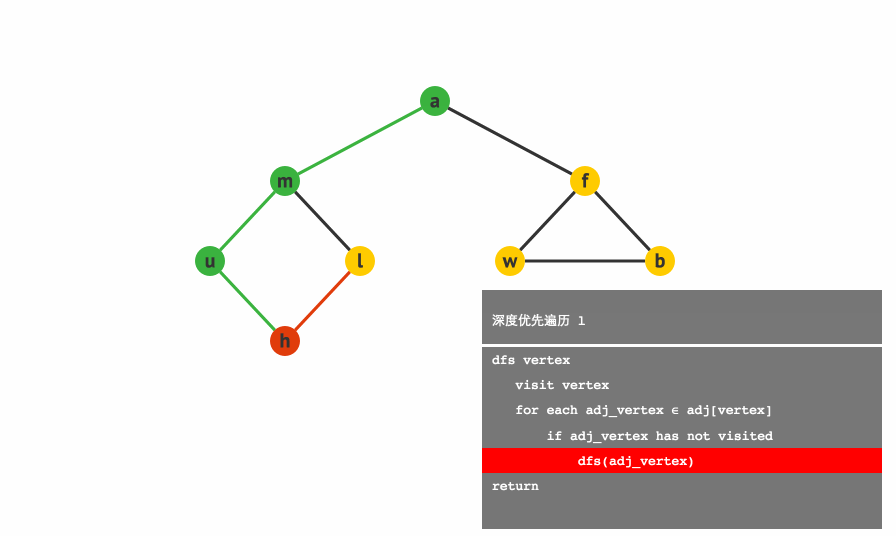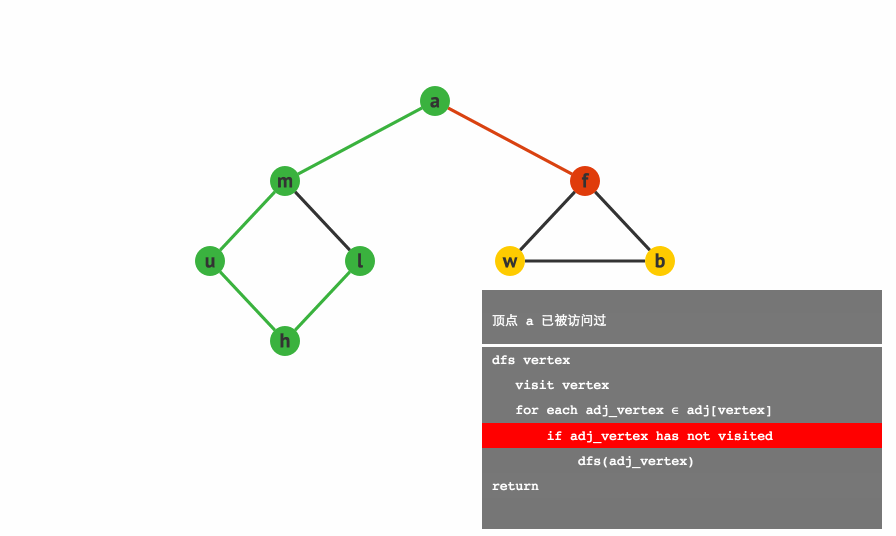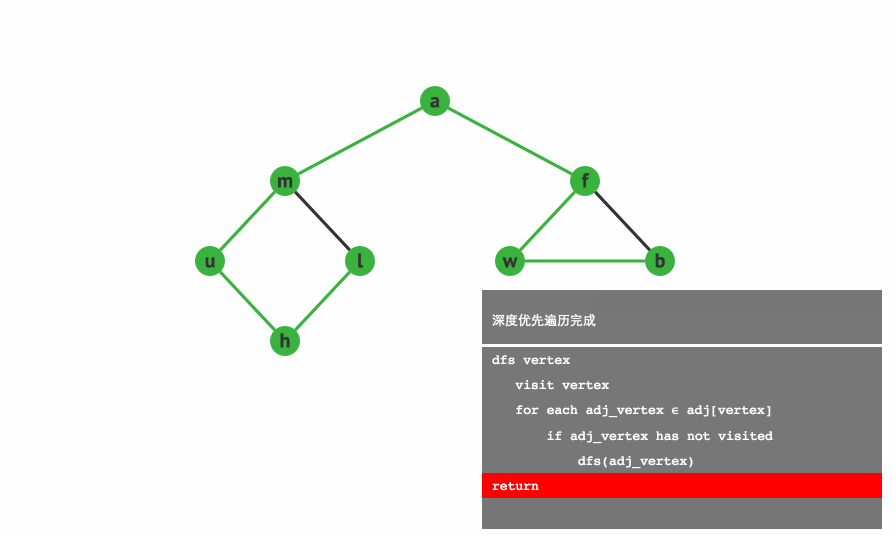
1.3.1 深度优先遍历：(Depth First Search, DFS)

基本思路：深度优先遍历图的方法是，从图中某顶点 v 出发

1：访问顶点 v
2：从 v 的未被访问的邻接点中选取一个顶点 w，从 w 出发进行深度优先遍历
3：重复上述两步，直至图中所有和v有路径相通的顶点都被访问到

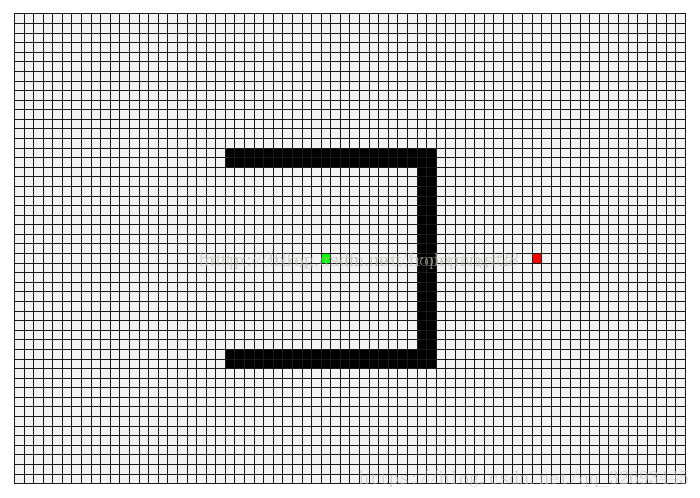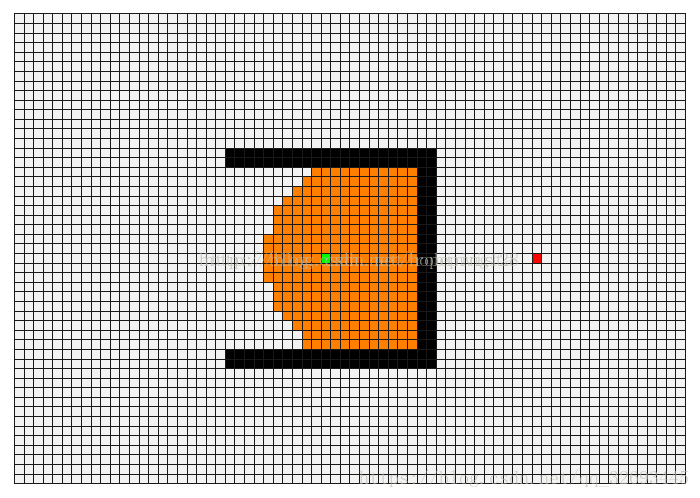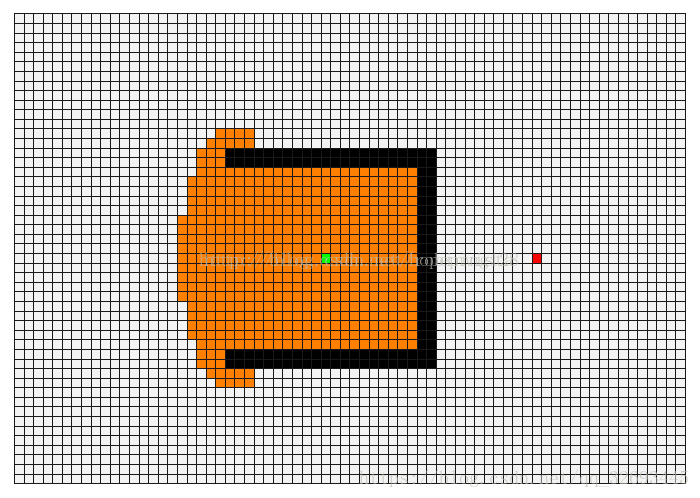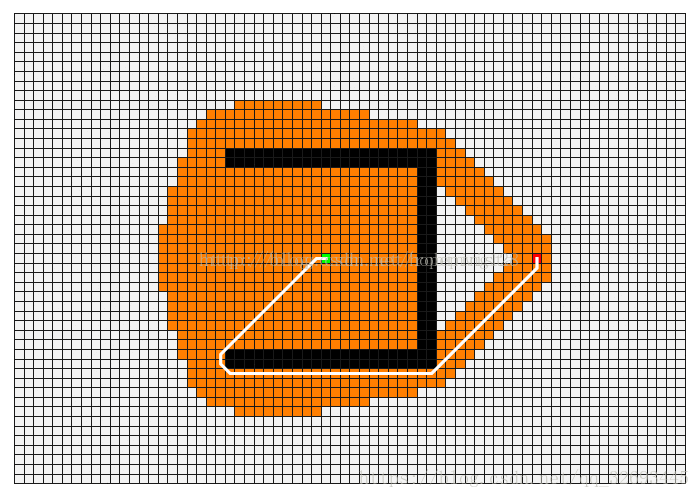
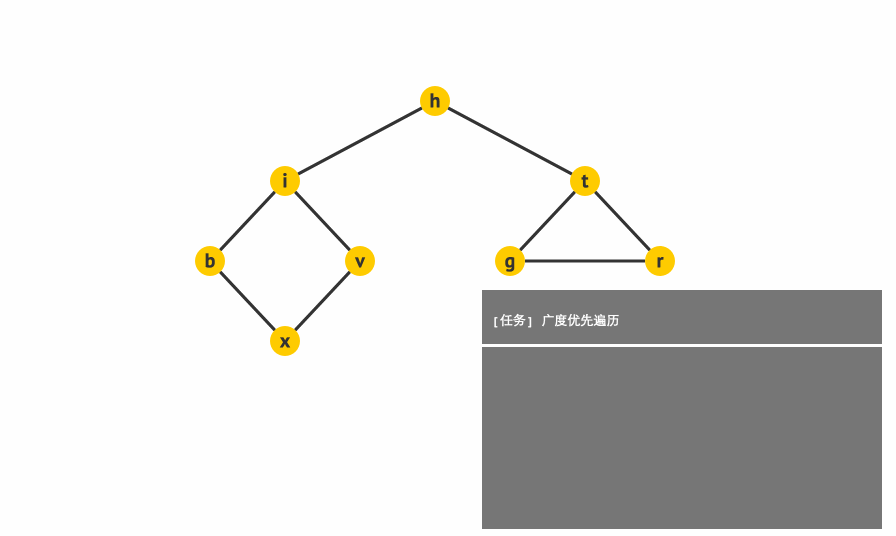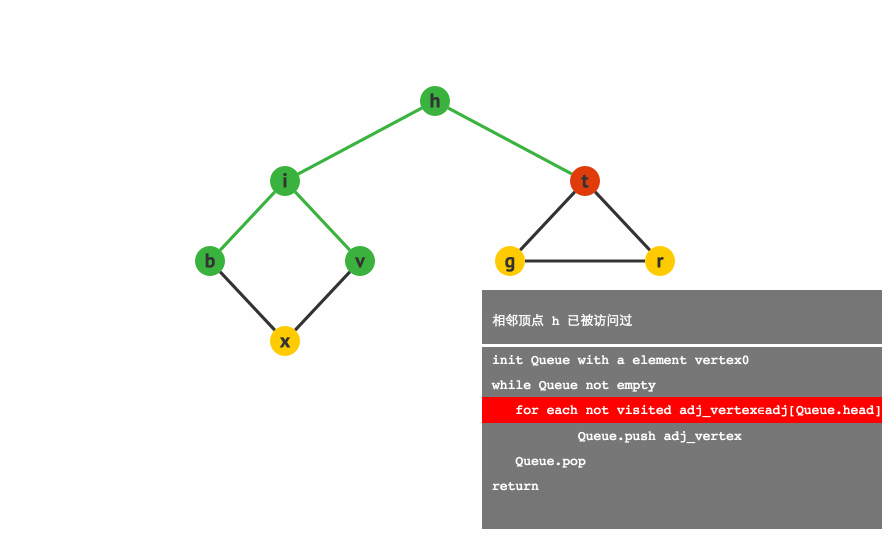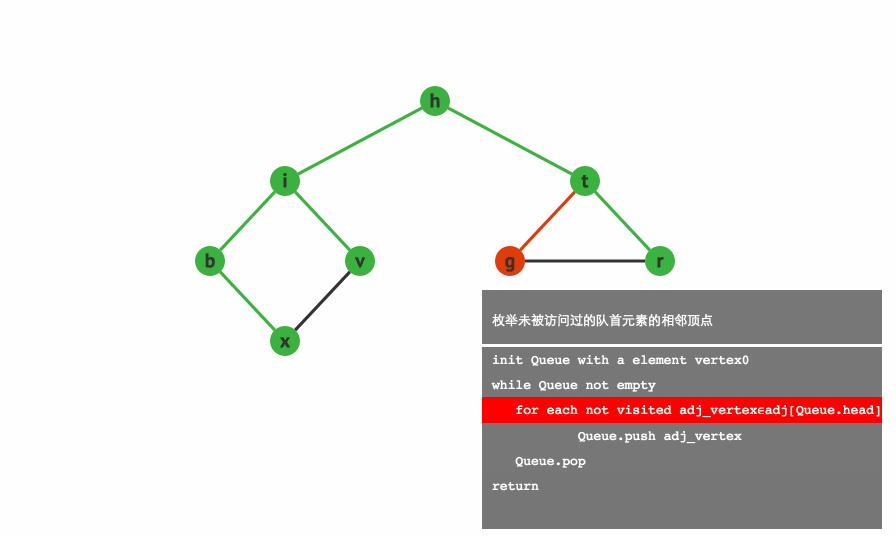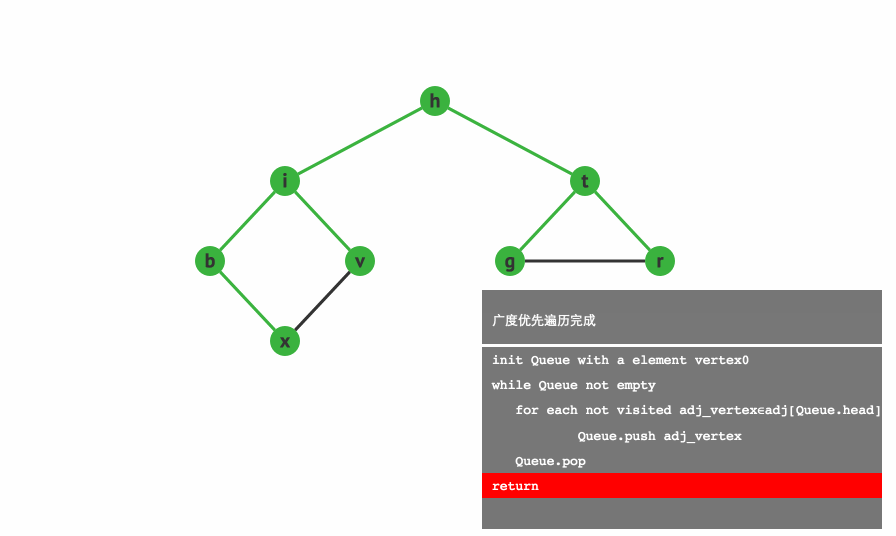
1.3.2 广度优先搜索：(Breadth First Search, BFS)

广度优先搜索，可以被形象地描述为 “浅尝辄止”，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。

实现思路：

1、顶点 v 入队列
2、当队列非空时则继续执行，否则算法结束
3、出队列取得队头顶点 v；访问顶点 v 并标记顶点 v 已被访问
4、查找顶点 v 的第一个邻接顶点 col
5、若 v 的邻接顶点 col 未被访问过的，则 col 继续
6、查找顶点 v 的另一个新的邻接顶点 col，转到步骤 5 入队列，直到顶点 v 的所有未被访问过的邻接点处理完。转到步骤 2

1.3.3 辩证理解

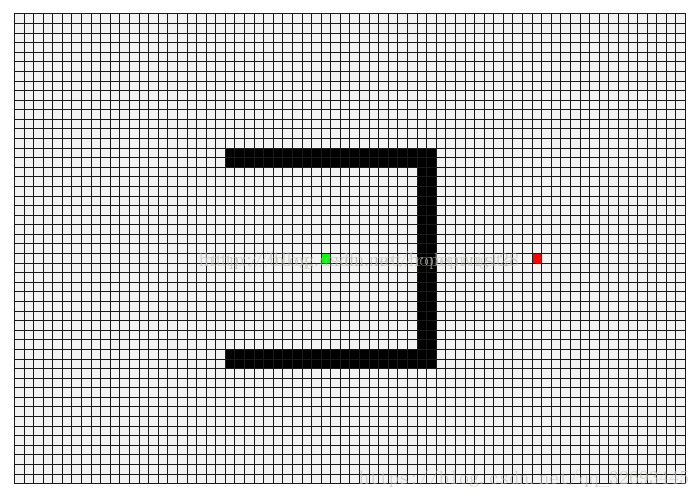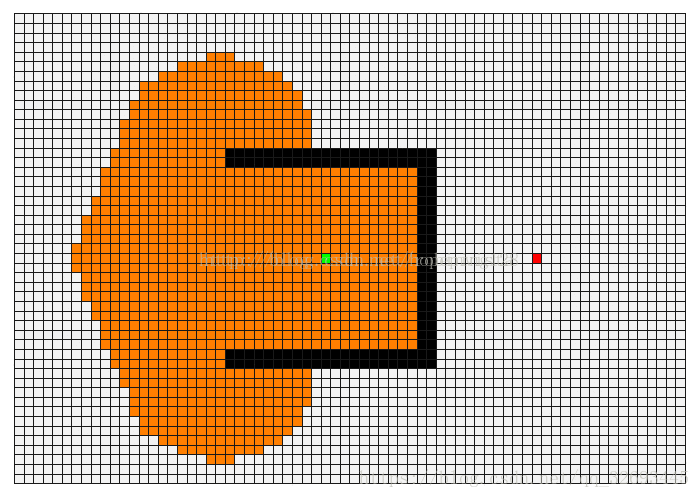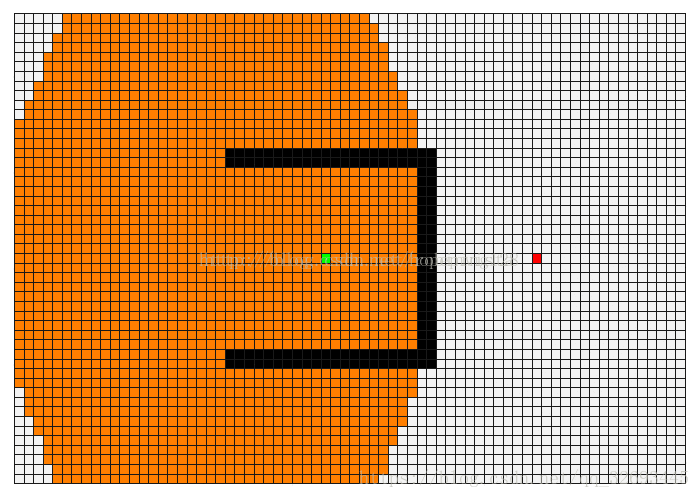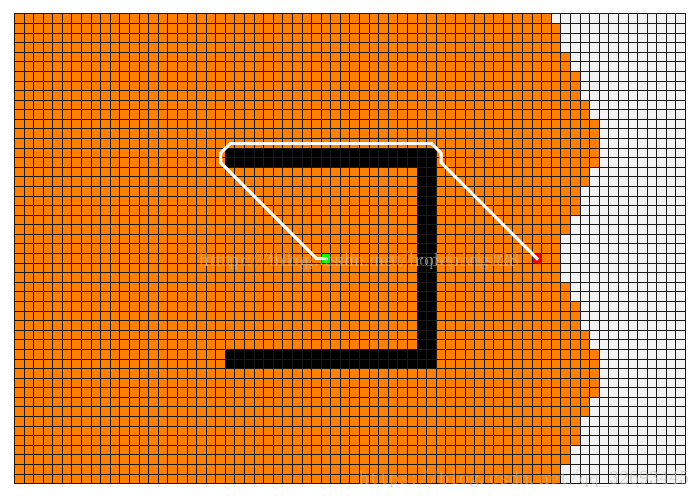
要理解深度优先和广度优先搜索，首先要理解搜索步，一个完整的搜索步包括两个处理

1、获得当前位置上，有几条路可供选择
2、根据选择策略，选择其中一条路，并走到下个位置

相当于在漆黑的夜里，你只能看清你站的位置和你前面的路，但你不知道每条路能够通向哪里。搜索的任务就是，给出初始位置和目标位置，要求找到一条到达目标的路径。

深度优先就是，从初始点出发，不断向前走，如果碰到死路了，就往回走一步，尝试另一条路，直到发现了目标位置。这种不撞南墙不回头的方法，即使成功也不一定找到一条好路，但好处是需要记住的位置比较少。
广度优先就是，从初始点出发，把所有可能的路径都走一遍，如果里面没有目标位置，则尝试把所有两步能够到的位置都走一遍，看有没有目标位置；如果还不行，则尝试所有三步可以到的位置。这种方法，一定可以找到一条最短路径，但需要记忆的内容实在很多，要量力而行。

1.4 最短路径算法 (Shortest Path Algorithm)

1. 无权图：

2. 有权图：
   在有权图中，常见的最短路径算法有 Dijkstra 算法 Floyd 算法

• 迪杰斯特拉 Dijkstra 算法：Dijkstra 算法适用于权值为正的的图
• 佛洛伊德 Floyd 算法：可以求出任意两点的最短距离

1.5 最小生成树 (Minimum Spanning Trees MST)

例如：要在 n 个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树

• 1. 普里姆算法 (Prim 算法):
• 2. Kruskal 算法：需要一个集合用来升序存储所有边

参考：
https://www.cnblogs.com/skywang12345/p/3603935.html
https://zhuanlan.zhihu.com/p/25498681

国家分配好朋友

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。

• 是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。
• 如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

二分图匹配

二分图又称作二部图，是图论中的一种特殊模型。

设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。
可以得到线上的driver与order之间的匹配关系既是一个二分图。

简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。
准确地说：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。

二分图的一个等价定义是：不含有「含奇数条边的环」的图。

图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

https://www.cnblogs.com/shenben/p/5573788.html
最小点覆盖：假如选了一个点就相当于覆盖了以它为端点的所有边，你需要选择最少的点来覆盖所有的边

最小割定理：是一个二分图中很重要的定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

最小点集覆盖==最大匹配。在这里解释一下原因，首先，最小点集覆盖一定>=最大匹配，因为假设最大匹配为n，那么我们就得到了n条互不相邻的边，光覆盖这些边就要用到n个点。现在我们来思考为什么最小点击覆盖一定<=最大匹配。任何一种n个点的最小点击覆盖，一定可以转化成一个n的最大匹配。因为最小点集覆盖中的每个点都能找到至少一条只有一个端点在点集中的边（如果找不到则说明该点所有的边的另外一个端点都被覆盖，所以该点则没必要被覆盖，和它在最小点集覆盖中相矛盾），只要每个端点都选择一个这样的边，就必然能转化为一个匹配数与点集覆盖的点数相等的匹配方案。所以最大匹配至少为最小点集覆盖数，即最小点击覆盖一定<=最大匹配。综上，二者相等。

3. KM算法初步

KM算法全称是Kuhn-Munkras，是这两个人在1957年提出的，

3.1 交替路：

从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

3.2 增广路径作用与定义

作用：
增广路主要应用于匈牙利算法中，用于求二分图最大匹配。

定义：
若P是图G中一条连通两个未匹配顶点的路径，并且属于Matching（简写M）的边和不属于Matching（简写M）的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径【百度百科】

具体的：
从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。

其他性质：【百度百科】
由增广路的定义可以推出下述五个结论：
1－P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
2－不断寻找增广路可以得到一个更大的匹配M’，直到找不到更多的增广路。
3－M为G的最大匹配当且仅当不存在M的增广路径。
4－最大匹配数M+最大独立数N=总的结点数
5 – 二分图的最小路径覆盖数 = 原图点数 - 最大匹配数

增广路径有如下特性：

1. 有奇数条边
2. 起点在二分图的X边，终点在二分图的Y边
3. 路径上的点一定是一个在X边，一个在Y边，交错出现。
4. 整条路径上没有重复的点
5. 起点和终点都是目前还没有配对的点，其他的点都已经出现在匹配子图中
6. 路径上的所有第奇数条边都是目前还没有进入目前的匹配子图的边，而所有第偶数条边都已经进入目前的匹配子图。奇数边比偶数边多一条边
7. 于是当我们把所有第奇数条边都加到匹配子图并把条偶数条边都删除，匹配数增加了1.

例如下图，淡蓝色路径x0y0的是当前的匹配子图，通过x1找到了增广路径粉红色路径：x1y0->y0x0->x0y2

增广路径有两种寻径方法，一个是深搜，一个是宽搜。

例如从x2出发寻找增广路径

• 如果是深搜，x2找到y0匹配，但发现y0已经被x1匹配了，于是就深入到x1，去为x1找新的匹配节点，结果发现x1没有其他的匹配节点，于是匹配失败，x2接着找y1，发现y1可以匹配，于是就找到了新的增广路径。
• 如果是宽搜，x2找到y0节点的时候，由于不能马上得到一个合法的匹配，于是将它做为候选项放入队列中，并接着找y1，由于y1已经匹配，于是匹配成功返回了。
  相对来说，深搜要容易理解些，其栈可以由递归过程来维护，而宽搜则需要自己维护一个队列，并对一路过来的路线自己做标记，实现起来比较麻烦。

4.0 匈牙利树

是在1965年提出的。
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。

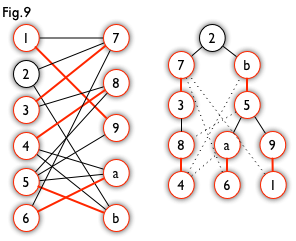
匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树

这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。

如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示

• （顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

5.0 匈牙利算法——最大匹配

用于求二分图的最大匹配。何为最大匹配？假设每条边有权值，那么一定会存在一个最大权值的匹配情况。

5.1 匈牙利算法步骤

算法根据一定的规则选择二分图的边加入匹配子图中，其基本模式为：
1.初始化匹配子图为空
2.While 找得到增广路径
3.Do 把增广路径添加到匹配子图中

5.2 最大匹配的讲解 ：匈牙利算法（二分图）

由增广路的性质，增广路中的匹配边总是比未匹配边多一条，所以如果我们放弃一条增广路中的匹配边，选取未匹配边作为匹配边，则匹配的数量就会增加。匈牙利算法就是在不断寻找增广路，如果找不到增广路，就说明达到了最大匹配。

先给一个例子
1、起始没有匹配

2、选中第一个x点找第一跟连线

3、选中第二个点找第二跟连线

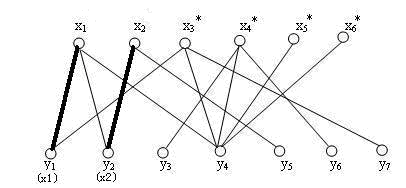
4、发现x3的第一条边x3y1已经被人占了，找出x3出发的的交错路径x3-y1-x1-y4，把交错路中已在匹配上的边x1y1从匹配中去掉，剩余的边x3y1 x1y4加到匹配中去

5、同理加入x4,x5。

匈牙利算法可以深度有限或者广度优先，刚才的示例是深度优先，即x3找y1,y1已经有匹配，则找交错路。若是广度优先，应为：x3找y1,y1有匹配，x3找y2。

5.4 深度优先搜索（又名交叉染色法）实现二分图判定

简要的了解一下图的概念，以及表示、储存的方法。

• 主要就是邻接矩阵和邻接表两种方式
  • 邻接矩阵就不说了比较好实现
  • 邻接表则主要用到不同的容器，比如vector。

使用邻接表的主要思路是对每一个顶点都建立一个vector容器，当它和另一个顶点有边的时候就将该顶点的编号插入vector中，注意无向表还要反过来插入一次

当使用类或者结构体来储存图的顶点和边时就可以添加众多的属性来扩展

接下来就是图的搜索，先以最基本的深度优先搜索为例 其实很简单，就是一个顶点走到头再回来走下一支

现在有一个基本的问题，我们如何判断一个图是否是二分图呢

最简单的思路无非是穷举，对每个顶点我们都可以有两种颜色，采用搜索的思路，如果能走出一条满足任意两个顶点颜色的路径就可以了。

具体的实现方法参考一下书本，大概可以这样想：

• 从一个顶点出发，把所有它相邻的顶点染成另一个颜色。
• 不停的继续这一个过程，一层一层的染色。
• 如果中间不出现矛盾情况（即相邻的顶点同色）就判定为二分图，
• 否则立即返回换一个没有染色的顶点重新尝试（这个的原理需要好好理解）

首先任意取出一个顶点进行染色,和该节点相邻的点有三种情况:
1.如果节点没有染过色，就染上与它相反的颜色，推入队列，
2.如果节点染过色且相反，忽视掉，
3.如果节点染过色且与父节点相同，证明不是二分图，return

6.0 KM算法——最佳匹配

KM算法，用于求二分图匹配的最佳匹配。何为最佳匹配？就是带权二分图的权值最大的完备匹配称为最佳匹配。 那么何为完备匹配？X部中的每一个顶点都与Y部中的一个顶点匹配，或者Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完备匹配。

6.1 KM算法步骤

其算法步骤如下：
1.用邻接矩阵（或其他方法也行啦）来储存图，注意：如果只是想求最大权值匹配而不要求是完全匹配的话，请把各个不相连的边的权值设置为0。
2.运用贪心算法初始化标杆。
3.运用匈牙利算法找到完备匹配。
4.如果找不到，则通过修改标杆，增加一些边。
5.重复3，4的步骤，直到完全匹配时可结束。

6.2 KM算法标杆(又名顶标)的引入

二分图最佳匹配还是二分图匹配，所以跟和匈牙利算法思路差不多。
二分图是特殊的网络流，最佳匹配相当于求最大（小）费用最大流，所以FF算法（全名Ford-Fulkerson算法）也能实现。

• 所以我们可以把这匈牙利算法和FF算法结合起来。这就是KM算法的思路了：尽量找最大的边进行连边，如果不能则换一条较大的。

FF算法里面，我们每次是找最长（短）路进行通流，所以二分图匹配里面我们也按照FF算法找最大边进行连边！
但是遇到某个点被匹配了两次怎么办？那就用匈牙利算法进行更改匹配！

所以，根据KM算法的思路，我们一开始要对边权值最大的进行连线。

那问题就来了，我们如何让计算机知道该点对应的权值最大的边是哪一条？或许我们可以通过某种方式记录边的另一端点，但是呢，后面还要涉及改边，又要记录边权值总和，而这个记录端点方法似乎有点麻烦。

于是KM采用了一种十分巧妙的办法（也是KM算法思想的精髓）：添加标杆(顶标)

6.2.1 添加标杆(顶标)流程：

我们对左边每个点Xi和右边每个点Yi添加标杆Cx和Cy。其中我们要满足Cx+Cy>=w[x][y]（w[x][y]即为点Xi、Yi之间的边权值）
对于一开始的初始化，我们对于每个点分别进行如下操作：Cx=max(w[x][y]); Cy=0;

添加顶标之前的二分图：

添加顶标之后的二分图：

6.4 基本步骤

一般对KM算法的描述，基本上可以概括成以下几个步骤：
（1） 初始化可行标杆
（2） 用匈牙利算法寻找完备匹配
（3） 若未找到完备匹配则修改可行标杆
（4） 重复（2）（3）直到找到相等子图的完备匹配

7.0【KM算法及其具体过程】

（1）可行点标：每个点有一个标号，记lx[i]为X方点i的标号，ly[j]为Y方点j的标号。如果对于图中的任意边(i, j, W)都有lx[i]+ly[j]>=W，则这一组点标是可行的。特别地，对于lx[i]+ly[j]=W的边(i, j, W)，称为可行边；
（2）KM算法的核心思想就是通过修改某些点的标号（但要满足点标始终是可行的），不断增加图中的可行边总数，直到图中存在仅由可行边组成的完全匹配为止，此时这个匹配一定是最佳的（因为由可行点标的的定义，图中的任意一个完全匹配，其边权总和均不大于所有点的标号之和，而仅由可行边组成的完全匹配的边权总和等于所有点的标号之和，故这个匹配是最佳的）。一开始，求出每个点的初始标号：lx[i]=max{e.W|e.x=i}（即每个X方点的初始标号为与这个X方点相关联的权值最大的边的权值），ly[j]=0（即每个Y方点的初始标号为0）。这个初始点标显然是可行的，并且，与任意一个X方点关联的边中至少有一条可行边；
（3）然后，从每个X方点开始DFS增广。DFS增广的过程与最大匹配的匈牙利Hungary算法基本相同，只是要注意两点：一是只找可行边，二是要把搜索过程中遍历到的X方点全部记下来（可以用vst搞一下），以进行后面的修改；
（4）增广的结果有两种：若成功（找到了增广轨），则该点增广完成，进入下一个点的增广。若失败（没有找到增广轨），则需要改变一些点的标号，使得图中可行边的数量增加。方法为：将所有在增广轨中（就是在增广过程中遍历到）的X方点的标号全部减去一个常数d，所有在增广轨中的Y方点的标号全部加上一个常数d，则对于图中的任意一条边(i, j, W)（i为X方点，j为Y方点）：

• <1>i和j都在增广轨中：此时边(i, j)的(lx[i]+ly[j])值不变，也就是这条边的可行性不变（原来是可行边则现在仍是，原来不是则现在仍不是）；
• <2>i在增广轨中而j不在：此时边(i, j)的(lx[i]+ly[j])的值减少了d，也就是原来这条边不是可行边（否则j就会被遍历到了），而现在可能是；
• <3>j在增广轨中而i不在：此时边(i, j)的(lx[i]+ly[j])的值增加了d，也就是原来这条边不是可行边（若这条边是可行边，则在遍历到j时会紧接着执行DFS(i)，此时i就会被遍历到），现在仍不是；
• <4>i和j都不在增广轨中：此时边(i, j)的(lx[i]+ly[j])值不变，也就是这条边的可行性不变。

这样，在进行了这一步修改操作后，图中原来的可行边仍可行，而原来不可行的边现在则可能变为可行边。那么d的值应取多少？显然，整个点标不能失去可行性，也就是对于上述的第<2>类边，其lx[i]+ly[j]>=W这一性质不能被改变，故取所有第<2>类边的(lx[i]+ly[j]-W)的最小值作为d值即可。这样一方面可以保证点标的可行性，另一方面，经过这一步后，图中至少会增加一条可行边。
（5）修改后，继续对这个X方点DFS增广，若还失败则继续修改，直到成功为止；

7.1 分析整个算法的时间复杂度：

每次修改后，图中至少会增加一条可行边，故最多增广M次、修改M次就可以找到仅由可行边组成的完全匹配（除非图中不存在完全匹配，这个可以通过预处理得到），故整个算法的时间复杂度为O(M * (N + 一次修改点标的时间))。

而一次修改点标的时间取决于计算d值的时间，如果暴力枚举计算，这一步的时间为O(M)，

优化：可以对每个Y方点设立一个slk值，表示在DFS增广过程中，所有搜到的与该Y方点关联的边的(lx+ly-W)的最小值（这样的边的X方点必然在增广轨中）。每次DFS增广前，将所有Y方点的slk值设为+∞，若增广失败，则取所有不在增广轨中的Y方点的slk值的最小值为d值。这样一次修改点标的时间降为O(N)，总时间复杂度降为O(NM)。

需要注意的一点是，在增广过程中需要记下每个X、Y方点是否被遍历到，即fx[i]、fy[j]。因此，在每次增广前（不是对每个X方点增广前）就要将所有fx和fy值清空。

O(n^3)的优化：
如果每次都花O(n^2)的时间时间去找 min(lx[i] + ly[j] - mp[i][j])；显然，总的时间复杂度是O(n^3)，这里加一个slack[]数组，记录每次dfs找完美匹配时lx[i] + ly[j] - mp[i][j]的最小值，在实现多次调整时只需要在slack[]里找到调整值d就可以。

匈牙利算法和FF算法结合得到KM算法讲的很详细：二分图匹配之最佳匹配——KM算法
https://www.cnblogs.com/Lanly/p/6291214.html
这个博客讲的太清楚了！
http://www.cppblog.com/MatoNo1/archive/2012/04/26/151724.html

实践： 利用匈牙利算法对目标框和检测框进行关联

在这里我们对检测框和跟踪框进行匹配，整个流程是遍历检测框和跟踪框，并进行匹配，匹配成功的将其保留，未成功的将其删除。

https://blog.csdn.net/zimiao552147572/article/details/105985322

from scipy.optimize import linear_sum_assignment
import numpy as np
from numba import jit
 
@jit
def iou(bb_test, bb_gt):
    """
    在两个box间计算IOU
    :param bb_test: box1 = [x1y1x2y2] 即 [左上角的x坐标，左上角的y坐标，右下角的x坐标，右下角的y坐标]
    :param bb_gt: box2 = [x1y1x2y2]
    :return: 交并比IOU
    """
    xx1 = np.maximum(bb_test[0], bb_gt[0]) #获取交集面积四边形的 左上角的x坐标
    yy1 = np.maximum(bb_test[1], bb_gt[1]) #获取交集面积四边形的 左上角的y坐标
    xx2 = np.minimum(bb_test[2], bb_gt[2]) #获取交集面积四边形的 右下角的x坐标
    yy2 = np.minimum(bb_test[3], bb_gt[3]) #获取交集面积四边形的 右下角的y坐标
    w = np.maximum(0., xx2 - xx1) #交集面积四边形的 右下角的x坐标 - 左上角的x坐标 = 交集面积四边形的宽
    h = np.maximum(0., yy2 - yy1) #交集面积四边形的 右下角的y坐标 - 左上角的y坐标 = 交集面积四边形的高
    wh = w * h #交集面积四边形的宽 * 交集面积四边形的高 = 交集面积
    """
    两者的交集面积，作为分子。
    两者的并集面积作为分母。
    一方box框的面积：(bb_test[2] - bb_test[0]) * (bb_test[3] - bb_test[1])
    另外一方box框的面积：(bb_gt[2] - bb_gt[0]) * (bb_gt[3] - bb_gt[1]) 
    """
    o = wh / ( (bb_test[2] - bb_test[0]) * (bb_test[3] - bb_test[1])
               + (bb_gt[2] - bb_gt[0]) * (bb_gt[3] - bb_gt[1])
               - wh)
    return o
 
"""
利用匈牙利算法对跟踪目标框和yoloV3检测结果框进行关联匹配，整个流程是遍历检测结果框和跟踪目标框，并进行两两的相似度最大的比对。
相似度最大的认为是同一个目标则匹配成功的将其保留，相似度低的未成功匹配的将其删除。
使用的是通过yoloV3得到的“并且和预测框相匹配的”检测框来更新卡尔曼滤波器得到的预测框。
    detections：通过yoloV3得到的检测结果框
    trackers：通过卡尔曼滤波器得到的预测结果跟踪目标框
    iou_threshold=0.3：大于IOU阈值则认为是同一个目标则匹配成功将其保留，小于IOU阈值则认为不是同一个目标则未成功匹配将其删除。
    return返回值：
        matches：跟踪成功目标的矩阵。即前后帧都存在的目标，并且匹配成功同时大于iou阈值。
        np.array(unmatched_detections)：新增目标指的就是存在于detections检测结果框当中，但不存在于trackers预测结果跟踪目标框当中。
        np.array(unmatched_trackers)：离开画面的目标指的就是存在于trackers预测结果跟踪目标框当中，但不存在于detections检测结果框当中。
"""
def associate_detections_to_trackers(detections, trackers, iou_threshold=0.3):
    """
    将检测框bbox与卡尔曼滤波器的跟踪框进行关联匹配
    :param detections:通过yoloV3得到的检测结果框
    :param trackers:通过卡尔曼滤波器得到的预测结果跟踪目标框
    :param iou_threshold:大于IOU阈值则认为是同一个目标则匹配成功将其保留，小于IOU阈值则认为不是同一个目标则未成功匹配将其删除。
    :return:跟踪成功目标的矩阵：matchs。即前后帧都存在的目标，并且匹配成功同时大于iou阈值。
            新增目标的矩阵：unmatched_detections。
                            新增目标指的就是存在于detections检测结果框当中，但不存在于trackers预测结果跟踪目标框当中。
            跟踪失败即离开画面的目标矩阵：unmatched_trackers。
                            离开画面的目标指的就是存在于trackers预测结果跟踪目标框当中，但不存在于detections检测结果框当中。
    """
    """
    1.跟踪器链(列表)：
        实际就是多个的卡尔曼滤波KalmanBoxTracker自定义类的实例对象组成的列表。
        每个目标框都有对应的一个卡尔曼滤波器(KalmanBoxTracker实例对象)，
        KalmanBoxTracker类中的实例属性专门负责记录其对应的一个目标框中各种统计参数，
        并且使用类属性负责记录卡尔曼滤波器的创建个数，增加一个目标框就增加一个卡尔曼滤波器(KalmanBoxTracker实例对象)。
        把每个卡尔曼滤波器(KalmanBoxTracker实例对象)都存储到跟踪器链(列表)中。
    2.unmatched_detections(列表)：
        检测框中出现新目标，但此时预测框(跟踪框)中仍不不存在该目标，
        那么就需要在创建新目标对应的预测框/跟踪框(KalmanBoxTracker类的实例对象)，
        然后把新目标对应的KalmanBoxTracker类的实例对象放到跟踪器链(列表)中。
    3.unmatched_trackers(列表)：
        当跟踪目标失败或目标离开了画面时，也即目标从检测框中消失了，就应把目标对应的跟踪框(预测框)从跟踪器链中删除。
        unmatched_trackers列表中保存的正是跟踪失败即离开画面的目标，但该目标对应的预测框/跟踪框(KalmanBoxTracker类的实例对象)
        此时仍然存在于跟踪器链(列表)中，因此就需要把该目标对应的预测框/跟踪框(KalmanBoxTracker类的实例对象)从跟踪器链(列表)中删除出去。
    """
    # 跟踪目标数量为0，直接构造结果
    if (len(trackers) == 0) or (len(detections) == 0):
        """
        如果卡尔曼滤波器得到的预测结果跟踪目标框len(trackers)为0 或者 yoloV3得到的检测结果框len(detections)为0 的话，
        跟踪成功目标的矩阵：matchs 为 np.empty((0, 2), dtype=int)
        新增目标的矩阵：unmatched_detections 为 np.arange(len(detections))
        跟踪失败即离开画面的目标矩阵：unmatched_trackers 为 np.empty((0, 5), dtype=int)
        """
        return np.empty((0, 2), dtype=int), np.arange(len(detections)), np.empty((0, 5), dtype=int)
 
    """ 因为要计算所有检测结果框中每个框 和 所有跟踪目标框中每个框 两两之间 的iou相似度计算，
        即所有检测结果框中每个框 都要和 所有跟踪目标框中每个框 进行两两之间 的iou相似度计算，
        所以iou_matrix需要初始化为len(detections检测结果框) * len(trackers跟踪目标框) 形状的0初始化的矩阵。 """
    # iou 不支持数组计算。逐个计算两两间的交并比，调用 linear_assignment 进行匹配
    iou_matrix = np.zeros((len(detections), len(trackers)), dtype=np.float32)
    # 遍历目标检测（yoloV3检测）的bbox集合，每个检测框的标识为d，det为检测结果框
    for d, det in enumerate(detections):
        # 遍历跟踪框（卡尔曼滤波器预测）bbox集合，每个跟踪框标识为t，trackers为跟踪目标框
        for t, trk in enumerate(trackers):
            """ 
            遍历每个检测结果框 和 遍历每个跟踪目标框 进行两两之间 的iou相似度计算。
            行索引值对应的是目标检测框。列索引值对应的是跟踪目标框。
            """
            iou_matrix[d, t] = iou(det, trk)
 
    """ 
    row_ind, col_ind=linear_sum_assignment(-iou_matrix矩阵) 
        通过匈牙利算法得到最优匹配度的“跟踪框和检测框之间的”两两组合。
        通过相同下标位置的行索引和列索引即可从iou_matrix矩阵得到“跟踪框和检测框之间的”两两组合最优匹配度的IOU值。
        -iou_matrix矩阵：linear_assignment的输入是cost成本矩阵，IOU越大对应的分配代价应越小，所以iou_matrix矩阵需要取负号。
        row_ind：行索引构建的一维数组。行索引值对应的是目标检测框。
        col_ind：列索引构建的一维数组。列索引值对应的是跟踪目标框。
        比如：
            row_ind：[0 1 2 3]。col_ind列索引：[3 2 1 0]。
            np.array(list(zip(*result)))：[[0 3] [1 2] [2 1] [3 0]]
    """
    # 通过匈牙利算法将跟踪框和检测框以[[d,t]...]的二维矩阵的形式存储在match_indices中
    result = linear_sum_assignment(-iou_matrix)
    matched_indices = np.array(list(zip(*result)))
 
    """ np.array(unmatched_detections)：新增目标指的就是存在于detections检测结果框当中，但不存在于trackers预测结果跟踪目标框当中 """
    # 记录未匹配的检测框及跟踪框
    # 未匹配的检测框放入unmatched_detections中，表示有新的目标进入画面，要新增跟踪器跟踪目标
    unmatched_detections = []
    for d, det in enumerate(detections):
        """ matched_indices[:, 0]：取出的是每行的第一列，代表的是目标检测框。
           如果目标检测框的索引d不存在于匹配成功的matched_indices中每行的第一列的话，代表目标检测框中有新的目标出现在画面中，
           则把未匹配的目标检测框放入到unmatched_detections中表示需要新增跟踪器进行跟踪目标。
        """
        if d not in matched_indices[:, 0]:
            unmatched_detections.append(d)
 
    """ np.array(unmatched_trackers)：离开画面的目标指的就是存在于trackers预测结果跟踪目标框当中，但不存在于detections检测结果框当中 """
    # 未匹配的跟踪框放入unmatched_trackers中，表示目标离开之前的画面，应删除对应的跟踪器
    unmatched_trackers = []
    for t, trk in enumerate(trackers):
        """ matched_indices[:, 1]：取出的是每行的第二列，代表的是跟踪目标框。
           如果跟踪目标框的索引t不存在于匹配成功的matched_indices中每行的第二列的话，代表跟踪目标框中有目标离开了画面，
           则把未匹配的跟踪目标框放入到unmatched_trackers中表示需要删除对应的跟踪器。
        """
        if t not in matched_indices[:, 1]:
            unmatched_trackers.append(t)
 
    """ matches：跟踪成功目标的矩阵。即前后帧都存在的目标，并且匹配成功同时大于iou阈值。
        即把匹配成功的matched_indices中的并且小于iou阈值的[d,t]放到matches中。
    """
    # 将匹配成功的跟踪框放入matches中
    matches = []
    for m in matched_indices:
        """
        m[0]：每行的第一列，代表的是目标检测框。m[1]：每行的第二列，代表的是跟踪目标框。
        iou_matrix[m[0], m[1]] < iou_threshold：
            根据目标检测框的索引作为行索引，跟踪目标框的索引作为列索引，
            即能找到“跟踪框和检测框之间的”两两组合最优匹配度的IOU值，如果该IOU值小于iou阈值的话，
            则把目标检测框放到unmatched_detections中，把跟踪目标框放到unmatched_trackers中。
        """
        # 过滤掉IOU低的匹配，将其放入到unmatched_detections和unmatched_trackers
        if iou_matrix[m[0], m[1]] < iou_threshold:
            unmatched_detections.append(m[0]) #m[0]：每行的第一列，代表的是目标检测框。
            unmatched_trackers.append(m[1])   #m[1]：每行的第二列，代表的是跟踪目标框。
        # 满足条件的以[[d,t]...]的形式放入matches中
        else:
            """ 存储到列表中的每个元素的形状为(1, 2) """
            matches.append(m.reshape(1, 2))
 
    """
    如果矩阵matches中不存在任何跟踪成功的目标的话，则创建空数组返回。
    numpy.concatenate((a1,a2,...), axis=0)：能够一次完成多个数组a1,a2,...的拼接。
    >>> a=np.array([1,2,3])
    >>> b=np.array([11,22,33])
    >>> c=np.array([44,55,66])
    >>> np.concatenate((a,b,c),axis=0)  # 默认情况下，axis=0可以不写
    array([ 1,  2,  3, 11, 22, 33, 44, 55, 66]) #对于一维数组拼接，axis的值不影响最后的结果
    """
    # 初始化matches,以np.array的形式返回
    if len(matches) == 0:
        matches = np.empty((0, 2), dtype=int)
    else:
        """ 
        np.concatenate(matches, axis=0)：
            [array([[0, 0]], dtype=int64), array([[1, 1]], dtype=int64),  。。。] 转换为 [[0, 0] [1, 1] 。。。]
        """
        matches = np.concatenate(matches, axis=0) # 默认情况下，axis=0可以不写
 
    return matches, np.array(unmatched_detections), np.array(unmatched_trackers)

多目标跟踪，即MOT（Multi-Object Tracking），也就是在一段视频中同时跟踪多个目标

初始化问题

https://blog.csdn.net/zimiao552147572/article/details/105941324

多目标跟踪问题中并不是所有目标都会在第一帧出现，也并不是所有目标都会出现在每一帧。那如何对出现的目标进行初始化，可以作为跟踪算法的分类表针。

目标跟踪的常见的分类方法

常见的初始化方法分为两大类，一个是Detection-Based-Tracking(DBT),一个是Detection-Free-Tracking(DFT)。下图比较形象地说明了两类算法的区别。

DBT

DBT的方式就是典型的tracking-by-detection模式，即先检测目标，然后将目标关联进入跟踪轨迹中。那么就存在两个问题，第一，该跟踪方式非常依赖目标检测器的性能，第二，目标检测的实质是分类和回归，即该跟踪方式只能针对特定的目标类型，如：行人、车辆、动物。DBT则是目前业界研究的主流。

DFT

DFT是单目标跟踪领域的常用初始化方法，即每当新目标出现时，人为告诉算法新目标的位置，这样做的好处是target free，坏处就是过程比较麻烦，存在过多的交互，所以DBT相对来说更受欢迎。

处理模式

MOT也存在着不同的处理模式，Online和Offline两大类，其主要区别在于是否用到了后续帧的信息。下图形象解释了Online与Offline跟踪的区别。
Online Tracking

Online Tracking是对视频帧逐帧进行处理，当前帧的跟踪仅利用过去的信息。

Offline Tracking

不同于Online Tracking，Offline Tracking会利用前后视频帧的信息对当前帧进行目标跟踪，这种方式只适用于视频，如果应用于摄像头，则会有滞后效应，通常采用时间窗方式进行处理，以节省内存和加速。

运动模型

为了简化多目标跟踪的难度，我们引入运动模型类简化求解过程，运动模型捕捉目标的动态行为，它估计目标在未来帧中的潜在位置，从而减少搜索空间。

跟踪方法

多目标跟踪中基于神经网络的算法，端到端的算法并不多，主要还在实验室的刷榜阶段，模型复杂，速度慢，追踪结果也不好，我们就不再介绍，主要给大家介绍以下两种主流的算法：

基于Kalman和KM算法的后端优化算法

该类算法能达到实时性，但依赖于检测算法效果要好，特征区分要好（输出最终结果的好坏依赖于较强的检测算法，而基于卡尔曼加匈牙利匹配的追踪算法作用在于能够输出检测目标的id，其次能保证追踪算法的实时性），这样追踪效果会好，id切换少。代表性的算法是SORT/DeepSORT。

SORT 是一种实用的多目标跟踪算法，引入了线性速度模型与卡尔曼滤波来进行位置预测，在无合适匹配检测框的情况下，使用运动模型来预测物体的位置。匈牙利算法是一种寻找二分图的最大匹配的算法，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。而卡尔曼滤波可以看作是一种运动模型，用来对目标的轨迹进行预测，并且使用确信度较高的跟踪结果进行预测结果的修正。

多目标追踪一般接在目标检测后。在工业界目标检测采用比较多的是yolo检测网络****，单阶段式，速度快，精度不差，部署在NV的平台帧率可以达到30fps以上。所以要实现目标检测代码和多目标追踪代码集成的任务，需要先将两者的框架统一。先实现目标检测网络，检测的输出结果主要是将检测框的位置信息输入到多目标追踪算法中。

基于多线程的单目标跟踪的多目标跟踪算法

这类算法特点是跟踪效果会很好，因为其为每一类物体都单独分配了一个跟踪器。但该算法对目标尺度变化要求较大，参数调试需要合理，同时该算法极耗cpu资源，实时性不高，代表算法是利用KCF进行目标跟踪。

多目标追踪本质上是多个目标同时运动的问题，所以有提出将单目标跟踪器引入到多目标追踪的问题，为每一个目标分配一个跟踪器，然后间接地使用匹配算法来修正那些跟踪失败或新出现的目标。代表性的单目标跟踪算法为核相关滤波算法（KCF）,在精度和速度上能够同时达到很高的水平，是当时单目标跟踪最优秀的算法之一，后来的很多单目标跟踪算法都是基于此做的改进。

实际应用过程中会为每个目标分配一个KCF跟踪器并采用多线程的方式来组织这些跟踪器。同时因为实际硬件条件的限制，不可能提供强大的计算力资源，会采用检测器与跟踪器交替进行的跟踪策略。由于检测的帧率不高，使得跟踪的维持效果出现滞后或框飘的现象较为严重，实用性不大。