台大机器人学——03 机械臂描述及其顺向运动学

PS: 本篇文章为台大机器人学学习笔记，B站视频链接如下：
https://www.bilibili.com/video/BV1v4411H7ez?p=7

0. 引言

• 运动学：关于运动状态本身，不讨论到力，关于位置、速度、加速度、时间等的关系。
• 动力学：力/力矩如何产生运动
• 机械臂：
  多个杆件(link)相串联，杆件间可以相对运动或者转动，由制动器驱动完成
  对应关系描述：描述臂的末端点状态（位置，速度…）
  连接方式：${}^{W}P=f({\theta }_1,{\theta }_2,...,{\theta }_n)$
  描述方法：找出各个杆件间的相对几何状态，在各个杆件上建立frame，以其状态来表述

1. 机械臂描述方式

• 关节（joint）：
  每个关节具有1自由度，每个关节绕着特定的轴（axis）进行转动或者移动

• 杆件（link）: 连接关节
  

• 两个关节间描述：
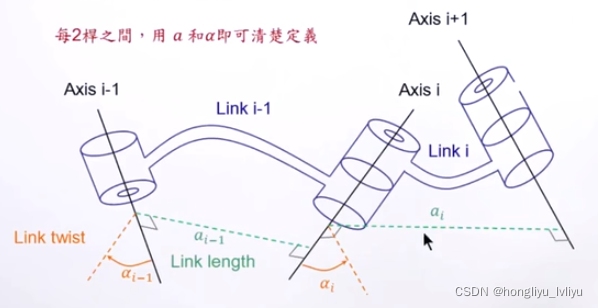
  对于每个关节与其连接的杆件，可以其连接方向进行连续的定义，例如图中标号$i-1$的关节与杆件以及标号为$i$的；每个关节对应的转轴可以为任意方向：
  ① 两个转轴之间有一线段（$a_{i-1}$）与两个转轴都垂直；
  ② 还需要一个角度来描述转轴之间的转动关系（${\alpha }_{i-1}$）
  每两个杆之间，用$a,\alpha$即可定义
  

• 多个关节间描述：
  如果需要多杆串联，则还需要另外两个参数来描述相邻线段$a_{i-1}$与$a$之间的相对几何关系
  ① 轴垂直线段$a_{i-1}$与$a$之间的相对距离：$d_i$
  ② 轴垂直线段$a_{i-1}$与$a$之间的转角关系：${\theta }_i$
  

–> 针对每个杆件，需要四个参数描述其状态：$({\alpha }_i,a_i,d_i,{\theta }_i)$

根据轴的功能不同，移动与转动的轴，够各自只有一个参数在变化：
以axis i 为例：

转动	移动
${\theta }_i$变化，其它参数固定	$d_i$变化，其它参数固定

2. DH表达法（denavit-hartenberg）

• 如何在杆件上建立坐标系：
  

${\hat{Z}}_i$	${\hat{X}}_i$	${\hat{Y}}_i$
转动/移动关节的转轴方向	当$a_i$≠0：沿着$a_i$的方向	遵循右手定则，与${\hat{Z}}_i$ 和${\hat{X}}_i$两者垂直
	$a_i=0$（即${\hat{Z}}_i$ 与${\hat{Z}}_{i+1}$ 相交）：则取${\hat{X}}_i$ 与${\hat{Z}}_i$ 和${\hat{Z}}_{i+1}$两者垂直（如下图）

• 地杆（第0杆）的特别表述：
  由于link(0)固定，条件相对少，较为特殊，对于link(0)可以有特别的表述方式

令frame(0) 与 frame(1)重合：

	${\alpha }_0$	$a_0$	$d_1$	${\theta }_1$
转动	0(令frame(0) 与 frame(1)重合)	0(令frame(0) 与 frame(1)重合)	0	任意
移动	0(令frame(0) 与 frame(1)重合)	0(令frame(0) 与 frame(1)重合)	任意	0

• 任意杆件link(n)的表述：

取与${\hat{X}}_{n-1}$同方向：

	${\alpha }_n$	$a_n$	$d_n$	${\theta }_n$
转动	0	0	0	任意
移动	0	0	任意	0

• DH表达法（denavit-hartenberg）
  
  统一规律(注意下标)：

	${\alpha }_{i-1}$	$a_{i-1}$	$d_i$	${\theta }_i$
方向	以${\hat{Z}}_{i-1}$方向看	沿${\hat{X}}_{i-1}$方向	以${\hat{Z}}_{i-1}$方向看	沿着${\hat{Z}}_{i-1}$方向
含义	${\hat{Z}}_{i-1}$与${\hat{Z}}_i$夹角	${\hat{Z}}_{i-1}$与${\hat{Z}}_{i-1}$间的距离（$a_i>0$）	${\hat{X}}_{i-1}$和${\hat{X}}_i$夹角	${\hat{X}}_{i-1}$和${\hat{X}}_{i-1}$间的距离

3. 杆件的坐标转换

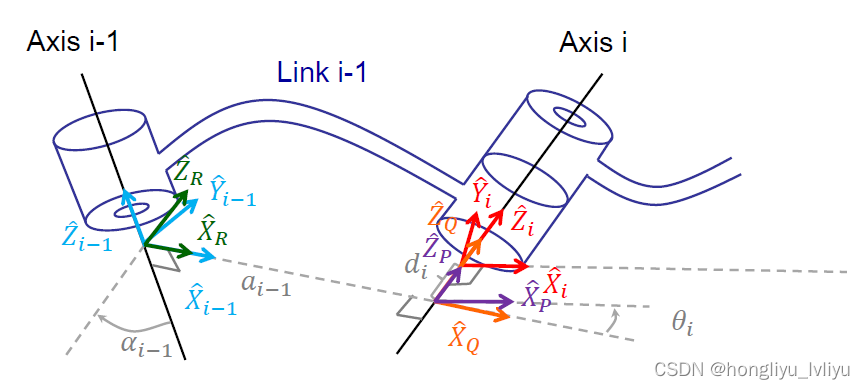
根据转轴间由四个参数来表达的特点，分成四步进行转换，得到：

$${}_i^{i-1}T=T_{{\hat{X}}_{i-1}}({\alpha }_{i-1})T_{{\hat{X}}_R}(a_{i-1})T_{{\hat{Z}}_Q}({\theta }_i)T_{{\hat{Z}}_P}(d_i)$$

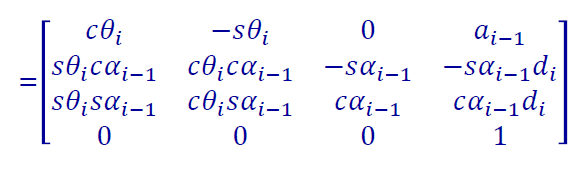
• 对于连续的link，有：

$${}_n^{0}T={}_1^{0}T{}_2^{1}T...{}_{n-1}^{n-2}T{}_n^{n-1}T$$
frame{n} 相对于 frame{n} 的空间几何关系可以清晰表达；
在 frame{n} 下表达的向量，可以转回 frame{0} 下进行表达。

• 示例1：
  
  $Z$轴为转轴方向（垂直与纸面）；
  $X$轴为与两个转轴垂直的一线段方向；
  $Y$轴根据$Z、X$轴右手定则确定；

对于 frame{0}：
选择坐标系与 frame{1} 重合，但取${\theta }_0=0$，在 frame{1} 转动角度为0时，frame{1} 与 frame{0} 重合。
对于 frame{3}（ frame{n}）：
也选择杆件的方向，在${\theta }_3=0$时，与杆件2 方向重合。

四个参数列表如下：

由于在此范例中，转轴都是相互平行，垂直于纸面的，因此多数参数为0.

机械臂末端点$P$ 在frame{3} 下的坐标为：
3 P = { L 3 , 0 , 0 } {}^{3}P=\{L_{3},0,0\} 3P={L3​,0,0}
如果想知道末端点$P$ 在frame{0} 下（相对地面）的坐标则可以进一步进行转化。

- 示例2：

分析流程：
① 分析转动移动，找到转轴方向

1转动，2移动，3转动

② 找与两两转轴向垂直的线段$a$
转轴1、2垂直相交，线段a即为两转轴的交点；
转轴2、3重合，也以一点作为基准。

③ 按照方法建立各个转轴（先不定义地杆与最后一杆）的坐标系
其中${\hat{X}}_1,{\hat{X}}_2$定义为往前或往后都可以

④ 建立frame(0) , frame(n) 的坐标系
frame(0) 与frame(1) 重合且选择$\theta =0$的位置
frame(3) （即frame(n)）选择相对于frame(2) 角度为0的时候

⑤ 可以列出各个坐标系之间的四个参数关系

其中90°为${\hat{Z}}_1$转到${\hat{Z}}_2$；
$a$都为0：根据②中的分析，转轴都重合在某点，所以都为0；
$d$根据图示，可以看出坐标系之间转轴的距离；

⑥ 机械臂末端分析
$P$点对于frame{3}来说，其坐标为：
3 P = { 0 , 0 , L 3 } {}^{3}P=\{0,0,L_{3}\} 3P={0,0,L3​}
可以通过转换将$P$点坐标转换到frame{0}

• PS：对于转轴相交时的讨论：
  
  当${\hat{Z}}_1$与${\hat{Z}}_2$相交时，${\hat{Z}}_2$的方向有两个选择，${\hat{X}}_1$的方向有两个选择。

4. 坐标系转换

顺向运动学：
即先找到各个关节之间的关系，再得到末端与机械臂之间的关系（由$\theta$到${}^{W}P$）。

逆向运动学：
先知道末端在世界坐标系下的表达，再得到各个关节的关系。

cartesian space：
末端点在世界坐标系下的表达

joint space：
关节坐标系下的表达

actuator space：
在某些情况下，关节的表达与执行机构相关