hash function/ hash table 背后的数学基础

原文请见：Load Balancing and the Power of Hashing

如果你参加一次软件工程师的面试并你被问到一个很难的有关算法的题目，那么你最好考虑使用散列函数（hash tables）？更简洁地说吧：谷歌喜欢散列函数（and BAT）。要想知道为什么散列函数如此有用，你多少应该知道它里面的数学。

一些概念术语的阐述

• load factor（装填因子）

  n keys, m slots（键与槽） ⇒ $\alpha=\frac nm$, average # keys per slot

• Expected unsuccessful search time（失败搜索（搜索的数据不在表中）的时间期望）

  $\Theta(1+\alpha)=\Theta(1+\frac nm)$

  1：hash and accessing the slot

  $\alpha$：the cost of the searching the list.

• Expected search time == $\Theta(1)$ if $n==\Theta(m)$（不会超过 $m$ 的整数倍）

• division method：

  $h(k)=k\mod m$

• multiplication method：

  $m=2^r$，$w$表示计算机的位数（之所以更推荐乘法，是因为计算机更擅长乘法，此时考虑计算机的位数，可见这时就牵涉计算机硬件体系结构的问题了）

  $h(k)=(A\cdot k \mod 2^w)>> (w-r)$

  $A$ 是位于 $[2^{w-r},2^w]$之间的一个奇数，且不接近于 $2^{w-1}$ 或者 $2^{w}$。

  我们不妨来分析这一hash函数式，$A\cdot k \mod 2^w$ 共保留 $w$ 位，再右移 $w-r$，保留中间的 $w-(w-r)==r$ 位，也正是最终得到的槽（slots）的个数，这一切都很convenient，对计算机而言。

  我们来举一个实例，取 $r=3,w=7,A=0b1011001$（7位的计算机，:-D），当 $k=0b1101011$ 时，$A\cdot k=0b10010100110011$，再进行取模运算，也即保留最后的 $w=7$位，$A\cdot k \mod 2^w$ 得 $0b0110011$，最后右移 $w-r=7-3=4$ 位，即保留 $0b011=3$，也即 $h(k)=3$。

开地址法的分析

首先我们需要一个均匀哈希的假设（Assumption of uniform hashing）：each key equally likely to have any one of the $m!$ perms as its probe seq，independence of other keys.

Theorem：$E\left [ \# \textrm{probes}\right ]\leq \frac1{1-\alpha}$，if $\alpha<1$（也即 $n<m$）

Pf (unsucc search)：
1 probe always necessary with prob $\frac nm$ collision, ⇒ 2nd probe necessary, $\frac{n-1}{m-1}$ collision ⇒ 3nd, $\frac{n-2}{m-2}$

注意到 $\frac{n-i}{m-i}<\frac nm=\alpha$

$$\begin{split} E\left [ \# \textrm{probes}\right ]=&1+\frac nm(1+\frac{n-1}{m-1}(1+\frac{n-2}{m-2}(\cdots(1+\frac1{m-n+1})\cdots)))\\ \leq&\; 1+\alpha(1+\alpha(1+\alpha(\cdots (1+\alpha) \cdots)))\\ \leq&\;1+\alpha+\alpha^2+\alpha^3+\cdots\\ =&\sum_{i=0}^\infty \alpha^i\\ =&\frac1{1-\alpha} \end{split}$$
当 $\alpha<1$ 且为常数时，共需要 $\Theta(1)$ 次探测；

• $\alpha=0.5$ ⇒ 2次
• $\alpha=0.9$ ⇒ 10次

$\alpha$ 不能太大，也即 hash table 不能太稠密；

universal hashing（全局哈希）

Idea is：choose hash function at random independen t from keys，这正是所谓的 universal hashing（全域hash）

Def：
$U$ 为键的全域（a universe of key）
$H$ 为哈希函数的有限集（a finite collection of hash functions）将 $U$ 映射到 $\{0, 1, 2,\ldots,m-1\}$

$H$ is universal if $\forall x,y\in U, \text{where }x\neq y, |\{h\in H,h(x)=h(y)\}|=\frac{|H|}m$（全域的定义），$|\{h\in H,h(x)=h(y)\}|$表示的是 hash function 的数目，也即 $\frac{|H|}m$表示的不是概率而是某一集合的大小，如下图所示：

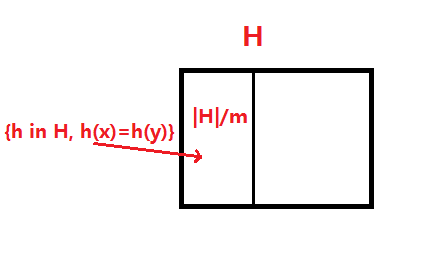
则从 $H$ 中随机地选择一个 hash function $h$（我们是随机地选择 hash function，而不是随机地选择keys），发生 $h(x)=h(y)$的概率为 $\frac{|H|/m}{|H|}=\frac1m$

Thm. Choose $h$ randomly from $H$, suppose we’re hashing $n$ keys into $m$ slots in Table $T$, for given key $x$, the expected number of collisions with $x$:

$$E\left [\# \text{collisions with }x\right ]<\frac nm$$

Pf. Let $C_x$ be r.v. denoting total（概率分析中常用到的一种手段，将某个total型的随机变量转换为一系列指标随机变量的总和） collisions of keys in T with $x$, 定义如下的指标随机变量：

$$\begin{split} C_{xy}= \left \{ \begin{array}{ll} 1,& h(x)=h(y)\\ 0,& \text{otherwise} \end{array} \right. \end{split}$$

$E(C_{xy})=\mathrm{Pr}(h(x)=h(y))=\frac1m$，$C_x=\sum\limits_{y=T-\{x\}}C_{xy}$：

$$E(C_x)=E(\sum_{y=T-\{x\}}C_{xy})=\sum_{y=T-\{x\}}E(C_{xy})=\frac{n-1}m$$

构造全局哈希

此构造对 $m$ 为质数时有效，将键 $k$ 分解为 $r+1$ 位，$k=<k_0,k_1,\ldots,k_r>, \text{where } 0\leq k_i \leq m-1$。（这种分解的思想在于，把 $k$ 用某种m进制表示）

构造我们的随机化策略（randomized strategy）。
随机化的对象是对哈希函数的选择。

选择 $a=<a_0,a_1,\ldots,a_r>$，each $a_i$ is chosen randomly from $[0,m-1]$（也即每一 $a_i$ 都是 $m$ 进制）.

最终，我们定义 $h_a(k)=(\sum\limits_{i=0}^r a_ik_i)\mod m$，而 $\sum\limits_{i=0}^ra_ik_i$又可通过向量内积的形式得以计算，所以此时的全域 $H$有多大，$|H|=m^{r+1}$，每一位的取值为$[0,m-1]$（$m$ 种可能），共 $r+1$位；

Thm：此时的 $H$是全域的。也即需证明 $|\{h\in H,h(x)=h(y)\}|=\frac{|H|}m$（$x$与 $y$互异）。注：同一个 hash function $h(\cdot)$，或者写作 $h_a(\cdot)$，对不同的两个 key $x,y$，映射到相同的槽slot，这样的哈希函数的个数。

证明：
分别将 $x, y$ 分解，得$x=<x_0,x_1,\ldots,x_r>$，$y=<y_0,y_1,\ldots,y_r>$，$x$ 与 $y$ 互异，如果$x\neq y$，则 <x0,x1,…,xr> <script id="MathJax-Element-98" type="math/tex"> </script>比与 <y0,y1,…,yr> <script id="MathJax-Element-99" type="math/tex"> </script>在某位（至少一位）不同，不失一般性的，设该位为0，此时问有多少个 $h_a\in H$会使得 $x$与 $y$ 发生碰撞。
也即：

$$h_a(x)=h_a(y)\\ \Downarrow\\ \sum_{i=0}^ra_ix_i\equiv \sum_{i=0}^ra_iy_i \pmod m\\ \Downarrow\\ \sum_{i=0}^ra_i(x_i-y_i)\equiv 0 \pmod m\\ \Downarrow\\ a_0(x_0-y_0)+\sum_{i=1}^ra_i(x_i-y_i)\equiv 0 \pmod m\\ \Downarrow\\ a_0(x_0-y_0)\equiv -\sum_{i=1}^ra_i(x_i-y_i)\pmod m$$

因为 $x_0\neq y_0$，所以 $x_0-y_0$ 的逆元，也即 $(x_0-y_0)^{-1}$ 一定存在，所以：

$$a_0\equiv \left (-\sum_{i=1}^ra_i(x_i-y_i)\right ) \cdot (x_0-y_0)^{-1} \pmod m$$

也即，$a_0$ 完全由 $a_i,i=1,\ldots,a_r$ 决定，或者说任何 $a_i,i=1,2,\ldots,r$ 都存在一个 $a_0$，使得 $h_a(x)\equiv h_a(y)$（发生碰撞），也即自由度为 $(1+r)-1=r$。

$$\# \left [h_a(x)\equiv h_a(y)\right ]=\underbrace{m\cdot m\cdots m}_r=m^r=\frac{|\mathcal H|}m$$