深度学习一：神经网络基础

1. 线性回归和逻辑回归

• 线性回归 用于帮助预测一个连续范围；
• 逻辑回归 其实不是回归算法，而是一个分类算法，是一个用于二分分类的算法。二分分类是指我们的分类结果标签只有两个。

比如，以下两个实例，就分别为回归问题和分类问题：

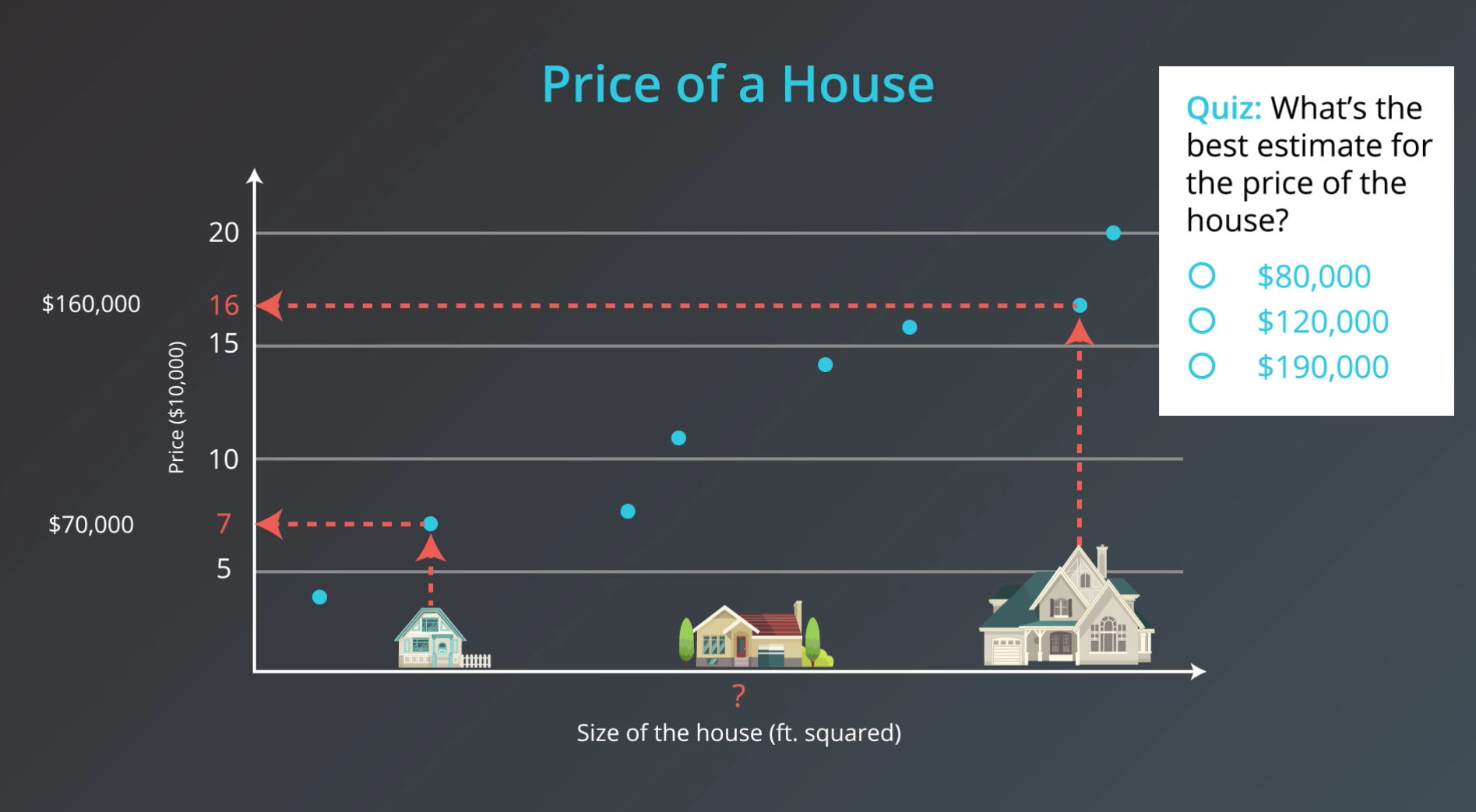
2. 感知机算法

2.1 感知机定义

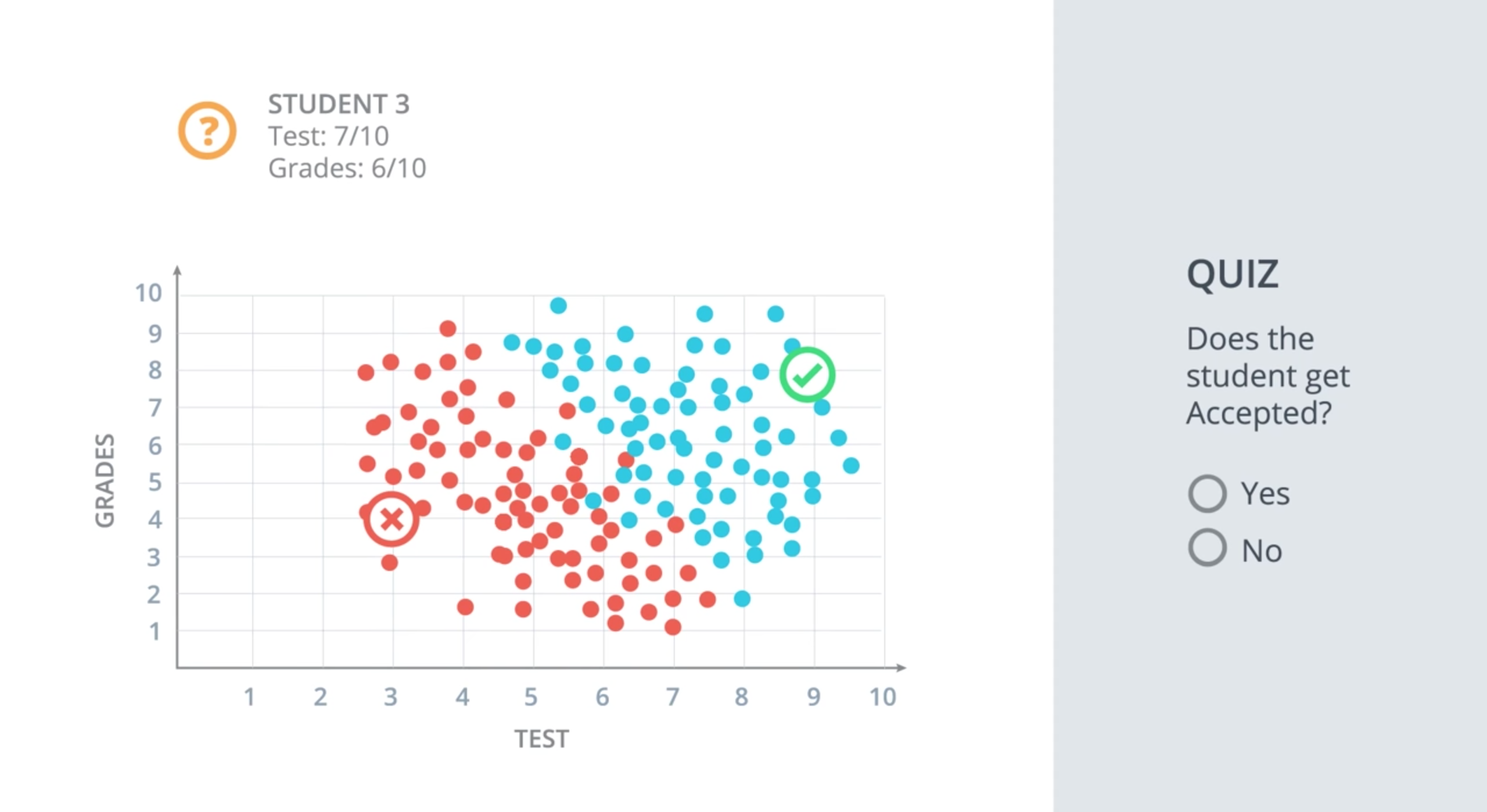
我们先来看一个分类的例子：假设我们是一所高校的招生人员，工作就是接受或拒绝申请的学生，我们可以利用两方面的信息来评估这些学生，它们分别是，考试成绩 和 在校期间的平时成绩。我们有一些之前同学被录取的数据，现在想知道一名考试得了 7 分(满分 10 分)、平时成绩 $6$ 分(满分 $10$ 分)的学生是否被录取？

这个例子就像下图中，考试成绩为 $x_1$，在校期间的平时成绩为 $x_2$，我们也可以有其他变量，诸如论文成绩等，最终得到学生是否被录取的结果，这就是感知机。

感知机(perceptron) 可以看作节点的组合，即这些单独的节点被称为 感知机。下图中第一个节点计算线性方程式和权重上的输入后，第二个节点把 阶跃函数(Step Function) 应用到结果中：

现在已经看到了一个简单的神经网络的，是如何做出决策的：接收输入数据—>处理该信息(感知机)—>以决策的形式产生输出(激活函数(activation function))。

其中，权重(weight) 帮助了解哪些信息在做出一个决定时更为重要。它取决于神经网络自己去学习哪些数据是最重要的，并调整它如何考虑这些数据。

2.2 多层感知机

先来看看逻辑运算符的感知机，诸如 AND、OR、NOT，使用单层感知机就可以将这些逻辑运算符表示为感知机：

现在问题来了，如果下面这种类似 XOR 逻辑运算符，这四个点似乎很难用一条支线分开，那么是否还能将这种运算转换为感知机呢？
答案是可以的，大致的思路概括起来就是：我们将组合使用多个感知器，一个感知器的输出作为另一感知器的输入，这样就形成了多层感知器的结构--------这种结构称之为神经网络。

2.3 感知机算法

1. 由随机权重开始：$w_1,...,w_n,b$
2. 对于每一个误分类的点 $(x_1,...,x_n)$:
   2.1 如果prediction=0，意味着一个 positive 的点在 negative 的区域: 对于 $i=\mathrm{1...}n$，更新：
   $w_i=w_i+\alpha x_i$，其中 $\alpha$ 为学习率 。
   $b=b+\alpha$----将线向误匹配点移动。
   2.2 如果prediction=1，意味着一个 negative 的点在 positive 的区域: 对于 $i=\mathrm{1...}n$，更新：
   $w_i=w_i-\alpha x_i$，其中 $\alpha$ 为学习率。
   $b=b-\alpha$----将线向误匹配点移动。
3. 重复步骤二直到零误差或者一个固定误差亦或者重复了固定次数

3. 误差函数

现在对误差函数做一个形象的比喻，假设站在一座山上，称之为误差之巅。我们想尽快下山，下山的方式是看看周围，考虑所有下山的可能方向，然后选择一个下降高度最多的方向-----然后朝着这个方向迈出一步，高度降低了，而后不断重复这一过程，我们始终在降低高度，直至完全下山将误差降至最低。将高度作为误差，可以告诉我们目前的状况与理想解决方案的差别有多大--------这种方法叫做梯度下降。

现在用上面的示例来告诉计算机，现在距离完美的解决方案还有多远：

这里有两个错误，这是我们的高度，也就是误差，就像是下山一样，我们会朝着所有方向看去，看看如何移动直线，以便降低误差-------在这种方法中会有一个问题：每一个方向的梯度都是一样的，不知道该如何操作。
另一方面，在误差之巅，我们可以得到高度的小幅变化，知道哪个方向下降最多。

因此，误差函数不能是离散的，而必须是连续的------不能以跳跃形式从 2 到 1 而后从 1 到 0。也就是说误差函数必须是可微分的。

综上，要做的是，构建一个连续误差函数，比如上方的六个点，其中四个分类正确，另外两个分类错误。误差函数将向这两个分类错误的点分配大的惩罚值，并为四个分类正确的点分配小的惩罚值。当点分类错误时，惩罚值约等于点离直线的距离，当点分类正确时，则约等于0。现在通过将所有点的误差相加得到总误差，两个分类错误的点使误差增大了很多。因此需要移动直线，以便降低该误差。现在可以实现误差函数的连续变化了，我们可以对直线参数进行小改动，可以使误差函数也产生一个小的变化。

如果移动直线，可以看到某些点的误差降低了；另一些稍微增大了，但是对于它们的总和来说是变小了，因为现在两个分类错误的点分类正确了。

假如上面这些点代表学生，离散算法将告诉我们学生是录取了还是被拒了，用0表示被拒，用1表示被录取；另一方面，点离黑线越远，它的概率就越大。完全位于蓝色区域的点概率很高，完全位于红色区域的点概率就很低。位于直线上的点都有50%的概率位于蓝色区域。可以看出，概率是关于点离直线距离的函数。
从离散到连续预测的方法是，将激活函数从左侧的阶跃函数，变成右侧的 s 函数：
概率空间如下：

可以看出，点位于中央直线时 $Wx+b=0$，意味着 $\sigma (Wx+b)$ 刚好是 0.5。

左图是原来的感知机，激活函数是阶跃函数；右侧是新的感知机，激活函数是 s 函数。新的感知机，接收输入数据后，将数据乘以箭头边上所示的权重，并将结果相加，然后应用 s 型函数。得到的结果不再是之前那样的 1 或 0，而是返回一个介于 0 到 1 之间的值。所以之前说的是学生是否被录取，现在说的是学生被录取的概率有多大。

2.1 Softmax 函数

假设我们有 n 类和线性模型，可以得到以下分数：$Z_1,...,Z_n$，每个分数代表一个类别。我们要把它们转换成概率，此时对象的概率为：
$$P(clas{s}_i)=\frac{e^{Zi}}{e^{Z1}+...+e^{Zn}}$$

3. One-Hot Encoding

如果输入变量有很多类该怎么处理？如同一变量有三个类别，也许我们可以输入0,1和2，但这很明显是错误的，因为这假定了各类之间的依赖性，而实际上我们没有这种关系。我们要做的是为每个分类提供一个变量。如下图所示，每个都有对应的一列：

如果输入是鸭子，鸭子的变量是1，海狸和海象的变量是0；对于海狸和海象也是如此。我们可以有多列数据，不过至少它们没有必要的依赖关系，这个过程叫做 One-Hot 编码，在处理数据时得到广泛应用。

4. Cross Entropy

继续使用上述示例，比较模型好坏的方法，最简单的是根据计算出的每个点出现所示颜色的概率，将这些概率相乘，以便获得整个模型的概率。通过计算可以看出，右侧模型的概率比左侧高得多，现在只需最大化这一概率。但是概率是数字的乘积，而乘积很难计算。

因此，我们想到了使用对数，因为对数具有良好的特性，即 $log(ab)=log(a)+log(b)$。要注意的是，0-1 之间数字的对数都是负值，因为对 1 取负值才能得到 0。所以，概率的对数都是负值，对它取相反数是行得通的，这样会得到正数。我们要做的就是，对得到的概率的对数的相反数进行求和，称之为交叉熵。

可以看到，左侧错误的模型的交叉熵是4.8，这非常高，而右侧的更优的模型交叉熵较低，是1.2，准确的模型可以让我们得到较低的交叉熵。

一直计算出的概率与误差负相关，如果我们计算出概率，并且得到每个点所对应的对数值，我们实际上得到了每个点的误差。分类正确点的误差较小，而分类错误点的误差较大，交叉熵可以告诉我们模型的好坏。所以目标从最大化概率转变为最小化交叉熵。

上图的交叉熵是有两类时的情况，如果门后有礼物 $y=1$，如果没有 $y=0$。

而如果有多个类别呢？

其中 $m$ 是分类的数量。

5. 误差函数

误差函数与交叉熵想死，但是加上了平均：

既然通过 sigmoid 线性函数 $wx+b$ 得到了 $\widehat{y_i}$ 的概率，那么整个误差公式实际上是 $w$ 和 $b$ 作为模型的权重：
$$\begin{array}{l}ErrorFunction=-\frac{1}{\mathrm{m}}{\sum }_{\mathrm{i}=1}^{\mathrm{m}}\left(1-{\mathrm{y}}_1\right)\left(\ln \left(1-{\hat{y}}_i\right)\right)+{\mathrm{y}}_i\ln \left({\hat{y}}_i\right)\\ \\ \mathrm{E}(\mathrm{W},\mathrm{b})=-\frac{1}{\mathrm{m}}{\sum }_{i=1}^{\mathrm{m}}\left(1-y_i\right)(\ln \left(1-\sigma \left(\mathrm{W}{\mathrm{x}}^{(i)}+\mathrm{b}\right)\right)+{\mathrm{y}}_i\ln (\sigma \left(\mathrm{W}{\mathrm{x}}^{(\mathrm{i})}+\mathrm{b}\right)\end{array}$$

6. 梯度下降法

在知道了误差函数之后，可以开始着手于找到最小的误差节点了。现在误差函数 $E$ 的输入是 $w_1$ 和 $w_2$，因此 $E$ 的梯度是对 $w_1$ 和 $w_2$ 做偏导的向量和。这个导数实际告诉我们要移动的方向，以最大化增加误差函数。因此，如果我们取梯度的反方向，这就是最小化误差的方向。
重复上述步骤，直到到达最低点。

6.1 梯度下降法公式

推导之前，有一点值得关注，那就是 sigmoid 函数有一个很方便的导数：
$$\begin{array}{rl}{\sigma }^{\prime }(x)& =\frac{\partial }{\partial x}\frac{1}{1+e^{-x}}\\ & =\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}\\ & =\frac{1}{1+e^{-x}}\cdot \frac{e^{-x}}{1+e^{-x}}\\ & =\sigma (x)(1-\sigma (x))\end{array}$$

现在，我们有 $m$ 个标记了的点：$x^{(1)},x^{(2)},...,x^{(m)}$，误差函数为：
$$E=-\frac{1}{m}\sum _{i=1}^m\left(y_i\ln \left({\hat{y}}_i\right)+\left(1-y_i\right)\ln \left(1-{\hat{y}}_i\right)\right)$$

其中，${\hat{y}}_i=\sigma \left(W{x}^{(i)}+b\right)$：

我们的目标，是在点 $x=(x_1,...,x_n)$ 计算 $E$ 的梯度，由偏导给出：
$$\nabla E=\left(\frac{\partial }{\partial w_1}E,\cdots ,\frac{\partial }{\partial w_n}E,\frac{\partial }{\partial b}E\right)$$

每个点所产生的误差可以简单的写成：
$$E=-y\ln \left(\hat{y}\right)+\left(1-y\right)\ln \left(1-\hat{y}\right)$$

为了计算误差相对于权重的导数，我们先计算 $\frac{\partial }{\partial w_j}\hat{y}$，给定 $\hat{y}=\sigma (Wx+b)$:
$$\begin{array}{rl}\frac{\partial }{\partial w_j}\hat{y}& =\frac{\partial }{\partial w_j}\sigma (Wx+b)\\ & =\sigma (Wx+b)(1-\sigma (Wx+b))\cdot \frac{\partial }{\partial w_j}(Wx+b)\\ & =\hat{y}(1-\hat{y})\cdot \frac{\partial }{\partial w_j}(Wx+b)\\ & =\hat{y}(1-\hat{y})\cdot \frac{\partial }{\partial w_j}\left(w_1{x}_1+\cdots +w_j{x}_j+\cdots +w_n{x}_n+b\right)\\ & =\hat{y}(1-\hat{y})\cdot x_j\end{array}$$

由此可得：
$$\begin{array}{rl}\frac{\partial }{\partial w_j}E& =\frac{\partial }{\partial w_j}[-y\log (\hat{y})-(1-y)\log (1-\hat{y})]\\ & =-y\frac{\partial }{\partial w_j}\log (\hat{y})-(1-y)\frac{\partial }{\partial w_j}\log (1-\hat{y})\\ & =-y\cdot \frac{1}{\hat{y}}\cdot \frac{\partial }{\partial w_j}\hat{y}-(1-y)\cdot \frac{1}{1-\hat{y}}\cdot \frac{\partial }{\partial w_j}(1-\hat{y})\\ & =-y\cdot \frac{1}{\hat{y}}\cdot \hat{y}(1-\hat{y})x_j-(1-y)\cdot \frac{1}{1-\hat{y}}\cdot (-1)\hat{y}(1-\hat{y})x_j\\ & =-y(1-\hat{y})\cdot x_j+(1-y)\hat{y}\cdot x_j\\ & =-(y-\hat{y})x_j\end{array}$$

一个相似的计算可以得到：
$$\frac{\partial }{\partial b}E=-(y-\hat{y})$$

总结，梯度为：
$$\nabla E=-(y-\hat{y})(x_1,...,x_n,1)$$

6.2 梯度下降步骤

因此，由于梯度下降步骤只是简单地在每一点减去误差函数的梯度的倍数，那么这将以以下方式更新权值:
$$w_i^{\prime }\leftarrow w_i-\alpha \left[-(y-\hat{y})x_i\right]$$

等价于：
$$w_i^{\prime }\leftarrow w_i+\alpha (y-\hat{y})x_i$$

相似的，bias 用以下方式来更新：
$$b^{\prime }\leftarrow b+\alpha (y-\hat{y})$$

需要注意的是，我们计算的是误差的均值，因此添加量应该是 $\frac{1}{m}\cdot \alpha$ 而不是 $\alpha$，这个可以在设置 learning rate 的时候，直接设置成 $\frac{1}{m}\cdot \alpha$，但一般还是被称为 $\alpha$。

6.3 Code

因此，每一个权重的更新是这样的：$\Delta w_i=\alpha \ast \delta \ast x_i$，其中 $\alpha$ 是学习率， $\delta$ 是误差项。

误差项由以下公式表示：
$$\delta =(y-\hat{y})f^{\prime }(h)=(y-\hat{y})f^{\prime }\left(\sum w_i{x}_i\right)$$

其中 $f^{\prime }(h)$ 是激活函数 $f(h)$ 的导数，$h$ 为权重乘输入的输出。就像之前提到的，${\sigma }^{\prime }=\sigma (1-\sigma )$

import numpy as np

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1/(1+np.exp(-x))

learnrate = 0.5
x = np.array([1, 2])
y = np.array(0.5)

# Initial weights
w = np.array([0.5, -0.5])

# Calculate one gradient descent step for each weight
nn_output = sigmoid(np.dot(x, w))

error = y - nn_output

del_w = learnrate * error * nn_output * (1 - nn_output) * x

print('Neural Network output:')
print(nn_output)
print('Amount of Error:')
print(error)
print('Change in Weights:')
print(del_w)

7. 神经网络

单层的线性回归满足不了分类需求，因此引出了多层的神经网络作为替代。神经网络具有某些特殊的层级结构：第一层称为输入层，它包括了输入数据，在下方的例子中的输入就是 $x_1$ 和 $x_2$；第二层称为隐藏层，也就是针对输入层的一系列线性模型；最后一层是输出层，多个线性模型组合成一个非线性模型。

如果有多个隐藏层，就形成了深度神经网络：这些线性模型相结合，形成非线性模型，这些非线性模型进一步再结合，形成更多的非线性模型。通常我们可以这么操作很多次，形成具有大量隐藏层的复杂模型。

7.1 多分类问题

对于两个类别的分类问题神经网络的分类效果非常好。但是如果有更多类别呢？

例如我们想要模型告诉我们图片中的动物，是鸭子，海狸，还是海象。我们可以创建一个神经网络来判断图片是否是鸭子，然后创建另一个神经网络来判断是否是海狸，再创建第三个神经网络来判断是否是海象，然后选择概率最大的答案：

但这样似乎太麻烦了，或许只需要最后一个层级告诉我们图片中是哪个动物，我们要做的是在输出层添加更多节点，每个节点都将告诉我们图片属于每种动物的概率，我们得到得分 (score) 并使用之前定义的 SoftMax 函数，得到所需的每种类别的概率，这就是神经网络进行多类别分类的方法。

7.2 链式法则

链式法则的内容是：如果有一个变量 $x$ 以及一个关于 $x$ 的函数 $f(x)$ 我们将简称为 $A$，然后有另一个函数 $g$。将 $f(x)$ 作为 $g$ 的变量得到 $g\circ f(x)$，我们称之为 B。链式法则证明：对复合函数求导，就是一系列导数的乘积。

7.2 神经网络公式

• Feedforward
  
• Backpropagation