一、概率密度函数和分布函数
分布函数是概率密度函数从负无穷到正无穷上的积分;
在坐标轴上,概率密度函数的函数值y表示落在x点上的概率为y;
分布函数的函数值y则表示x落在区间(-∞,+∞)上的概率。
二、均匀分布的概率密度函数
假设x服从[a,b]上的均匀分布,则x的概率密度函数如下


概率密度图像如上图所示
三、均匀分布的分布函数
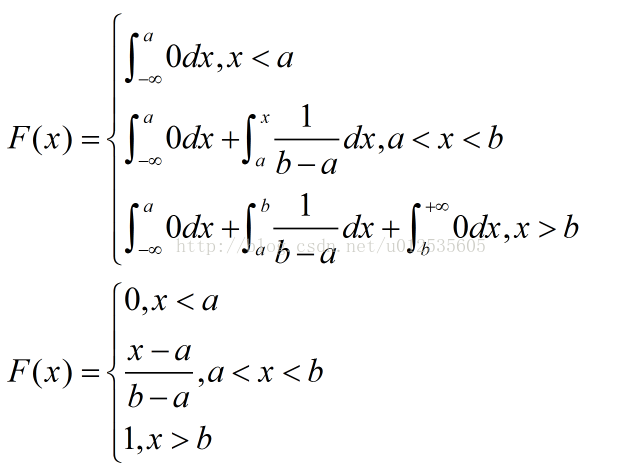

四、均匀分布的期望与方差

一、概率密度函数和分布函数
分布函数是概率密度函数从负无穷到正无穷上的积分;
在坐标轴上,概率密度函数的函数值y表示落在x点上的概率为y;
分布函数的函数值y则表示x落在区间(-∞,+∞)上的概率。
二、均匀分布的概率密度函数
假设x服从[a,b]上的均匀分布,则x的概率密度函数如下


概率密度图像如上图所示
三、均匀分布的分布函数
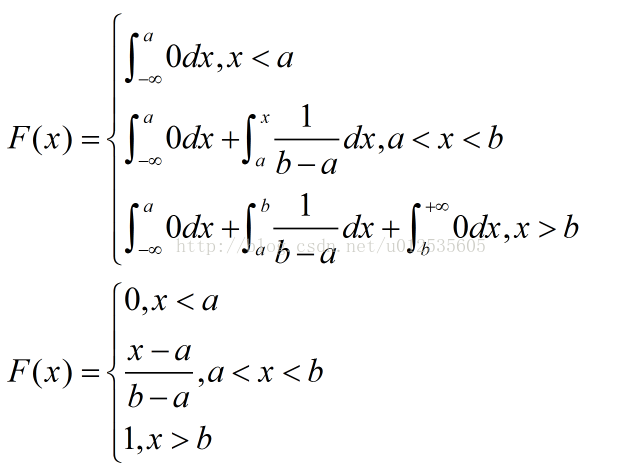

四、均匀分布的期望与方差

 891
891

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


