瞪羚优化算法：一种新型自然启发式优化算法

---

1.摘要

瞪羚优化算法（GOA）是一种新型的基于种群的元启发式算法，灵感来源于瞪羚在以捕食者为主的环境中的生存策略。该算法通过模拟瞪羚逃离捕食者的行为，解决复杂的优化问题。GOA包含两个主要阶段：开发阶段和探索阶段。在开发阶段，模拟瞪羚在安全环境中觅食的行为；在探索阶段，则模拟瞪羚发现捕食者后的逃跑和躲避行为。

2.算法原理

开发阶段

假设瞪羚在没有捕食者或捕食者潜伏的情况下安静地觅食，GOA模拟瞪羚通过均匀和受控的步伐在优化领域的邻域区域进行搜索:
$$\begin{array}{c}{\mathrm{gazelle}}_{i+1}={\mathrm{gazelle}}_i+s.R\ast .R_B\ast .({\mathrm{Elite}}_i-R_B\ast .{\mathrm{gazelle}}_i)\end{array}$$
其中，s表示瞪羚的觅食速度，RB表示布朗运动包含随机数矢量，R为[0,1]随机数。

探索阶段

瞪羚在发现捕食者后立即奔跑，根据迭代次数的奇偶性，瞪羚的移动方向会相应改变。研究中假定瞪羚首先使用Levy飞行进行反应，而捕食者则先使用布朗运动开始追逐，随后转为Levy飞行：
$$\begin{array}{rl}\overrightarrow{{\mathrm{gazelle}}_{i+1}}& =\overrightarrow{{\text{gazelle}}_i}+S.\mu .\vec{R}\ast .{\vec{R}}_L\\ & \ast .\left(\overrightarrow{{\mathrm{Elite}}_i}-\overrightarrow{R_L}\ast .\overrightarrow{{\mathrm{gazelle}}_i}\right)\end{array}$$
其中，S为瞪羚最高速度，捕食者追逐瞪羚行为：
$$\begin{array}{rl}\overrightarrow{{\mathrm{gazelle}}_{i+1}}& =\overrightarrow{{\mathrm{gazelle}}_i}+S\cdot \mu \cdot \mathrm{CF}\ast \cdot {\vec{R}}_B\\ & \ast \cdot \left(\overrightarrow{{\mathrm{Elite}}_i}-\overrightarrow{R_L}\ast \cdot \overrightarrow{{\mathrm{gazelle}}_i}\right)\end{array}$$

PSRs是捕食者成功率，这一效应影响瞪羚的逃逸能力：
$$\begin{array}{rl}& \overrightarrow{{\mathrm{gazelle}}_{i+1}}\\ & =\{\begin{array}{ll}\overrightarrow{{\mathrm{gazelle}}_i}+\mathrm{CF}[\overrightarrow{\mathrm{LB}}+\vec{R}\ast .(\overrightarrow{\mathrm{UB}}-\overrightarrow{\mathrm{LB}}\left)\right]\ast \cdot \vec{U}& \text{if}r\le \text{PSRs}\\ \overrightarrow{{\mathrm{gazelle}}_i}+[\mathrm{PSRs}(1-r)+r](\overrightarrow{{\mathrm{gazell}}_{r_1}}-\overrightarrow{{\mathrm{gazelle}}_{r_2}})& \text{else}\end{array}\end{array}$$

流程图

伪代码

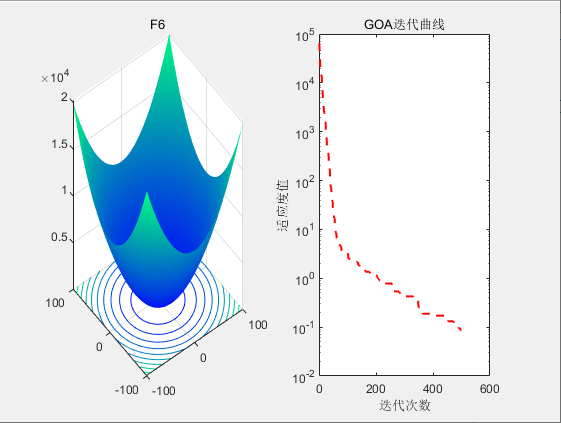
3.结果展示

4.参考文献

[1] Agushaka J O, Ezugwu A E, Abualigah L. Gazelle optimization algorithm: a novel nature-inspired metaheuristic optimizer[J]. Neural Computing and Applications, 2023, 35(5): 4099-4131.

5.代码获取