[统计学] 对如何设计抽样模型的思考

  

一、说明

   在本章中，我们将探讨进行假设检验时需要了解的 3 个重要分布：总体分布、样本分布和抽样分布。最重要的是，我们将探索它们之间的关系，以便您不仅内化它们是什么，而且内化它们为什么重要。

二、什么是人口分布？

   总体当然是您有兴趣研究的整个个体群体。这可以是从所有人到特定类型细胞的任何事物。然而，人口分布的定义有点窄，因为它特定于您感兴趣的度量。因此，如果您研究成年人的身高，您的人口将全部是成年人，但您的人口分布将全部是成年人每个人的身高以厘米为单位。许多资源并没有做出这种严格的区分，但如果您以这种方式考虑人口分布，它将帮助您准确地概念化您的人口参数是什么。

2.1 什么是总体参数？

   总体参数是描述总体分布的数字。在大多数现实世界的实验设置中，如果您的数据是连续的，您可能对总体均值最感兴趣。如果您有分类数据，您可能会对适用某种特征的人口比例感兴趣。您最终可能会得到应用不同参数的二进制或计数数据。但实际上，研究人员通常对平均值感兴趣，如果您了解以下有关总体的原则，则意味着很容易将这些知识转移到您感兴趣的任何其他总体参数。请注意，尽管我们对人口平均值，这并不意味着我们假设人口分布的任何形状（即无论分布是什么形状，您都可以计算平均值）。我们将在以后的章节中进一步讨论假设检验的假设。

   在频率统计中（即我们在贝叶斯统计之前要讨论的所有内容）总体参数是固定值。这具有直观意义，例如，所有人类都有一个真正的平均身高。当然，实际访问这些总体参数是不寻常的。一个值得注意的例外是，当您使用标准化测试数据（例如 IQ 分数）时，测试平均值被设计为特定值。然而，当您观察自然界中的某些事物时，您将无法访问总体值（如果您这样做了，您就不需要统计数据）。

2.2 什么是样本分布？

   因为我们不知道总体参数，所以我们必须使用样本来估计它们。您的样本是您实际观察到的唯一数据，而其他分布更像是理论概念。因此，您的样本分布是您尝试研究的总体分布的观察值。我们处理的不是描述总体的理论常数参数，而是总结样本的统计数据。这可能会令人困惑，因为总体平均值是参数，但样本平均值是统计量。为了帮助澄清问题，有不同的数学符号来描述参数和统计数据。常见参数有平均值 μ、标准差 σ 或 p 比例。统计等效值是平均值$\bar{x}$ （读：“x bar”）、标准差 s 和比例$\hat{p}$ （读：“p hat”）。虽然这些符号很常见，但检查上下文以区分是否引用母体参数或统计数据总是有益的。
   在某些领域，如何收集样本非常重要。例如，在对政治信仰进行民意调查时，您希望确保您的样本能够代表您所针对的所有人。抽样重要性的一个著名例子来自《文学文摘》，该民意调查对美国富人进行了过度抽样，结果预测兰登将在 1936 年赢得美国总统职位。事实上，罗斯福以压倒性优势获胜。在其他领域，预计您会进行简单的随机抽样，而其他抽样方法很少见。
   由于本主题更多的是关于实验设计而不是统计本身，因此我不会在这里讨论不同类型的抽样，但如果您与个体差异较大的人群（例如人）一起工作，我鼓励您阅读更多内容。从现在开始，每当我们讨论样本时，我们都会假设它代表总体。但是，大家要有明确意识：抽样设计是第一重要的前提。

​
   最后，我想快速谈谈异常值。在某些领域，通常的做法是删除与样本均值有一定距离（通常为 2 或 3 sd，或 1.5 IQR）的异常值。

图中表示，IQR为6，当x离中心距离大于1.5IQR时，被认为异常而删除。

   虽然这些方法可以用来识别可能的异常值，但我强烈建议您不要单方面且不加思考地使用这些方法。如果您记录正态分布中的 50 个数据点，您应该预计在大约 12.5% 的时间内观察到至少一个“异常值”（如果任何点距均值大于 3 标准差，则为异常值）。在我看来，删除异常值的唯一原因是您认为该异常值不是由您的人口分布产生的。
   需要查清异常产生原因，例如，如果你让受试者完成一项心理任务，但其中一个受试者在整个过程中睡觉，导致表现不佳，那么将他们从你的分析中删除当然是有意义的。
   但是，如果您的任务的平均表现为 90%，而 1 个受试者的平均表现为 80%，那么在没有其他原因的情况下删除它们可能会使您的结果产生偏差。
   无论如何，每当您考虑删除异常值时，最好在存在和删除异常值的情况下执行分析。然后您可以比较结果，看看该决定是否真的重要。如果没有，请选择对您更有意义的方法，但如果确实重要，请务必报告您的分析受到数据中潜在异常值的严重影响。

三、总体分布与抽样分布之间的关系

   您的样本分布将近似代表您的总体分布。这是合乎逻辑的。如果你的总体是抛硬币的，那么你的样本也必须是二元的。此外，如果您的总体分布正面朝上的概率为 50%，那么您预计样本中大约有 50% 是正面朝上。下面是一个小部件，可让您从总体中生成单个样本。与上一章中的小部件类似，您可以控制生成总体的分布类型。但是，您现在还可以控制使用滑块生成的样本的大小。花点时间探索不同样本大小对样本分布形状的影响。

​
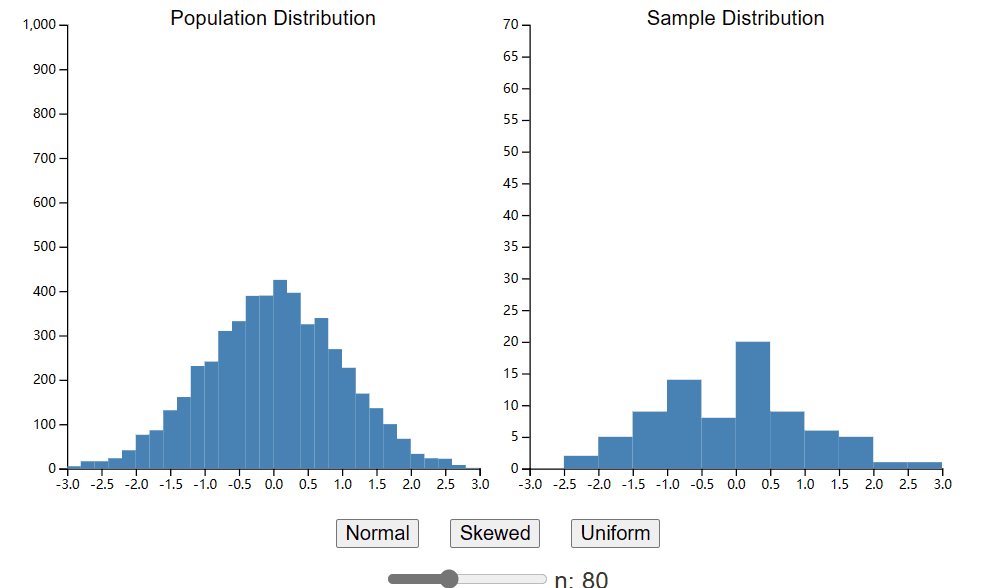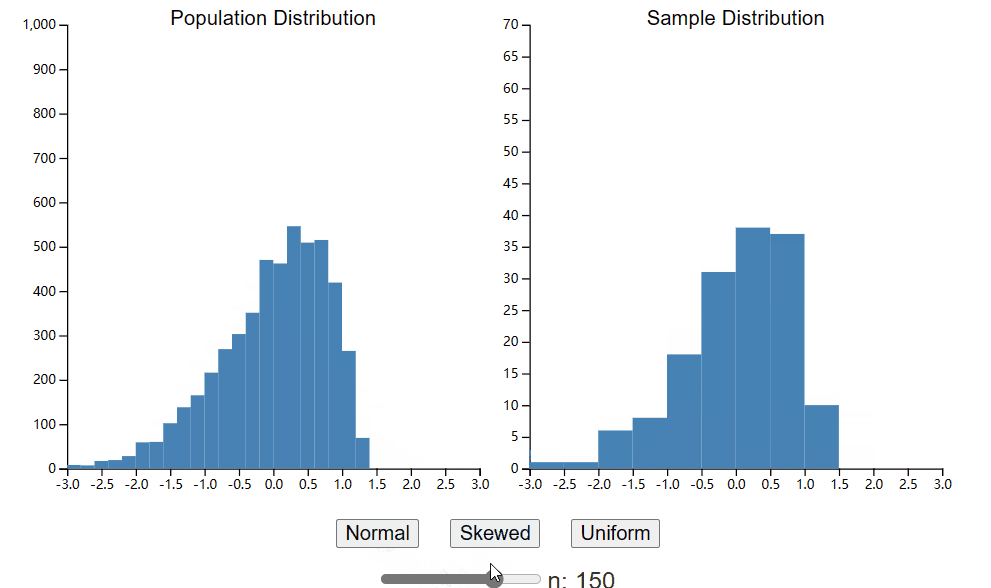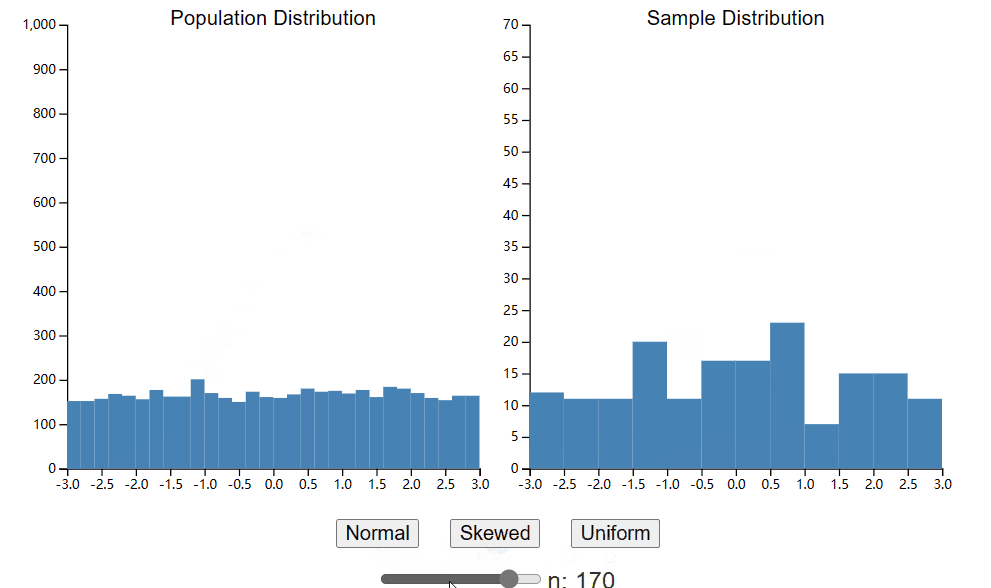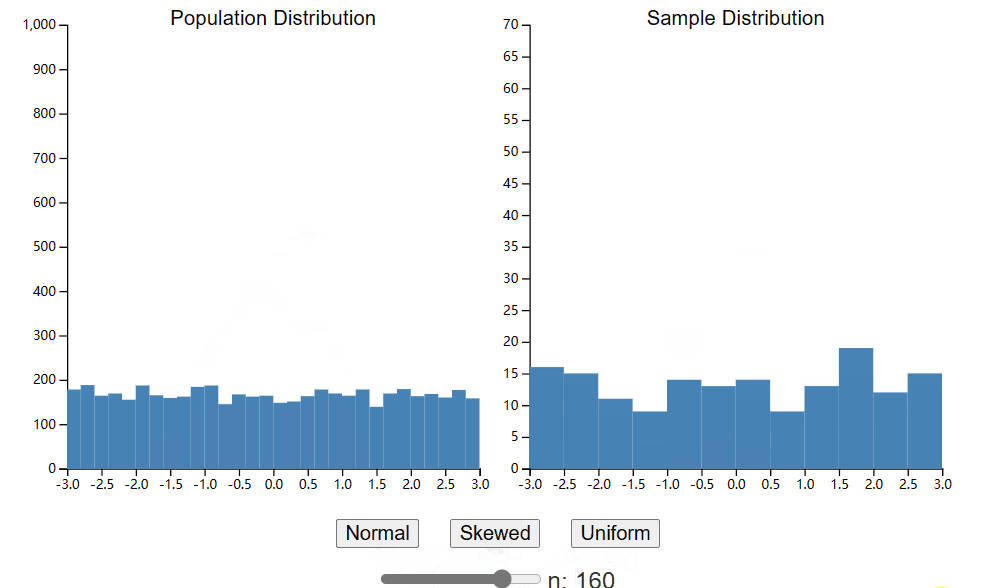
   希望您注意到，随着样本量的增加，样本总体开始看起来更像总体数据。对于大样本量，样本均值和标准差将很好地近似总体均值和标准差。然而，您可能会惊讶于在较小的集合大小下样本分布的表示有多么糟糕。当 n = 20 时，甚至很难区分正态分布和均匀分布，也不可能区分偏斜分布中的偏斜和随机噪声。这并不是说您永远不应该使用 20 个样本进行实验，因为我们将看到即使从小样本中我们也可以学到很多东西。但需要注意的是，如果您的样本量较小，您应该谨慎地对总体分布的形状做出结论。我经常在网上看到研究人员提出的问题，担心他们的数据不正常，而这种规模的样本基本上不可能看起来正常。8在接下来的章节中，我们将研究各种测试的假设以及违反这些假设时会发生什么，以便您知道可以改变哪些规则以及可以改变多远。现在，返回到小部件并确定您愿意根据您收集的样本对人口分布的形状做出声明的样本大小。

​3.1 什么是抽样分布？

   总体和样本分布背后的想法可能对您有一些直观的意义。抽样分布是人们容易遇到麻烦的地方，这是不幸的，因为它们是理解前进的最重要的（当然，命名没有帮助）。抽样分布是样本统计量可能值的理论分布。让我们回到抛硬币的例子。正如我们之前所看到的，有可能但不太可能观察到具有 10/10 头的样本，而观察到具有 5/10 头的样本的可能性则更大。这就是我们的抽样分布所包含的信息。

   为什么抽样分布的概念如此重要？在频率统计中，我们估计中有关不确定性的所有信息都来自我们了解的有关抽样分布的信息。因为我们的样本来自理论抽样分布，所以我们可以向后推算关于抽样分布的声明。而且，通过从我们的抽样分布中逆推，我们可以对总体参数估计的不确定性做出断言。

​

3.2 抽样分布与总体分布之间的关系

   在统计中，大多数时候我们处理的是单个样本。9如果没有上一章讨论的概率定理，我们将无法对抽样分布做出任何陈述。幸运的是，由于中心极限定理，我们知道平均值的抽样分布将是正态的。由于大数定律，我们知道随着 n 的增加，总体平均值的变异将会减小。

   下面的小部件将允许您探索人口分布的变化如何影响抽样分布。抽样分布显示样本均值的分布，其中每个样本的 n 为 25。此小部件与 CLT 小部件相同，但您现在可以调整总体分布的均值和标准差。花点时间看看这些变化如何影响抽样分布。

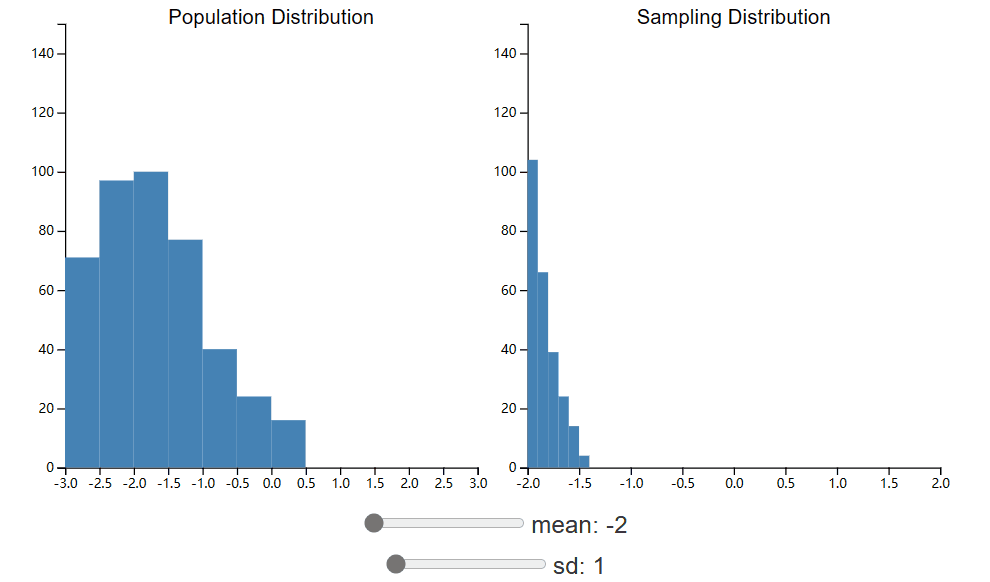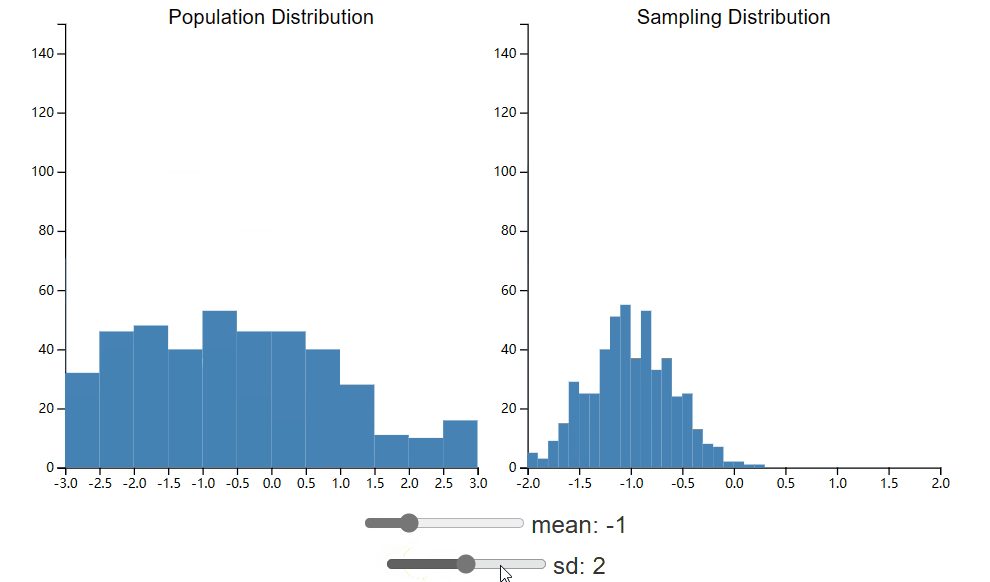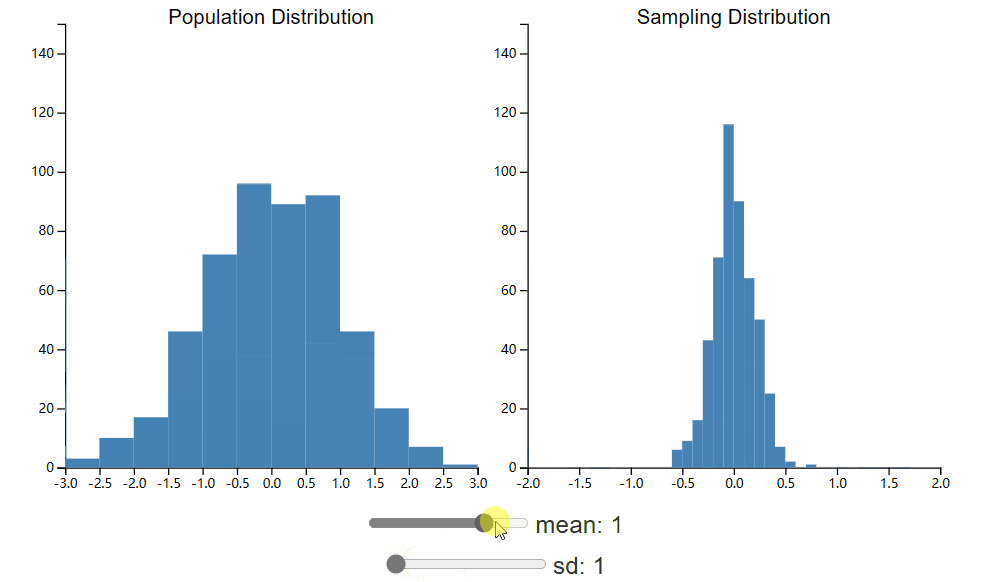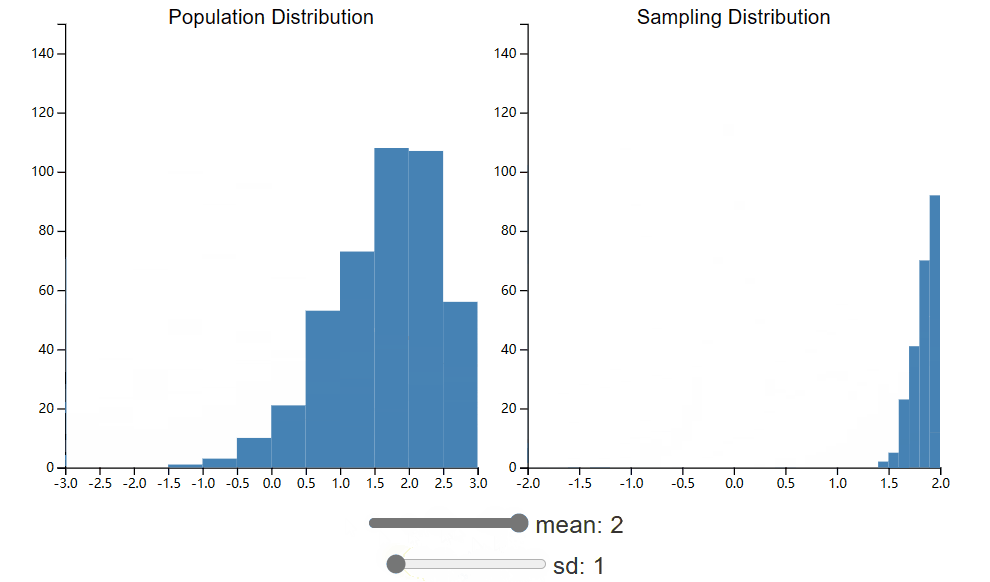
   正如您希望注意到的那样，改变总体分布的均值会导致抽样分布中心的变化。这是什么意思？这意味着样本均值更有可能接近总体均值，而不是远离总体均值。感谢 CLT，我们知道总体均值周围的误差将呈正态分布。然而，抽样分布的标准差并不是总体 σ 的估计。尽管如此，其中仍然存在着明显的关系，我们将在以下各节中继续探讨这一关系。

3.3 抽样分布与样本分布的关系

   在这里，我们将进一步探讨样本量对样本分布的影响。在下面的小部件中，并排绘制了总体样本和抽样分布。您可以再次控制总体标准差（这直接影响样本标准差），但现在您还可以更改已收集的样本大小。比较调整这两个值时采样分布的形状如何变化。

​
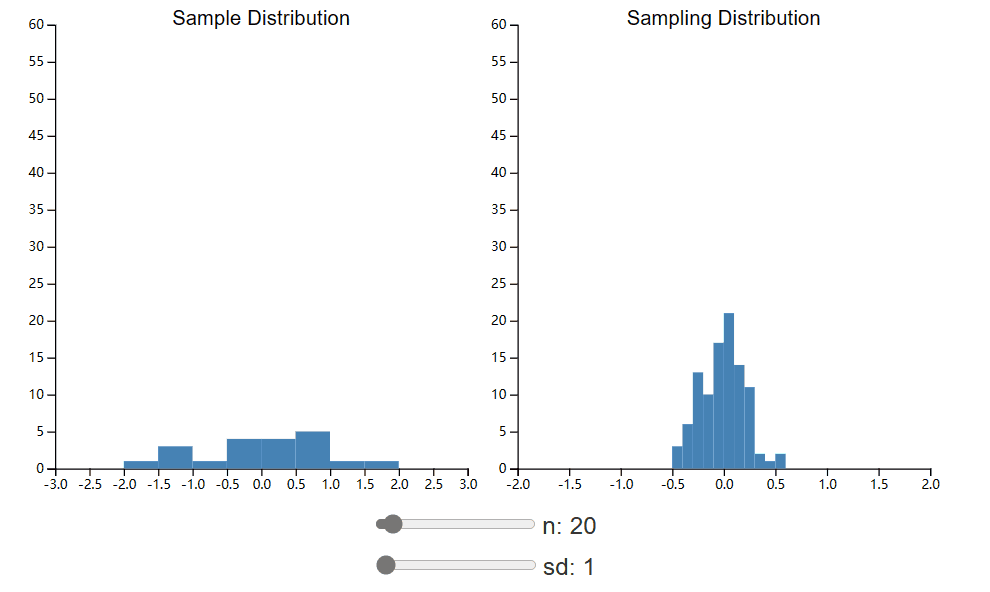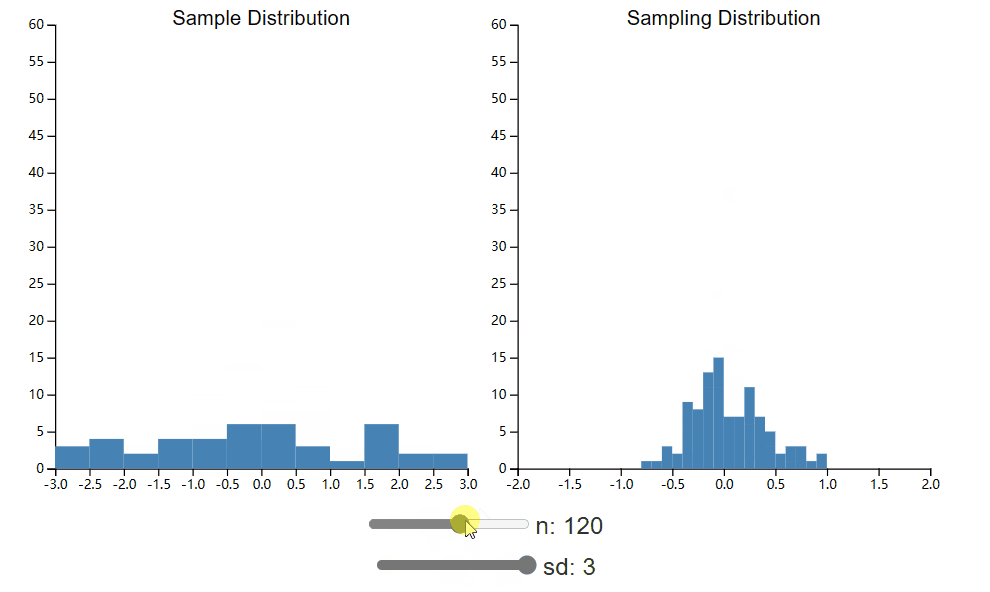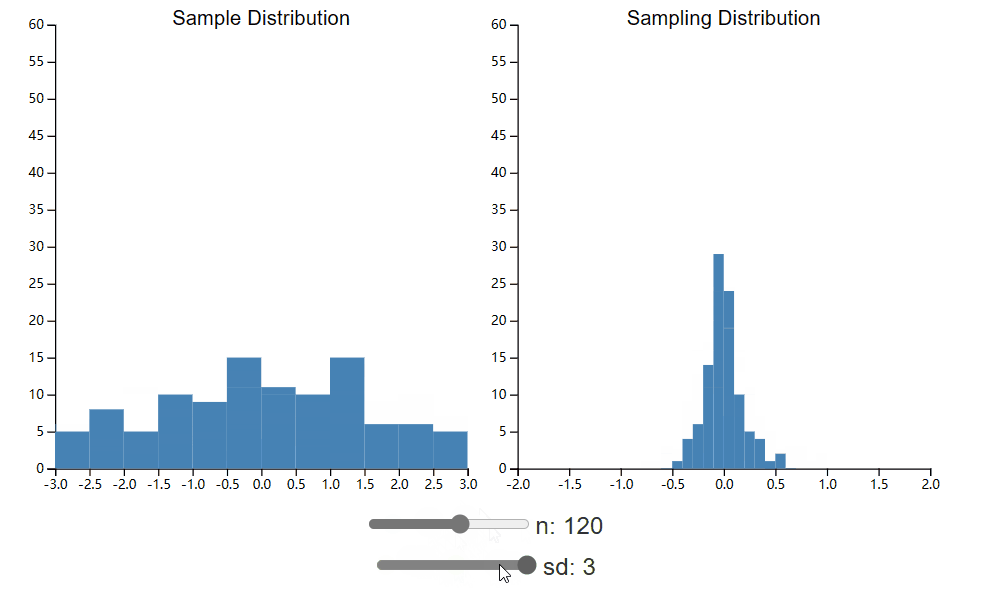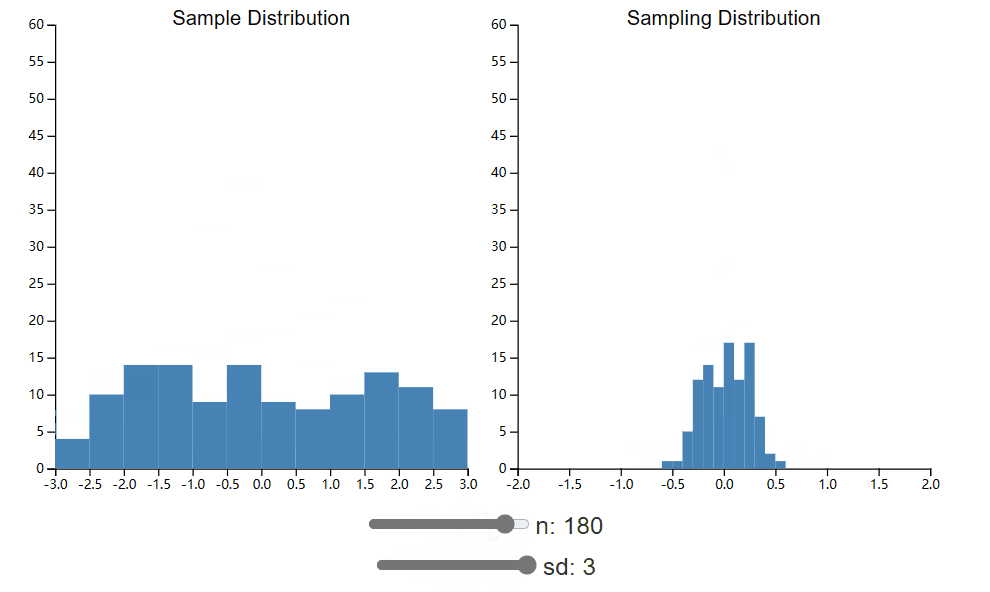
   首先，请注意，即使集合大小很小，我们最终也会得到看起来正常的采样分布。有一个经常重复的“规则”，即中心极限定理在 n = 30（或者最近甚至是 50）时生效，并且如果没有这么大的样本量，假设检验就无效。正如您所看到的，当我们的总体呈正态分布时，这条规则并不适用，即使 n 为 10 也足以满足良好的正态抽样分布。如果您要使用二项式分布重复此过程，您可能会发现，即使 n 为 50，也比您预期的更偏离正态分布。10不要盲目相信经验法则。相反，请花时间为自己、针对您的特定情况进行这些模拟。

   希望您还看到较小的 sd 值和较大的 n 值都会导致更窄的采样分布。这有什么意义呢？请记住，这是我们观察到的样本均值的均值分布。更细的分布意味着我们的样本均值可能比其他情况更接近总体均值。换句话说，我们的估计变量越小，样本越多，我们对总体参数的估计就越好。返回小部件并回答以下问题。假设您有资源来减少样本噪声（导致样本标准差更小）或增加样本数量，您应该选择哪一个？这对抽样分布标准差的数学定义有何直观意义？

​

四、标准误

   抽样分布的标准偏差称为标准误差 (SE)。标准误差有多个公式，具体取决于您的抽样分布是什么，但在这里我们将讨论上面显示的标准误差背后的数学原理。简单均值估计的标准误差是总体 sd 除以样本大小 n (3.1)的平方根。
$SE=\frac{\sigma }{\sqrt{n}}$ (3.1)

   然而，由于我们通常无法获得总体参数 sigma，因此我们使用样本标准差，因为它是总体标准差的估计。对于极小的样本（即小于 5），此估计存在偏差，但随着 n 的增加，它在很大程度上可以忽略不计。

   该公式的结果之一是，如果可以选择的话，通常减少噪声比增加样本量更好。随着样本量的增加，由于分母的平方根，回报会递减。在心理学实验中，这意味着让 50 名受试者完成 50 次实验试验可能比 100 名受试者完成 25 次试验更好。11

   如果您有兴趣，我鼓励您研究抽样分布的均值和标准差的推导。它们非常简单，有助于巩固包含独立同分布 (iid) 随机变量的样本的重要性。然而，如果您从本节中学到的只是完全理解标准错误的定义，那么您仍然会处于一个良好的前进位置。

五、一些思考

1 您可以简单地计算您感兴趣的任何样本大小。单个数据点为异常值（距平均值大于 3 sd）的概率约为 0.0027（考虑如何使用正态 cdf 来计算此值）。整个样本中没有异常值的几率为 (1 - 0.0027)^n，其中 n 是样本大小。最后，要获得至少一个异常值的几率，只需用 1 减去该值即可。例如，50 个样本中至少有一个异常值的几率为 1 - ((1 - 0.0027)^50)。

你也可以用类似mean(replicate(100000, {x = rnorm(50); any(x > 3 | x < -3)}))

2 ​至少在直方图中是这样。 QQ 图可以更好地显示与正态性的真实偏差。
3 即使数据来自多个不同的地方，您通常仍会将其视为单个样本并包含一个因素或使用集群来解释差异。

4 在 R 中使用 自行检查x = rbinom(1000, 50, 0.5); qqnorm(x); qqline(x)

5 具体细节取决于 sd 如何随着您所包含的试验数量而变化，因此如果有可用的大型数据集，则值得进行一些下采样分析。3让我们探索一下抽样分布
​

​