本文介绍了大数定律的基本概念，探讨了样本容量与误差的关系，以及弱大数定律和强大数定律在统计学中的作用。通过实例说明，随着样本量增大，样本均值更准确地反映总体均值，且在独立实验中，样本比例趋向于真实比例。中心极限定理与大数定律相辅相成，共同构建了抽样理论的基础。
一、说明
大数定律和中心极限定律无疑是抽样理论最重要的理论支持。注意这两个定律是以公理形式出现，因此不要试图证明。有种种案例可以强化对这两个公理的理解。本篇将叙述大数定律的意义，合理性，约束条件。从直观上加强对这个理论的理解。
二、大数定律观念
2.1 样本容量和误差关系
大数定律简单地表明，随着样本量的增加，样本均值准确表示真实总体均值的概率也会增加。这是表示样本越大越准确的正式数学方法。
大数定律与中心极限定理有关，特别是方差和标准误差的公式。请注意，样本大小出现在这些公式的分母中。任何分数中的分母越大，意味着该分数的总值越小（即 1/2 = 0.50、1/3 – 0.33、1/4 = 0.25 等）。
因此，较大的样本量将产生较小的标准误差。我们已经知道标准误差是抽样分布的分布，较小的分布会产生较窄的分布。因此，较大的样本量会产生较窄的抽样分布，这会增加样本均值接近中心的概率，并降低样本均值位于尾部的概率。这在图中进行了说明：
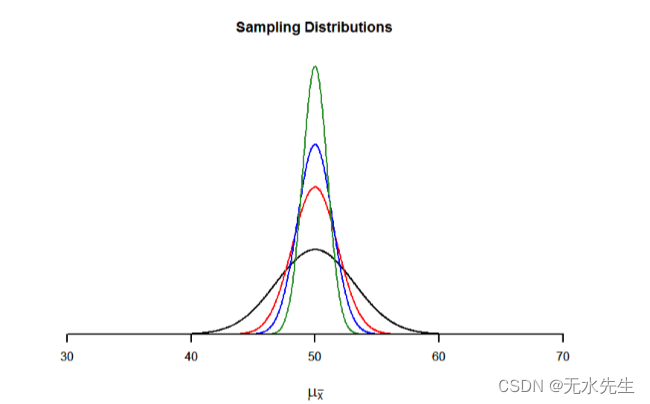
图3.2 ：从同一总体中抽样分布μ= 50 和σ= 10 但样本量不同（N= 10,N= 30,N= 50,N= 100）
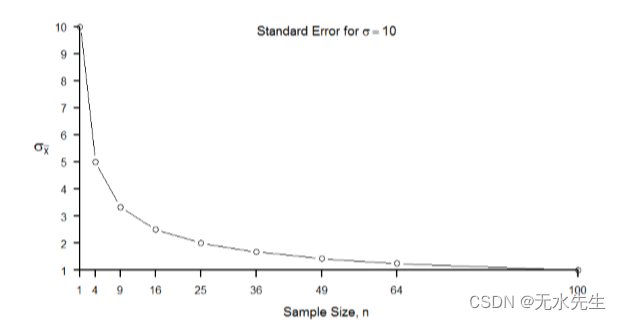
数字3. 3：样本量与常数标准误差之间的关系σ= 10
本页标题为6.2：样本均值的抽样分布，在CC BY-NC-SA 4.0许可下共享，由Foster 等人 创作、重新混合和/或策划。 （密苏里大学的负担得起的开放教育资源计划）通过根据 LibreTexts 平台的风格和标准编辑的源内容；可根据要求提供详细的编辑历史记录。
2.2 高斯母体的大数定律
假设我们独立地一遍又一遍地进行相同的实验。并假设我们对一个事件发生的相对频率感兴趣，该事件在每次实验中观察到的概率为p。然后，随着（相同且独立）实验数量的增加，该事件的观察到的样本频率与重复总数的比率向p收敛。这是 LLN 的非正式声明。
考虑另一个例子，我们研究一个 100 名学生的班级的平均身高。与该班随机抽取的 3 名学生的平均身高相比，随机抽取的 10 名学生的平均身高很可能更接近所有 100 名学生的真实平均身高。这是事实，因为 10 个样本比只有 3 个样本的样本数量更大，并且可以更好地代表整个班级。在一种极端情况下，从 100 名学生中抽取 99 名作为样本，得出的样本平均身高几乎与所有 100 名学生的平均身高完全相同。在另一个极端，对单个学生进行抽样将是对整个班级平均身高的极其不同的估计。
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3095954/
三、大数定律
大数定律分弱大数定律和强大数定律，针对不同的问题，可以选择不同的大数定律给以解释。
上图中，左图是弱大数定律，右图是强大数定律。
针对各种各样的抽样设计，有的满足弱大数定律，有的满足强大数定律，在实际应用中可以选择性使用。
3.1 弱大数定律
LLN 的两个最常用的符号版本包括弱大数定律和强大数定律。
弱大数定律的表述意味着，随着样本量的增加，随机样本的平均值以概率收敛于期望值。表述为，
X
ˉ
n
→
p
μ
此时
n
→
∞
\bar{X}_n\overset{p}{\rightarrow} \mu 此时 n\rightarrow \infty
Xˉn→pμ此时n→∞
对于给定的 ε > 0，这种概率收敛的定义为
lim
x
→
∞
P
(
∣
X
n
−
μ
∣
<
ε
)
=
1.
\lim_{x\to\infty}P( ∣X_n−μ∣<ε)=1.
x→∞limP(∣Xn−μ∣<ε)=1.
本质上，弱 LLN 表示，只要我们可以增加样本量，许多观测值的平均值最终将在总体平均值的任何误差范围内。
3.2 强大数定律
顾名思义，强大数定律意味着弱 LLN，因为它依赖于样本平均值几乎肯定（a.s.）收敛于总体平均值。象征性地，
X
ˉ
n
→
a
.
s
μ
此时
n
→
∞
.
,
i
.
e
.
,
P
(
lim
n
→
∞
X
ˉ
n
=
μ
)
=
1.
\bar{X}_n \overset{a.s}{→} \mu 此时 n →∞.,i.e.,P(\lim_{n→∞} \bar{X}_n= \mu)=1.
Xˉn→a.sμ此时n→∞.,i.e.,P(n→∞limXˉn=μ)=1.
强 LLN 解释了总体平均值（或期望值）与独立观测值的样本平均值之间的联系。
通常有必要将正式的 LLN 陈述（就样本平均值和收敛类型而言）与 LLN 的常见解释（就各种事件的概率而言）进行比较。 （强）LLN 意味着样本比例几乎肯定会收敛到真实比例。根据 SOCR LLN 小程序，对这种收敛的一种实际解释如下：如果我们重复小程序模拟固定的次数（尽管次数很大），那么我们几乎肯定会观察到一个似乎不收敛的序列。然而，几乎所有序列都会出现收敛——并且在运行小程序模拟时通常会观察到这种行为。当然，当以连续模式运行小程序时，观察到非收敛行为的概率是微不足道的，并且样本大小没有限制。
3.3 强大数定律的一个示例
假设我们多次独立观察同一过程。假设每个试验结果的二值化（二分）函数是有意义的。例如，失败可能表示连续电压测量值 < 0.5V 的事件，而补充，成功则表示电压≥ 0.5V。电子芯片就是这种情况，通过将电流二值化为 0 或 1 来执行算术运算。研究人员通常对观察给定试验的成功事件或由多次试验组成的实验中成功的次数感兴趣。让我们在每次试验中表示 p=P(成功)。那么，样本中成功的总数与试验次数（n）的比值就是平均值.
代表第 i 次试验的结果。因此，样本平均值等于样本比例
(
X
n
=
p
^
)
(X_n=\hat{p} )
(Xn=p^)。样本比例（该事件的观察频率与重复总数的比率）估计真实的 p=P(success)。因此，随着（相同且独立）试验数量的增加，
p
^
\hat{p}
p^向 p 收敛。
四、结论
大数定律和中心极限定律是一个问题的两个方面，中心极限定律解决的是方向性问题，告诉你样本的均值（或其它参量）极限存在。大数定律告诉你，如何去逼近极限，即N趋近无穷大后，中心极限得以实现。
https://open.maricopa.edu/psy230mm/chapter/chapter-8-sampling-distributions/
https://www.investopedia.com/terms/l/lawoflargenumbers.asp
https://www.probabilitycourse.com/chapter7/7_1_1_law_of_large_numbers.php
https://www.scribbr.com/statistics/central-limit-theorem/
扫一扫
2887
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
