生活中的数学（为生活建模）（二）

本文链接：https://blog.csdn.net/lanchunhui/article/details/50570015

本文探讨了日常生活中的数学原理，包括0/1背包问题的概率模型、等差数列求和的快速计算方法、黄金分割比的概念及其应用，以及经典的鸡兔同笼问题。通过这些实例，展示了数学在解决实际问题中的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

生活中的数学（为生活建模）
生活中的数学（为生活建模）（二）
生活中的数学（为生活建模）（三）

样本空间大小的计算

所谓等式，即是对一个问题的不同描述；

(n 0) + (n 1) + \dots + (n n) = (1 + 1) n = 2 n

$\binom n0+\binom n1+\cdots+\binom nn=(1+1)^n=2^n$

0/1背包问题，也即 $n$ 中商品有取或者不取两种状态，其样本空间大小为， $2^n$ ，自然也就等以 $\binom n0+\binom n1+\cdots+\binom nn$

$1+2+\cdots+100$

数学王子高斯上小学三年级的时候就以一种极快的方法给出了： $1+2+\cdots+100$ 的结果以及计算方法，也即：

1 + 2 + 3 + \dots + 98 + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + \dots + (50 + 51) = 101 \times 50 = 5050

$\begin{array}{l} 1+2+3+\cdots+98+99+100&=(1+100)+(2+99)+(3+98)+\cdots+(50+51)\\ &=101\times 50=5050 \end{array}$
再稍作泛化就是等差数列的前

n $n$ 项和公式：

S n = ( a 1 + a n ) n 2

$S_n=\frac{(a_1+a_n)n}2$
高斯的解法是稍微有一些问题（不是说错），如果当时老师问的是1加到99，可能还需解决一些问题。所以一种更为 tricky 的方式，也是等差数列前

n $n$ 项和的求和公式：

S n = 1 + 2 + \dots + 99 + 100 S' n = 100 + 99 + \dots + 2 + 1 1 + 2 + \dots + 99 + 100 = S n + S ' n 2 = 101 \times 100 2

$\begin{array}{l} S_n =1+2+\cdots+99+100\\ S'_n=100+99+\cdots+2+1\\ 1+2+\cdots+99+100=\frac{S_n+S_n'}2=\frac{101\times 100}2 \end{array}$

黄金分割比

a a + b = b a a 2 - a b - b 2 = 0 ⇓ x = b a x 2 + x - 1 = 0 ⇓ x = 5 \sqrt - 1 2

$\frac a{a+b}=\frac ba\\ a^2-ab-b^2=0\\ \Downarrow {x=\frac ba}\\ x^2+x-1=0\\ \Downarrow\\ x=\frac{\sqrt 5-1}2$
也即

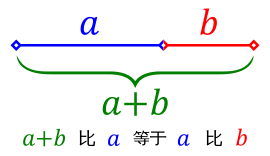
ba=5√−12 $\frac ba=\frac{\sqrt 5-1}2$ ，自然

ab=5√+12 $\frac ab=\frac{\sqrt 5+1}2$

鸡兔同笼问题

我们首先给出其数学（初等代数）形式，通常意义下的求解与解释如下：

x + y = 15 2 x + 4 y = 40 (1) (2)

$\begin{split} \begin{array}{lr} x+y=15&(1)\\ 2x+4y=40&\qquad\qquad(2) \end{array} \end{split}$

然后 $(2)-2\times (1)$ ，首先解得 $y$ ，最后求解 $x$ 。我们首先分析 $(2)-2\times (1)$ 可能代表的物理（现实）意义。后来我在微信公众号看到了一种有趣的解释，说让鸡与兔同时抬起一只脚，鸡与兔再同时抬起一只脚，剩下的10只脚，每只兔子还剩2只脚，则有五只兔子。