开根号

一个数能够开根号的前提是，其全部因子，必须成对出现（偶数次），而不可以是奇数次。

• 一个偶数如果能够开根号（是偶数，则存在 2 的因子，因为能够开根，则其因子需成对出现），则其开根号的结果一定也是偶数；
• 一个奇数如果能够开根号（不存在 2 ），则其开根号的结果一定也是奇数；

1. $y=x^2$ 与 $y=\sqrt x$

首先二者互为反函数，又因为 $\sqrt x$ 的定义域限制，可得 $y=x^2$ 与 $y=\sqrt x$ 在第一象限关于 $y=x$ 对称。

• $\sqrt x\geq x$ ⇒ $0 \leq x \leq 1$
• $1<a<2$，对其无论开多少次根号，$a^{\frac1{2^k}}$ 其值都会大于 1，而不会小于 1；

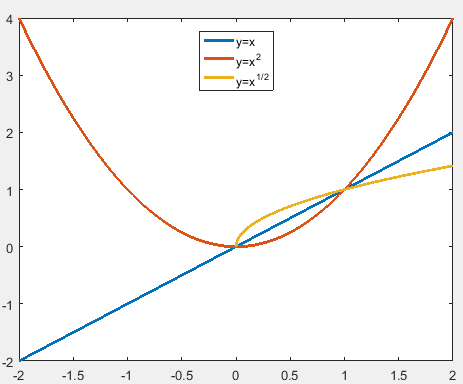
$y=x$, $y=x^2$, $y=\sqrt x$，三条线的关系如下图所示：