四元数的球面线性插值(slerp)

Reference:

1. 四元数插值与均值（姿态平滑）
2. MathWorks:slerp
3. 四元数的球面线性插值（slerp）
4. Quaternion kinematics for the error-state KF

1. 概念

对于一般线性插值来说：$\mathbf{r}={\mathbf{P}}_0+\left({\mathbf{P}}_1-{\mathbf{P}}_0\right)t$，其中 $\mathrm{t}\in [0,1]$，代表了插值矢量 $\mathbf{r}$ 末端在弦 ${\mathbf{P}}_0-{\mathbf{P}}_1$ 上的位置。假如 $t$ 取值为 $1/4$、$2/4$、$3/4$ 即将 ${\mathbf{P}}_0{\mathbf{P}}_1$ 弦长均分为 $4$ 等份, 可以看出其对应的弧长并不相等。靠近中间位置的弧长较长，而靠近两段处的弧长较短，这就意味着当 $t$ 匀速变化时，代表姿态矢量的角速度变化并不均匀：

球面线性插值(Spherical linear interpolation, 通常简称Slerp)是四元数的一种线性插值运算，主要用于在两个表示旋转的四元数之间平滑差值。

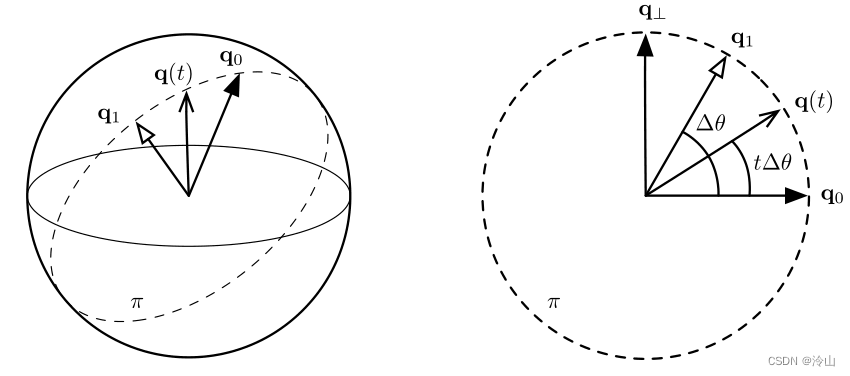
通常Slerp会用在SLAM轨迹插值中，设 $\mathbf{p}$ 对应的时刻为 $t_1$，$\mathbf{q}$ 对应的时刻为 $t_2$，$t^{\prime }$ 时刻对应的四元数为 $\mathbf{r}$，即为所求，于是比例系数 $t$ 满足：
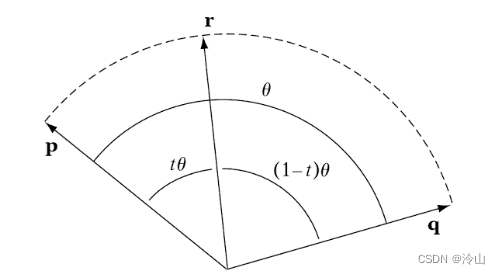
$$t=\frac{t^{\prime }-t_1}{t_2-t_1}$$注意单位四元数 $\mathbf{p}$ 和 $\mathbf{q}$ 之间的夹角为 $\theta$，$\mathbf{p}$ 和 $\mathbf{r}$ 之间的夹角为 $t\theta$，$\mathbf{q}$ 和 $\mathbf{r}$ 之间的夹角为 $(1-t)\theta$。按一般的插值公式写出 $\mathbf{r}$ 的表达式如下，即要找到合适的 $a(t)$ 和 $b(t)$：
$$\mathbf{r}=a(t)\mathbf{p}+b(t)\mathbf{q}$$同时有：
$$\cos \theta =\mathbf{p}\cdot \mathbf{q},\cos (t\theta )=\mathbf{p}\cdot \mathbf{r},\cos [(1-t)\theta ]=\mathbf{q}\cdot \mathbf{r}$$用 $\mathbf{p}$ 同时点乘 $\mathbf{r}=a(t)\mathbf{p}+b(t)\mathbf{q}$ 两边可以得到：
$$\begin{array}{l}\mathbf{p}\cdot \mathbf{r}=\mathbf{p}\cdot [a(t)\mathbf{p}+b(t)\mathbf{q}]\\ \cos (t\theta )=a(t)+b(t)\cos (\theta )\end{array}$$用 $\mathbf{q}$ 同时点乘 $\mathbf{r}=a(t)\mathbf{p}+b(t)\mathbf{q}$ 两边可以得到：
$$\begin{array}{c}\mathbf{q}\cdot \mathbf{r}=\mathbf{q}\cdot [a(t)\mathbf{p}+b(t)\mathbf{q}]\\ \cos [(1-t)\theta ]=a(t)\cos (\theta )+b(t)\end{array}$$联立上面两个公式可得：
$$\begin{array}{c}a(t)=\frac{\sin [(1-t)\theta ]}{\sin \theta }\\ b(t)=\frac{\sin (t\theta )}{\sin \theta }\end{array}$$于是有：
$$\mathrm{Slerp}(\mathbf{p},\mathbf{q},t)=\frac{\sin [(1-t)\theta ]\cdot \mathbf{p}+\sin (t\theta )\cdot \mathbf{q}}{\sin \theta }$$

也就是MATLAB上写的：

• Quaternion spherical linear interpolation (SLERP) is an extension of linear interpolation along a plane to spherical interpolation in three dimensions. Given two quaternions, $q_1$ and $q_2$, SLERP interpolates a new quaternion, $q_0$, along the great circle that connects $q_1$ and $q_2$. The interpolation coefficient, $T$, determines how close the output quaternion is to either $q_1$ and $q_2$.

  The SLERP algorithm can be described in terms of sinusoids:
  $$q_0=\frac{sin((1-T)\theta )}{sin(\theta )}q1+\frac{sin(T\theta )}{sin(\theta )}q2$$where $q_1$ and $q_2$ are normalized quaternions, and $\theta$ is half the angular distance between $q_1$ and $q_2$.

2. 问题

注意上面公式存在以下问题，需要在实现过程中考虑：

• 如果四元数点积的结果是负值（夹角大于90°），那么后面的插值就会在4D球面上绕远路。为了解决这个问题，先测试点积的结果，当结果是负值时，将两个四元数的其中一个取反（并不会改变它代表的朝向）。而经过这一步操作，可以保证这个旋转走的是最短路径。
• 当 $\mathbf{p}$ 和 $\mathbf{q}$ 的夹角 $\theta$ 差非常小时会导致 $\sin \theta \to 0$，这时除法可能会出现问题。为了避免这样的问题，当 $\theta$ 非常小时可以使用简单的线性插值代替 $(\theta \to 0$ 时，$\sin \theta \approx \theta )$，因此方程退化为线性方程：$\mathrm{slerp}(\mathbf{p},\mathbf{q},t)=(1-t)\mathbf{p}+t\mathbf{q}$