罗德里格旋转和李群、李代数的指数映射的关系

最新推荐文章于 2023-07-30 14:34:39 发布
最新推荐文章于 2023-07-30 14:34:39 发布
阅读量2.3k 收藏 11
点赞数 1
分类专栏： 算法 文章标签： 罗德里格 李群 李代数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/u014313096/article/details/86352608
版权
本文探讨了罗德里格旋转公式的几何意义，通过图解证明展示了如何从旋转轴和角度计算旋转后的向量。进一步解释了罗德里格公式与SO(3)李群的指数坐标之间的关系，指出两者在数学表达上的等价性，从而揭示了不同数学概念间的内在联系。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

        先来说一下罗德里格公式的作用：已知一向量，知道旋转轴和旋转角度，可求得旋转后的向量。简单地说，知道旋转轴和旋转角度，可以求得旋转矩阵。

        接下来用图解方式，给出罗德里格旋转公式的证明（理解证明，对矩阵、向量、叉乘、点乘的几何意义会有质的提高）

                               

        恩，接下来对这张大图，进行下分析：已知一向量p，知道旋转轴u(满足范数为1，即单位矢量)，旋转角度\phi。接下来对图中的标号做一下分析：

  1. 右上角蓝色的（p.u）代表p与u的内积，（p.u）u代表向量p在旋转轴上的投影，即如果把u比作z轴，则（p.u）代表向量p的z坐标的大小。
  2. p-(p.u)u则可以比作向量p在垂直于z轴（u）的平面上的投影，该平面上的投影矢量为v
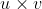
  3. u\times v
最低0.47元/天 解锁文章
C++ 李群 李代数库 sophus 使用
万有文的博客
01-06 6146
* sophus 库安装 * 本库为来版本 非模板的版本 * git clone https://github.com//strasdat/Sophus.git * git checkout a621ff 版本 * 在cmake编译 mkdir build
借助李群李代数完成对位姿的求导计算
weixin_41855010的博客
08-29 2407
一、对位姿求导数的意义 我们在对机器人进行位姿估计时的目标函数如下： 为了能取到损失函数J的最小值，我们需要对目标函数关于变换矩阵T求导数，我们可以不严谨非正式地记为如下表达式： 然而，变换矩阵T，包括其中的重要组成部分旋转矩阵R，都不满足对加减法的封闭，因此我们需要采用新的方法，那就是引入李群和李代数。 二、SO(3)李群和so(3)李代数 满足CAI2性质（Closure, Associativity, Identity-element, Inversible）的集合与运算的代数结构称为群。我们知道
SLAM中旋转向量（旋转轴/旋转角）、旋转矩阵、四元数、李代数的相互转化（附C++ Eigen库代码实例）
qq_41816368的博客
11-09 3137
SLAM中基本概念：旋转向量、旋转矩阵、四元数、李群、李代数的理解
李代数
juzi5211314的博客
02-05 3664
一、为啥需要李代数 假设拿相机一边移动一边拍摄，某个时刻相机位姿T，相机观察到一个世界坐标系中的空间点p，相机产生了一个观测数据z，那么： ...
李群与李代数一（定义与映射）
weixin_37781153的博客
09-21 440
为什要使用？ SLAM中，位姿是未知的，需要求出最符合当前状态的位姿！ 因为旋转矩阵本身具有约束的（正交且行列式的值为1），需要通过李群代数把位姿估计变成无约束问题 群 特殊正交群(对乘法是封闭的[即乘法的结果仍属于该集合])SO(3)={R∈R3×3∣RRT=I,det(R)=1}SO(3)=\{R\in R^{3×3}|RR^T=I,det(R)=1\}SO(3)={R∈R3×3∣RRT=I,det(R)=1} 特殊欧氏群(对乘法是封闭的[即乘法的结果仍属于该集合])SO(3)={T=[Rt0T1]T
旋转矩阵李代数的推导——旋转矩阵的李代数向量对应着旋转矩阵的旋转向量吗
sinat_19868271的博客
12-16 488
转载https://www.jianshu.com/p/345d0ece5005
视觉SLAM十四讲学习笔记-第四讲-李群与李代数基础和定义、指数和对数映射
weixin_36773706的博客
11-25 1102
基础： 在SLAM中的旋转，除了表示之外，我们还要对它们进行估计和优化。因为在SLAM中位姿是未知的，而我们需要解决什么样的相机位姿最符合当前观测数据这样的问题。一种典型的方式是把它构建成一个优化问题，求解最优的R, t，使得误差最小化。旋转矩阵自身是带有约束的（正交且行列式为1）。它们作为优化变量时，会引入额外的约束，使优化变得困难。通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。 三维旋转矩阵构成了特殊正交群 SO(3)，而变换矩阵构成了特殊欧氏群 SE(3)。
python中欧拉-罗德里格斯的代码详解
weixin_41855010的博客
07-21 1368
我们可以在python中定义以下函数来完成三维和四维的罗德里格斯公式的数值计算，即统一了旋转运动和一般螺旋运动的Euler-Rodrigues公式：R=eθAs=I+sinθAs+(1−cosθ)As2\mathbf R=e^{\theta \mathbf As} = \mathbf I + sin\theta \mathbf A_s + (1-cos\theta)\mathbf A_s^2R=eθAs=I+sinθAs​+(1−cosθ)As2​H=eθEs=I+sinθEs+(1−cosθ)Es2\ma
视觉SLAM十四讲第四讲
weixin_40486179的博客
10-14 398
第四章 李群与李代数 主要目标 理解李群与李代数的概念，掌握 SO(3), SE(3) 与对应李代数的表示方式。 理解 BCH 近似的意义。 学会在李代数上的扰动模型。 使用 Sophus 对李代数进行运算。 旋转矩阵自身是带有约束的（正交且行列式为 1）。它们作为优化变量时，会引入额外的约束，使优化变得困难。通过李群—李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。 一、李群与李代数基础 说三维旋转矩阵构成了特殊正交群 SO(3)，而变换矩阵构成了特殊欧氏群 SE(3)。它们写
通俗易懂！视觉slam第六部分——旋转向量，欧拉角
kaggle expert，全球排名前1000，清华计算机研究生，兴趣算法工程
02-20 1607
矩阵表示方式还有很多缺点： 1.SO(3) 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。同理，变换矩阵用十六个量表达了六自由度的变换。 2.旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为 1。变换矩阵也是如此。当我们想要估计或优化一个旋转矩阵/变换矩阵时，这些约束会使得求解变得更困难。 对于坐标系的旋转，我们知道，任意旋转都可以用一个旋转轴和一个旋转角来刻...
三维旋转、李群与李代数的一些知识点记录汇总
moumde的博客
10-23 3160
三维刚体运动、李群与李代数的一些知识点记录一、三维刚体旋转1.1 内积和外积1.2 旋转矩阵、变换矩阵和旋转向量1.2.1 旋转矩阵1.2.2 变换矩阵1.2.3 旋转向量1.3 欧拉角和四元数和姿态解算二、李群与李代数 以下内容来源于《视觉SLAM十四讲》以及其他博文内容的汇总，所有出处均会表明。部分内容比较简略，因为写本文的目的是仅做自身学习记录用途，好记性不如烂笔头，方便自己回顾（之前都学过但是现在发现忘得差不多了...），当然如果对大家有帮助那再好不过。 一、三维刚体旋转 1.1 内积和外积
知识点记录：李群李代数，微分流形，微分几何，图论
FL1717的博客
11-13 1930
在数学中，李群（Lie group）是具有群结构的实流形或者复流形，并且群中的加法运算和逆元运算是流形中的解析映射。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。微分流形（differentiable manifold），也称为光滑流形（smooth manifold），是拓扑学和几何学中一类重要的空间，是带有微分结构的拓扑流形。或者复流形，并且群中的加法运算和逆元运算是流形中的解析映射。
李代数与李群间的转换-指数映射、对数映射
weixin_44197735的博客
07-01 3009
李群和李代数转换，指数映射与对数映射，详细推导。
李群和李代数（一）——李群李代数的引出及其指数映射
qq_46067306的博客
07-30 1036
李代数有一个集合V\mathbb{V}V、一个数域F\mathbb{F}F和一个二元运算[，]组成，如果满足以下几条性质，则称（V\mathbb{V}VF\mathbb{F}F，[，]）为一个李代数，记作g。1.封闭性∀XY∈VXY∈V∀XY∈VXY∈V2.双线性∀XYZ∈Vab∈F∀XYZ∈Vab∈F有 [aX+bY,Z]=a[X,Z]+b[Y,Z]，[Z,aX+bY]=a[Z,X]+b[Z,Y]3.自反性∀。
李群与李代数基础
热门推荐
weixin_39568744的博客
07-12 2万+
最近在学习slam时第一次遇到李群与李代数的概念，由于一开始不太理解，所以想通过这篇笔记来重新归纳梳理一下。1.李群的概念：李群是具有连续（光滑）性质的群；它既是群也是流行；直观上看，一个刚体能够连续的在空间中运动，故SO（3）和SE（3）都是李群。（注：SO(3)是特殊正交群 SE(3)是特殊欧式群，由于旋转矩阵R是3乘3的维度，但自由度的约束只有3个自由度，所以旋转矩阵R在9维空间中是一个连续...
李群、李代数只求理解不求数学推导
三眼二郎
07-19 5140
群：集合+运算（G,·） 在近世代数中多次出现的概念，定义为“一种集合加上一种运算的代数结构”，运算需要满足封闭性，结合律，幺元，逆。群结构可以保证在群概念下的运算具有良好的性质。 知乎大佬讲解： https://www.zhihu.com/question/23091609 https://mp.weixin.qq.com/s/sVjy9kr-8qc9W9VN78JoDQ 这里二郎的理解（非数学...
VSlam十四讲中李代数相关公式推导
Coderii的博客
04-06 773
VSlam十四讲中李代数相关公式推导
视觉SLAM十四讲笔记-第四讲 李群与李代数
m0_55941084的博客
01-18 1517
目录 前提摘要： 一、群 1.1注意对象不同 1.2 概念 二、李群与李代数 2.1 李群 （Lie Group) 2.2 李代数 三、指数映射和对数映射 3.1 李代数so(3)指数映射 3.2 se(3)到SE(3)的指数映射： 3.3 对数映射 3.4 小结 四、求导与扰动模型（偏向于扰动模型） 公式汇总 五、实践：Sophus库 前提摘要： Question:当相机位姿不太准确的时候，我们如果对位姿进行微调呢？ 观测量即为R、t 或 T: 当R、t估计值不够
罗德里格斯公式Rodrigues' rotation formula推导
我不是斗哥的博客
02-17 4373
matlab 罗德里格旋转矩阵
最新发布
10-19
罗德里格旋转矩阵是一种将旋转向量转换为旋转矩阵的方法。在Matlab中，可以使用rodrigues函数来计算罗德里格旋转矩阵。该函数的语法如下： R = rodrigues(r) 其中，r是一个3x1的旋转向量，R是一个3x3的旋转矩阵。...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值