文章目录
本文代码, 见github; 如果您有任何疑问或者建议,请在文后留言。谢谢!
第五章:ESKF推导
一、目标
使用error-state滤波方法优点
二、Error-State 卡尔曼滤波
把传统的状态量分为了三部分:(真实状态)true state, (名义状态)nominal state, (误差状态)error state.
ESKF主要的思想是:名义状态使用非线性的方式进行积分(无近似误差),误差状态使用线性的方式积分(有近似误差),但是和传统卡尔曼比起来,这个线性化误差会小一些。
三、系统运动学(连续)
系统涉及到的变量如下:
| 真实状态 | 名义状态 | 误差状态 | 组合关系 | 观测量 | 噪声 | |
|---|---|---|---|---|---|---|
| 全部状态 | x t x_t xt | x x x | δ x \delta x δx | x t = x ⊕ δ x x_t = x\oplus \delta x xt=x⊕δx | ||
| 位置P | p t p_t pt | p p p | δ p \delta p δp | p t = p + δ p p_t = p + \delta p pt=p+δp | ||
| 速度v | v t v_t vt | v v v | δ v \delta v δv | v t = v + δ v v_t = v + \delta v vt=v+δv | ||
| 加速度a | a t a_t at | a m = a t + a n a_m = a_t + a_n am=at+an | a m a_m am | a n a_n an |
需要注意的是,在组合关系中,状态变量中的都是真值=名义状态+误差状态,而测量值中,测量值=真值+噪声,在实际使用过程中,不要弄混淆了。
1. 真实状态运动学
p t ˙ = v t v t ˙ = a t = a m − a n \dot{p_t} = v_t \\ \dot{v_t} = a_t = a_m - a_n pt˙=vtvt˙=at=am−an
2. 名义状态运动学
在定义名义状态时,我们可以不考虑噪声与扰动
p ˙ = v v ˙ = a m \dot{p} = v \\ \dot{v} = a_m p˙=vv˙=am
从这里可以看出,这里直接使用了加速度的观测值。
3. 误差状态运动学
因为已经定义好了真实状态与名义状态,根据表中的关系,我们直接可以得到误差状态运动学
δ p ˙ = δ v δ v ˙ = − a n \dot{\delta p} = \delta v\\ \dot{\delta v} = -a_n δp˙=δvδv˙=−an
四、系统运动学(离散)
1. 名义状态运动学
p ← p + v Δ t + 0.5 a m Δ t 2 v ← v + a m Δ t p \leftarrow p + v\Delta t+0.5a_m\Delta t^2 \\ v \leftarrow v + a_m\Delta t p←p+vΔt+0.5amΔt2v←v+amΔt
对于p来说,是根据连续状态下名义状态运动学公式来的,首先对v积分,因为v是变化的,还要对v的变化进行二次积分。用求面积的公式来举一个例子如下:
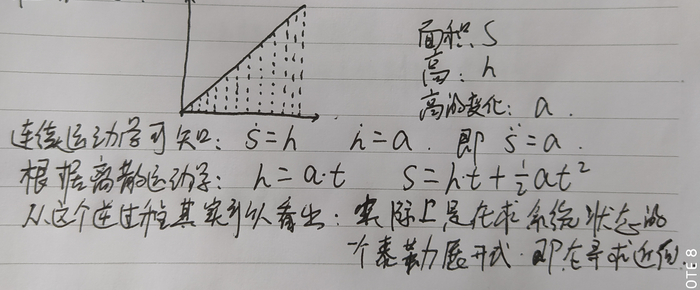
名义状态实际上就是测量状态,是包含噪声的 a m = a t + a n a_m = a_t + a_n am=at+an。
2. 误差状态运动学
δ
p
←
δ
p
+
δ
v
δ
t
δ
v
←
δ
v
+
v
i
\delta p \leftarrow \delta p + \delta v \delta t \\ \delta v \leftarrow \delta v + v_i
δp←δp+δvδtδv←δv+vi
可以看出名义状态运动学考虑了非线性部分,而误差状态运动学直接是线性关系。前面的
a
n
a_n
an这里直接变成了
v
i
v_i
vi., 也可以看出,名义状态考虑了二阶,而误差状态考虑了一阶。
3. 误差状态雅克比矩阵与扰动方程
这里写成紧凑形式 δ x = [ δ p ; δ v ] T \delta x = [\delta p; \delta v]^T δx=[δp;δv]T,然后利用误差运动学方程,得到线性化,得到状态转移函数。如上:
F = [ I Δ t 0 I ] F = \left[ \begin{matrix} I & \Delta t\\0&I \end{matrix}\right] F=[I0ΔtI]
第六章:IMU与其他传感器融合
在一个设计良好的系统中,当GPS信号过来的时候,应该要能修正IMU的bias. 主要步骤有三步:
- 误差状态的观测滤波
- 将误差状态赋值到名义状态
- 误差状态的重置
一、误差状态的观测
首先GPS的观测与状态的关系是: y = h ( x t ) + v y = h(x_t) + v y=h(xt)+v. 在这里y就是一个1维的观测。 x t x_t xt是真值状态。
然后卡尔曼增益与传统的一样,状态量的更新不太不一样:
δ x ← K ( y − h ( x t ) ) \delta x \leftarrow K(y-h(x_t)) δx←K(y−h(xt))
当然,上式符合直观理解,当真实状态与观测值一致时,误差状态的修正量就是0。当y较大时, δ x \delta x δx就会大于0。
通过位置观测的方差可知:
V = Σ s n V = \Sigma_{sn} V=Σsn
1、雅克比矩阵
通过真值状态、名义状态、误差状态定义可知:
h ( x t ) = x t = p + δ p h(x_t) = x_t = p + \delta p h(xt)=xt=p+δp
进一步可知:
H = [ 1 , 0 ] H = [1, 0] H=[1,0]
二、误差状态插入到名义状态
本质就是让名义状态等于真实状态,即名义状态的更新操作
x ← x ⊕ δ x ^ x \leftarrow x \oplus \hat{\delta x} x←x⊕δx^
三、ESKF重置
因为误差状态已经在前面插入到了名义状态中,这里肯定需要将误差状态置为0。同时,因此置零的原因,需要将协方差也更新一下。对于当前的位置估计来说,只需要将误差状态置为0,协方差矩阵不用更新了。
四、仿真
1. 仿真数据生成
假设运动物体沿着x轴运动:
s g t = s i n ( m ∗ t ) + c o s ( n ∗ t ) v g t = m ∗ c o s ( m ∗ t ) − n ∗ s i n ( n ∗ t ) a g t = − m 2 ∗ s i n ( m ∗ t ) − n 2 ∗ c o s ( n ∗ t ) s_{gt} = sin(m*t) + cos(n*t) \\ v_{gt} = m*cos(m*t) - n*sin(n*t) \\ a_{gt} = -m^2*sin(m*t) - n^2*cos(n*t) sgt=sin(m∗t)+cos(n∗t)vgt=m∗cos(m∗t)−n∗sin(n∗t)agt=−m2∗sin(m∗t)−n2∗cos(n∗t)
这里用 a g t + a n a_{gt} + a_n agt+an来模拟实际测量的加速度值,其中 a n ∼ N ( 0 , Σ a n ) a_n \sim N(0, \Sigma_{an}) an∼N(0,Σan)设计为一个白噪声。用 s g t + s n s_{gt} + s_n sgt+sn来模拟绝对位置观测,其中 s n ∼ N ( 0 , Σ s n ) s_n \sim N(0, \Sigma_{sn}) sn∼N(0,Σsn)也为一个白噪声。以下为纯积分推算:

如上图所示,依次为:位置、加速度、位置预测、速度预测。
2. ESKF滤波
代码实现了两个简单的滤波:ESKF与EKF,下图所示为ESKF滤波的结果与观测数据、真值数据的对比:


下图所示为EKF与ESKF之间的对比:

从目前的结果还并不能明显得出: ESKF比EKF好的这个结论;
参考
- Quaternion kinematics for the error-state Kalman filter.pdf 链接: https://pan.baidu.com/s/1pk5esPGVNSiSLyWdlXVBeA 提取码: vzcw
- MSCKF那些事(四)算法详解2:数学基础 这里面说了几种协方差更新的形式,对应着不同的正定状态。
- ESKF的一些理解

























 1841
1841

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










