跟着iMeta学做图｜NMDS分析展示群落beta多样性

最新推荐文章于 2023-08-28 00:50:59 发布
最新推荐文章于 2023-08-28 00:50:59 发布
阅读量8.3k 收藏 53
点赞数 7
文章标签： 算法 python 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/woodcorpse/article/details/128030062
版权

原始教程链接：https://github.com/iMetaScience/iMetaPlot/tree/main/221108NMDS

写在前面

非度量多维尺度分析(Non-metric multidimensional scaling, NMDS)，是基于相异矩阵或距离矩阵进行排序分析的间接梯度分析方法，在微生物组研究中可以用来展示群落beta多样性。本期我们挑选2022年2月24日刊登在iMeta上的Linking soil fungi to bacterial community assembly in arid ecosystems - iMeta：西农韦革宏团队焦硕等-土壤真菌驱动细菌群落的构建，选择文章的Figure 6C进行复现，基于vegan包，讲解和探讨和NMDS分析和可视化的方法，先上原图：

06a030d4a7e6b0b1c88baeb80b2c459f.gif

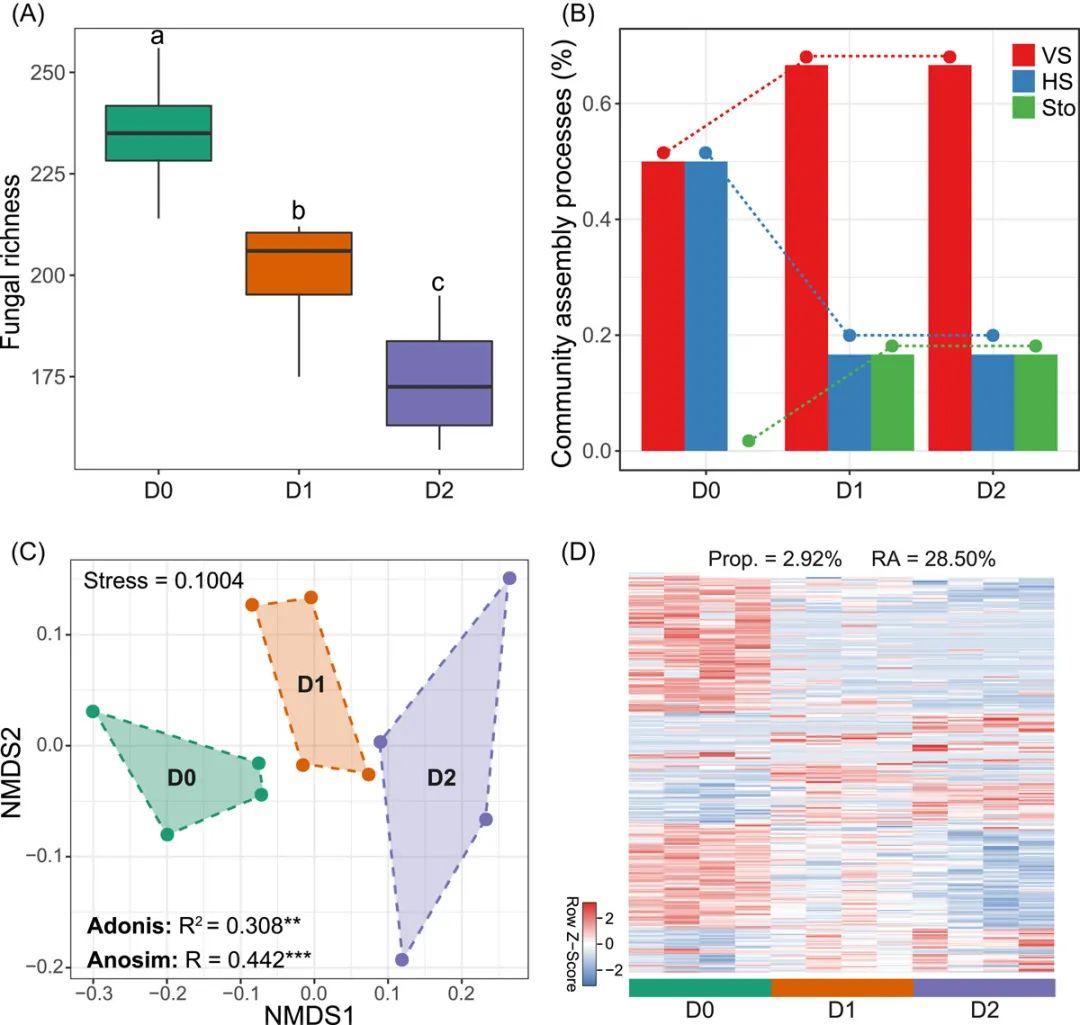
c9284f6f8b05267c3c73b3c83ac278f0.jpeg

接下来，我们将通过详尽的代码逐步拆解原图，最终实现对原图的复现。代码编写及注释：农心生信工作室。

R包检测和安装

01

安装核心R包vegan以及ggplot2，并载入所有R包。

if (!require("vegan"))
  install.packages('vegan')
if (!require("ggplot2"))
  install.packages('ggplot2') 
# 加载包
library(vegan)
library(ggplot2)

生成测试数据

02

由于缺少原始数据，因此本例使用vegan包自带的dune数据集进行测试。dune包含了20个样品，每个样品有30个物种丰度，每一行是一个样品，每一列是一个物种。

# 载入dune数据集
data(dune)
#载入dune包含分组信息等的元数据（即metadata），分组信息为Management列
data(dune.env)

NMDS分析

03

获取数据后，即可利用vegan包进行NMDS分析。

#计算bray_curtis距离
distance <- vegdist(dune, method = 'bray')
#NMDS排序分析，k = 2预设两个排序轴
nmds <- metaMDS(distance, k = 2)
#> Run 0 stress 0.1192678 
#> Run 1 stress 0.1192678 
#> ... Procrustes: rmse 4.495733e-05  max resid 0.0001375161 
#> ... Similar to previous best
#> Run 2 stress 0.1183186 
#> ... New best solution
#> ... Procrustes: rmse 0.02026799  max resid 0.06495211 
#> Run 3 stress 0.1183186 
#> ... New best solution
#> ... Procrustes: rmse 1.832694e-05  max resid 5.57604e-05 
#> ... Similar to previous best
#> Run 4 stress 0.1809577 
#> Run 5 stress 0.1192678 
#> Run 6 stress 0.1183186 
#> ... New best solution
#> ... Procrustes: rmse 5.582524e-06  max resid 1.803473e-05 
#> ... Similar to previous best
#> Run 7 stress 0.1192678 
#> Run 8 stress 0.1192678 
#> Run 9 stress 0.1192678 
#> Run 10 stress 0.1192678 
#> Run 11 stress 0.1192679 
#> Run 12 stress 0.1808911 
#> Run 13 stress 0.1192678 
#> Run 14 stress 0.1183186 
#> ... Procrustes: rmse 5.943311e-06  max resid 1.823899e-05 
#> ... Similar to previous best
#> Run 15 stress 0.1886532 
#> Run 16 stress 0.1192678 
#> Run 17 stress 0.1183186 
#> ... Procrustes: rmse 3.001088e-06  max resid 9.607646e-06 
#> ... Similar to previous best
#> Run 18 stress 0.1192679 
#> Run 19 stress 0.1808911 
#> Run 20 stress 0.1183186 
#> ... Procrustes: rmse 2.027412e-05  max resid 6.520856e-05 
#> ... Similar to previous best
#> *** Best solution repeated 4 times
#查看结果
#summary(nmds)

04

获取可视化所需数据。

#获得应力值（stress）
stress <- nmds$stress
#将绘图数据转化为数据框
df <- as.data.frame(nmds$points)
#与分组数据合并
df <- cbind(df, dune.env)

NMDS可视化

05

根据分组绘制一个最基础的散点图。

p <- ggplot(df, aes(MDS1, MDS2))+
  geom_point(aes(color = Management), size = 5)

387533c34cf3ab0383f61439f6a69fdc.png

06

我们注意到，原图中，每个分组被连接成不规则的多边形并用不同颜色表示，我们可以通过ggplot2中geom_polygon()来绘制。geom_polygon()会按照数据中出现的顺序连接观测值，内部可填充颜色。

p <- ggplot(df, aes(MDS1, MDS2))+
  geom_point(aes(color = Management), size = 5)+
  geom_polygon(aes(x = MDS1, y = MDS2, fill = Management, group = Management, color = Management),
               alpha = 0.3, linetype = "longdash", linewidth = 1.5) #通过按顺序连接观测值绘制多边形

d5470402da1fa020ca9773d57fa5bcb6.png

07

由于geom_polygon()会按照数据中出现的顺序连接观测值，因此如果我们按照df自身顺序来绘制多边形，多边形会非常奇怪，没法代表不同分组。因此，我们需要预先处理df的顺序，按合理的顺序连接观测值。

df <- df[order(df$Management), ]#先按分组排序
df$Order <- c(2, 1, 3, 1, 2, 3, 4, 5, 3, 5, 1, 6, 2, 4, 1, 2, 6, 3, 5, 4)#添加一列Order，给每个分组内观测点的手动排序
df <- df[order(df$Management, df$Order), ]#按分组和Order排序
p <- ggplot(df, aes(MDS1, MDS2))+
  geom_point(aes(color = Management), size = 5)+
  geom_polygon(aes(x = MDS1, y = MDS2, fill = Management, group = Management, color = Management),
               alpha = 0.3, linetype = "longdash", linewidth = 1.5)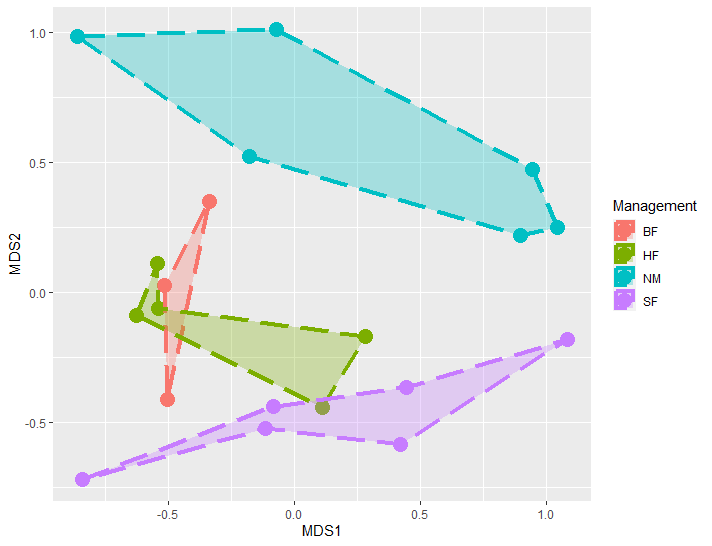

978ffe1ff61a798223b739df8041899c.png

08

分别进行Anosim分析（Analysis of similarities）和PERMANOVA（即adonis）检验分析。

#设置随机种子
set.seed(123)
#基于bray-curtis距离进行PERMANOVA分析
adonis <-  adonis2(dune ~ Management, data = dune.env, permutations = 999, method = "bray")
#基于bray-curtis距离进行anosim分析
anosim = anosim(dune, dune.env$Management, permutations = 999, distance = "bray")

09

美化图片，并用AI微调。

# 应力值stress，Adonis R2与显著性，Anosim R与显著性
stress_text <- paste("Stress  =", round(stress, 4))
adonis_text <- paste(paste("Adonis  =", round(adonis$R2, 2)), "**")[1]
anosim_text <- paste(paste("Anosim  =", round(anosim$statistic, 2)), "**")


p <- ggplot(df, aes(MDS1, MDS2))+
  geom_point(aes(color = Management), size = 5)+
  geom_polygon(aes(x = MDS1, y = MDS2, fill = Management, group = Management, color = Management), alpha = 0.3, linetype = "longdash", linewidth = 1.5)+
  theme(plot.margin = unit(rep(1, 4), 'lines'), 
        panel.border = element_rect(fill = NA, color = "black", size = 0.5, linetype = "solid"), 
        panel.grid = element_blank(), 
        panel.background = element_rect(fill = 'white'))+
  guides(color = "none", fill = "none")+
  ggtitle(paste(paste(stress_text, adonis_text), anosim_text))

37764bffd552f1a983215fd623dab116.jpeg

完整代码

if (!require("vegan"))
  install.packages('vegan')
if (!require("ggplot2"))
  install.packages('ggplot2') 
# 加载包
library(vegan)
library(ggplot2)
 
# 载入dune数据集
data(dune)
#载入dune包含分组信息等的元数据（即metadata），分组信息为Management列
data(dune.env)
#计算bray_curtis距离
distance <- vegdist(dune, method = 'bray')
#NMDS排序分析，k = 2预设两个排序轴
nmds <- metaMDS(distance, k = 2)
#> Run 0 stress 0.1192678 
#> Run 1 stress 0.1192678 
#> ... Procrustes: rmse 1.505128e-05  max resid 4.673581e-05 
#> ... Similar to previous best
#> Run 2 stress 0.1192678 
#> ... Procrustes: rmse 3.715749e-06  max resid 1.009651e-05 
#> ... Similar to previous best
#> Run 3 stress 0.1889642 
#> Run 4 stress 0.1192679 
#> ... Procrustes: rmse 0.0001542849  max resid 0.0004702712 
#> ... Similar to previous best
#> Run 5 stress 0.1886532 
#> Run 6 stress 0.2341212 
#> Run 7 stress 0.1192678 
#> ... Procrustes: rmse 1.328909e-05  max resid 4.273575e-05 
#> ... Similar to previous best
#> Run 8 stress 0.1886532 
#> Run 9 stress 0.1192678 
#> ... Procrustes: rmse 1.903819e-05  max resid 5.828243e-05 
#> ... Similar to previous best
#> Run 10 stress 0.1192678 
#> ... Procrustes: rmse 6.358457e-06  max resid 1.687026e-05 
#> ... Similar to previous best
#> Run 11 stress 0.119268 
#> ... Procrustes: rmse 5.501506e-05  max resid 0.0001605112 
#> ... Similar to previous best
#> Run 12 stress 0.1192678 
#> ... New best solution
#> ... Procrustes: rmse 5.074111e-06  max resid 1.393603e-05 
#> ... Similar to previous best
#> Run 13 stress 0.1192678 
#> ... Procrustes: rmse 3.160318e-05  max resid 9.85043e-05 
#> ... Similar to previous best
#> Run 14 stress 0.1886532 
#> Run 15 stress 0.2003486 
#> Run 16 stress 0.2035424 
#> Run 17 stress 0.1192678 
#> ... Procrustes: rmse 2.440829e-05  max resid 7.079487e-05 
#> ... Similar to previous best
#> Run 18 stress 0.1183186 
#> ... New best solution
#> ... Procrustes: rmse 0.02027171  max resid 0.06497302 
#> Run 19 stress 0.1183186 
#> ... New best solution
#> ... Procrustes: rmse 3.78469e-06  max resid 9.699447e-06 
#> ... Similar to previous best
#> Run 20 stress 0.1192678 
#> *** Best solution repeated 1 times
#查看结果
#summary(nmds)
#获得应力值（stress）
stress <- nmds$stress
#将绘图数据转化为数据框
df <- as.data.frame(nmds$points)
#与分组数据合并
df <- cbind(df, dune.env)
df <- df[order(df$Management), ]#先按分组排序
df$Order <- c(2, 1, 3, 1, 2, 3, 4, 5, 3, 5, 1, 6, 2, 4, 1, 2, 6, 3, 5, 4)#添加一列Order，给每个分组内观测点的手动排序
df <- df[order(df$Management, df$Order), ]#按分组和Order排序
 
#设置随机种子
set.seed(123)
#基于bray-curtis距离进行PERMANOVA分析
adonis <- adonis2(dune ~ Management, data = dune.env, permutations = 999, method = "bray")
#基于bray-curtis距离进行anosim分析
anosim = anosim(dune, dune.env$Management, permutations = 999, distance = "bray")
 
# 应力值stress，Adonis R2与显著性，Anosim R与显著性
stress_text <- paste("Stress  =", round(stress, 4))
adonis_text <- paste(paste("Adonis  =", round(adonis$R2, 2)), "**")[1]
anosim_text <- paste(paste("Anosim  =", round(anosim$statistic, 2)), "**")
 
p <- ggplot(df, aes(MDS1, MDS2))+
  geom_point(aes(color = Management), size = 5)+
  geom_polygon(aes(x = MDS1, y = MDS2, fill = Management, group = Management, color = Management),
               alpha = 0.3, linetype = "longdash", linewidth = 1.5)+
  theme(plot.margin = unit(rep(1, 4), 'lines'), 
        panel.border = element_rect(fill = NA, color = "black", size = 0.5, linetype = "solid"), 
        panel.grid = element_blank(), 
        panel.background = element_rect(fill = 'white'))+
  guides(color = "none", fill = "none")+
  ggtitle(paste(paste(stress_text, adonis_text), anosim_text))


ggsave("Figure6C.pdf", p, height = 5.69, width = 7.42)

猜你喜欢

iMeta简介 高引文章 高颜值绘图imageGP 网络分析iNAP
iMeta网页工具 代谢组MetOrigin 美吉云乳酸化预测DeepKla
iMeta综述 肠菌菌群 植物菌群 口腔菌群 蛋白质结构预测

10000+：菌群分析 宝宝与猫狗 梅毒狂想曲 提DNA发Nature

系列教程：微生物组入门 Biostar 微生物组  宏基因组

专业技能：学术图表 高分文章 生信宝典 不可或缺的人

一文读懂：宏基因组 寄生虫益处 进化树 必备技能：提问 搜索  Endnote

扩增子分析：图表解读 分析流程 统计绘图

16S功能预测   PICRUSt  FAPROTAX  Bugbase Tax4Fun

生物科普:  肠道细菌 人体上的生命 生命大跃进  细胞暗战 人体奥秘  

写在后面

为鼓励读者交流快速解决科研困难，我们建立了“宏基因组”讨论群，己有国内外6000+ 科研人员加入。请添加主编微信meta-genomics带你入群，务必备注“姓名-单位-研究方向-职称/年级”。高级职称请注明身份，另有海内外微生物PI群供大佬合作交流。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍未解决群内讨论，问题不私聊，帮助同行。

点击阅读原文，跳转最新文章目录阅读

刘永鑫Adam
关注
可视化绘图技巧100篇分析篇（一）-数据降维NMDS分析（补充篇）
getusushu的博客
05-08 1559
非度量多维尺度法[1]是一种将多维空间的研究对象（样本或变量）简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法。适用于无法获得研究对象间精确的相似性或相异性数据，仅能得到他们之间等级关系数据的情形。其基本特征是将对象间的相似性或相异性数据看成点间距离的单调函数，在保持原始数据次序关系的基础上，用新的相同次序的数据列替换原始数据进行度量型多维尺度分析。
非度量多维排列 NMDS (Non-metric multidimensional scaling)分析
悟道西方
10-09 1万+
多维排列 (Multidimensional scaling,MDS)是可视化多变量样品(如多个物种丰度、多个基因表达)相似性水平的一种方法。其基于距离矩阵进行一系列的排序分析。经典的MD...
生信学习-高通量分析-NMDS分析: 非度量多维尺度分析
热门推荐
weixin_53819139的博客
02-26 4万+
NMDS分析: 非度量多维尺度分析（Non-metric multidimensional scaling,NMDS）是一种将多维空间的研究对象简化到低维空间进行定位，分析和归类，同时又保留对象间原始关系的数据分析方法。一般用组间样本的秩次（数据排名rank order）上的差异来定义距离。 NMDS图形常用作微生物群落研究的β分析。 NMDS侧重反映距离矩阵中数值的排序关系，弱化数值的绝对差异程度。在多样本、物种数量多的情况下（相对于数值间的差异，可进行排序的数量更大），NMDS模型能更准确地反映出距离矩
利用NMDS对药物处理下肠道菌群微生物群落多态性分析
qq_43337249的博客
05-12 4321
title: “利用NMDS对药物处理下肠道菌群微生物群落多态性分析” NMDS过程是迭代的，按照以下的workflow进行操.
1、NMDS非度量多维尺度分析作图（R）
weixin_65283273的博客
07-16 1102
【代码】1、NMDS非度量多维尺度分析作图（R）
在线作图丨数据降维分析④——NMDS分析
weifanbio的博客
07-26 8212
Question 1：什么是NMDS分析？ 非度量多维标度（Non-metric Multidimensional Scaling，NMDS）是一种将多维空间的研究对象（样本或变量）简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法。 Question 2：NMDS与其他降维方式有什么区别？ PCA基于线性模型，仅适用于物种少，环境因素、物种丰度波动变化小的情况。PCoA与NMDS用于反映样本距离矩阵关系，不同点在于NMDS更侧重反映距离矩阵中数值的排序关系，弱化数值的绝对差异程度。
使用R，ggplot2绘制NMDS图
weixin_38605247的博客
12-05 2万+
使用R，ggplot2绘制NMDS图 输入文件准备 mapping.txt ：样品名与分组信息 otu.txt : otu表 文件下载 : https://github.com/tangshanshaolu/R_test.git 代码部分 library(vegan) library(ggplot2) pdf("nmds.pdf") otu<-read.table("otu.txt",heade
"群落Beta多样性排序分析的详细介绍及应用
综上所述，beta 多样性(PCoA/NMDS)排序分析在生态学研究中扮演着不可或缺的角色，可以帮助研究人员深入了解群落之间的相似性和差异性，揭示物种组成的变化规律，为生态系统的保护和管理提供重要的科学依据。...
图表复现|PRD地下水微生物群落的多样性分析文献
weifanbio的博客
10-07 979
前言 之前有小伙伴问道，能否复现一篇关于微生物多样性文献里的图片，今天小编给大家分享一下微生物分析相关的画图方法。这篇文献《Diversity and predictive metabolic pathways of the prokaryotic microbial community along a groundwater salinity gradient of the Pearl River Delta, China》旨在研究珠三角地区地下水的微生物群落结构。 期刊名称：scientificrepo
Beta多样性分析：一句代码搞定CCA、DCA、DPCoA、MDS、NMDS、PCoA、RDA
a852232394的博客
06-13 2456
大家好，今天我将介绍如何使用R语言phyloseq包进行常见的beta多样性分析，并使用ggplot2包进行绘图展示。
SDR 单纯形计算：物种丰富度中 beta 多样性、嵌套性和一致性的可视化-matlab开发
05-30
物种丰富度中 beta 多样性、嵌套性和一致性的可视化-matlab开发"涉及到的是生物多样性的研究领域，特别关注生态学中的物种丰富度（Species Diversity）以及如何通过计算和可视化来理解和分析这种多样性。在这个主题...
nmds与mds的区别_数量生态学笔记||非约束排序|NMDS
weixin_39617044的博客
12-31 1151
非度量多维尺度分析(Non-metric multidimensional scaling,NMDS)是间接梯度分析方法，其基于距离或不相似矩阵产生排序。与尝试最大化排序中的对象之间的方差或对应关系的方法不同，NMDS试图尽可能接近地表示低维空间中的对象之间的成对不相似性。可以使用任何相异系数或距离度量来构建用作输入的距离矩阵。NMDS是一种基于排名的方法。这意味着原始距离数据被等级替换。因此，对...
R统计绘图-NMDS、环境因子拟合(线性和非线性)、多元统计(adonis2和ANOSIM)及绘图(双因素自定义图例)
qq_39859424的博客
02-23 4138
在PCA、PCoA、CA和NMDS非约束排序方法中，只有NMDS不是基于特征向量的排序方法，不会最大化排序轴所代表的变量方差(可旋转轴，达到PCA的效果，PC1代表最大方差)。书中提到PCoA等的排序结果，可以作为NMDS的输入，用于将超过2-3D的数据空间，在2-3D的维度展示出来。)提到“NMDS分析对0值不太敏感，即使有较多的0，也可以得到较为稳健的结果”。如果拿不准要选择那种转换方法和距离指数，就在满足分析假设的前提下，把所有分析都做一遍，选择分析效果更好的方法就行，不要让自己陷入纠结，浪费时间。
非度量多维标度_16s分析作图之NMDS非度量多维尺度分析
weixin_39844267的博客
12-21 4192
摘要：beta多样性分析网络上已经有很多，大部分出图都是基于R的基础包，很难看，而且很多图形不够完善，没有做方差分析，更没有将其直接输到图上，本文主要做NMDS分析并做一张完善的高质量图片，提取stress值，推荐适合NMDS结果的差异分析并通过命令展示在图形上，最后加上置信区间椭圆。NMDS分析，网络上已近有很多相关教程分享其原理，与其他排序(PCA、PCoA、CCA、RDA)方法的不同之处，简...
生物群落多样性——β多样性
m0_60609261的博客
08-27 1万+
生物群落多样性——β多样性
关于NMDS的一知半解
weixin_38605247的博客
12-05 1万+
最近阅读了一下NMDS的相关资料，自己梳理了一下并做出简要总结： NMDS的目的是想要把复杂的多维空间的点，降维后（通常是二伟）展示出来。 类似的降维展示有PCA，但是与PCA不同。 PCA是采用了欧氏距离（欧氏距离什么的我还不太懂，后续会继续研究，欢迎大 家和我讨论） NMDS 是依据排列顺序（rank order）来定义距离。 NMDS 的
ggplot2作图之NMDS图
weixin_45803246的博客
09-24 1027
NMDS作图
R语言绘制NMDS图
Mrrunsen的博客
01-31 2628
非度量多维标度（Non-metric Multidimensional Scaling，NMDS）是一种将多维空间的研究对象（样本或变量）简化到低维空间进行定位、分析和归类，同时又保留对象间原始关系的数据分析方法。 与PCoA相似，NMDS都使用样本相似性距离矩阵进行降维排序分析，但NMDS侧重反映距离矩阵中数值的排序关系，NMDS图形常用作微生物群落研究的β分析。 来看看R的vegan包和ggplot2包是如何绘制NMDS图的。 使用数据文件如下： ...
使用R语言绘制NMDS图
最新发布
ByteGlide的博客
08-28 1102
使用R语言绘制NMDS图NMDS（非度量多维尺度）是一种常用的多元统计方法，用于可视化和分析多变量数据的相似性或差异性。在R语言中，我们可以使用包来进行NMDS分析和绘图。下面我将为您提供详细的步骤和源代码。 准备数据 接下来，我们需要准备数据。NMDS图要求输入一个相异度矩阵或距离矩阵来表示样本间的相似性或差异性。您可以根据您的数据类型选择适当的距离度量方法，例如欧氏距离、曼哈顿距离等。假设您的数据存储在一个名为的数据框中，其中每一行代表一个样本，每一列代表一个变量。您可以使用以下代码计算距离矩阵：
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值