BP神经网络——从二次代价函数（Quadratic cost）到交叉熵（cross-entropy cost）代价函数

通过下文的阐述我们可以获得以下信息：

1. 反向传播（back propagation）算法是一个计算框架（或者计算流程）

   既然是一个计算框架，便与代价函数的具体形式（无论是二次代价还是交叉熵代价函数，只要能将预测的误差映射为一个标量，当然这一映射要满足特定的物理意义）无关。正因为如此，我们可将任何满足特定条件的代价函数embedded反向传播的计算过程。

2. 不同代价函数在计算上的不同

   不同代价函数的不同就在于step 2，计算单样本的预测误差对最后一层各神经元的输入（$z$）的微分（导数）形式不同，也即$\delta^L$不同。

我们首先来回顾BP神经网络反向传播过程：

I：前向计算各层各个神经元的输入与输出，并记录之

根据权重和偏置的初始化值前向计算（feedforward）各个layer的各个neuron的输入（又叫得分，score，对应于$z$）与输出（又叫激活值，activation，简记为$a$），下面给出向量的形式：

$$z^\ell=w^\ell\cdot a^{\ell-1}+b^\ell\\ a^\ell=\sigma(z^\ell)$$

II：反向传播的起点，计算最后一层的$\delta^L$

首先在当前网络状态（$(w,b)$给定）下，根据feedforward($a=\sigma(w\cdot a+b)$)，预测当前样本$x$的label值，再根据代价函数（此时不指定具体形式，$C=(a, y)$，$a=\sigma(z)$，$a$是activation激活值的缩写），计算对于神经网络的最后一层，代价函数关于最后一层的输入$z$的导数：

$$\delta^L=\frac{\partial\,C(a, y)}{\partial\,z^L}$$

$L$表示整个神经网络拓扑结构的层数，在代价函数为二次代价（Quadratic cost）的情况下：

$$C(a,y)=\frac12\|a-y\|^2=\frac12\|\sigma(z^L)-y\|^2\\ \delta^L=\frac{\partial\,C(a,y)}{\partial z^L}=(\sigma(z^L)-y)\cdot\sigma'(z^L)$$
代价函数为交叉熵（cross-entropy）的情形（$a=\sigma(z^L)$）：

$$\begin{split} C(a,y)&=-(y\ln(a)+(1-y)\ln(1-a))\\ \delta^L&=\frac{\partial\,C(a,y)}{\partial\,z^L}=-(\frac y{\sigma(z^L)}-\frac{1-y}{1-\sigma(z^L)})\cdot \sigma'(z^L) \end{split}$$
因为 $\sigma(z)=\frac1{1+\exp^{-z}}$，经过简单求导其关于 $z$的微分为：$\sigma'(z)=\sigma(z)(1-\sigma(z))$，进一步可将上式化简为：
$$\delta^L=-(y\cdot(1-\sigma(z^L))-(1-y)\cdot\sigma(z^L))=a^L-y$$

对比两种代价函数下的$\delta^L$，我们发现$\sigma'(z^L)$这一项神奇地消失了，有没有什么特殊的意义呢？
我们来观察$\sigma(z)=\frac1{1+\exp(-z)}$这一著名的sigmoid型函数：

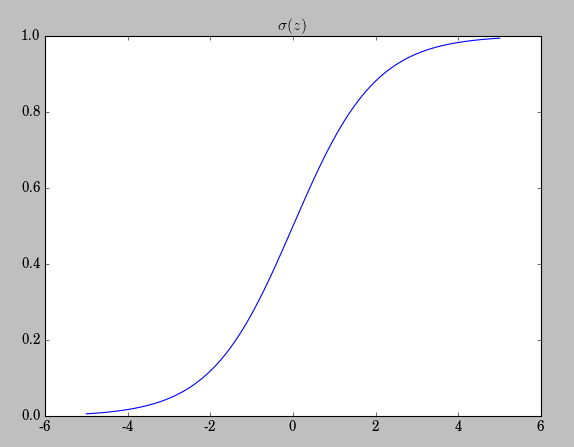
我们看到在 $\sigma(z)$逼近0或者1时，变化率（ $\sigma'(z)$）越来越小，呈现一种饱和状态（ saturation），当 $\sigma'(z)$变化率减慢，也就意味着 $\delta^L$变化率减慢，也就意味着学习率在下降（当然是在同等 $\mathrm{learning\,rate:\eta}$的前提下）。

所以，将代价函数换成交叉熵，便避免了因$\sigma'(z)$饱和而带来的学习率的下降的情况，当然这种替换仅对sigmoid型的激励函数有效。

III：反向传播，更新各层之间的权重与偏置

$$\frac{\partial\,C}{\partial\,w^\ell}=\frac{\partial\, C}{\partial\,z^\ell}\cdot \frac{\partial z^l}{\partial w^\ell}=\delta^\ell\cdot x^{\ell-1}$$

这里需要注意的是向量$\delta^\ell（这里为列向量）、x^{\ell-1}$（这里为行向量）以及权值更新矩阵$\frac{\partial\,C}{\partial\,w^\ell}$的size的问题，$(\frac{\partial\,C}{\partial\,w^\ell})_{j\times i}=(\delta^\ell)_{j\times 1}\times(x^{\ell-1})_{1\times i}$，编程时要特别注意。

反向传播算法的核心公式即是：

$$\delta^\ell=\frac{\partial\, C}{\partial\,z^\ell}=\frac{\partial\, C}{\partial\,z^{\ell+1}}\cdot \frac{\partial\,z^{\ell+1}}{\partial\,a^{\ell}}\cdot\frac{\partial\; a^{\ell}}{\partial z^{\ell}} =(\delta^{\ell+1}\cdot w^{\ell+1})\odot \sigma'(z^\ell)$$

这里矩阵和向量的size分别为：$(\delta^\ell)_{j}=((w^{\ell+1})_{k\times j}^T\times(\delta^{\ell+1})_{k\times 1})_{j}\odot\sigma'(z^\ell)_{j\times 1}$。$\odot$表示同size的矩阵或者向量进行按位相乘，计算十分简单，对应于matlab中的.*，numpy.ndarray的*，注意两种语言的差异。

而我们在step 2，已经计算过最末一层的$\delta^L$，由此从后向前便可计算各层的权值与偏置。

难能可贵的一点是：我们在步骤3并未看到任何与代价函数有关的记号，它已全部隐式的embedded在$\delta^\ell$中了。

下面给出先关的代码：

def sigmoid(z):
    return 1./(1.+np.exp(-z))
def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))

class QuadraticCost(object):
    @staticmethod
    def fn(a, y):
        return 1/2*np.linalg.norm(a-y)**2
    @staicmethod
    def delta(z, a, y):
        return (a-y)*sigmid_prime(z)

class CrossEntroyCost(object):
    @staticmethod
    def fn(a, y):
        # 为了数值稳定性，有可能出现（y=1，a=1）的情况，0*log(0)=nan
        # nan+任何值=nan，nan破坏最后的内积运算
        return -(np.dot(y.transpose(), np.nan_to_num(np.log(a)))+
                np.dot((1-y).transpose(), np.nan_to_num(np.log(1-a))))
    @staticmethod
    def delta(z, a, y):            # 保持接口一致
        return a-y

# 作为Network类的成员函数出现：
def backprog(self, x, y):
    nabla_b = [np.zeros(b.shape) for b in self.biases] 
    nabla_w = [np.zeros(w.shape) for w in self.weights]

    activation = x
    activations = [x]
    zs = []
    # step 1
    for w, b in zip(self.weights, self.biases):
        z = np.dot(w, activation) + b
        zs.append(z)
        activation = sigmoid(z)
        activations.append(activation)

    # step 2
    # self.cost 作为构造时的一个参数，默认为CrossEntropyCost
    # 这里再次体现了我在本文开始说的，不同代价函数唯一的不同在于计算最后一层的$\delta^\ell$
    delta = (self.cost).delta(zs[-1], activations[-1], y)
    nabla_b[-1] = delta
    nabla_w[-1] = np.dot(delta, activations[-2].transpose())

    # step 3
    for l in range(2, self.num_layers):
        z = zs[-l]
        sp = sigmoid_prime(z)
        delta = np.dot(self.weights[-l+1].transpose(), delta)*sp
        nabla_b[-l] = delta
        nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()]
    return nabla_b, nabla_w