因子图/位姿图/后端优化

1. svo2 框架简略图

This content is only supported in a Docs.

2. 位姿图优化

2.1 位姿Pose Graph 的意义：只关心所有的相机位姿，省去了大量的特征点优化的计算，只保留了关键帧的轨迹，从而构建了所谓的位姿图，如图 1 所示。

图 1 Pose Graph 示意图。当我们不再优化 Bundle Adjustment 中的路标点，仅把它们看成对姿态节点的约束时，就得到了一个计算规模减小很多的 Pose Graph。
假设位姿图节点以$${\xi }_1,{\xi }_2,......,{\xi }_n$$表示相机位姿,对应的李群为$T_1,T_2,......,T_n$，边则是两个位姿节点之间相对运动的估计，来自于特征点法。则在位姿$T_i$与$T_j$间的变换可表示为：
$$\Delta T_{ij}=T_i^{-1}{T}_j（1）$$
实际当中该等式不会精确地成立，存在误差，因此可设立最小二乘误差，然后和通常的BA一样，讨论误差关于优化变量的导数。这里，我们把上式的姿态变化$\Delta T_{ij}$移至等式右侧，构建误差$ e_{ij}$ 可得：
$$e_{ij}=ln(\Delta T_{ij}^{-1}{T}_i^{-1}{T}_j{)}^{\vee }=ln(exp((-{\xi }_{ij}{)}^{\wedge })exp((-{\xi }_i{)}^{\wedge })exp((-{\xi }_j^{\wedge }){)}^{\vee }（2）$$
分别对i,j位姿增加左扰动$\delta {\xi }_i$与$\delta {\xi }_j$,则误差为：
$$\widehat{e_{ij}}=ln(T_{ij}^{-1}{T}_i^{-1}(exp((-\delta {\xi }_i{)}^{\wedge })exp(\delta {\xi }_j^{\wedge }))T_j{)}^{\vee }（3）$$
基于BCH近似与伴随矩阵性质可得：
$$\widehat{e_{ij}}=ln(T_{ij}^{-1}{T}_i^{-1}(exp((-\delta {\xi }_i{)}^{\wedge })exp(\delta {\xi }_j^{\wedge }))T_j{)}^{\vee }$$
$$=ln(T_{ij}^{-1}{T}_i^{-1}{T}_j(exp((-Ad(T_j^{-1})\delta {\xi }_i{)}^{\wedge })exp(Ad(T_j^{-1})\delta {\xi }_j^{\wedge })){)}^{\vee }$$
$$\approx ln(T_{ij}^{-1}{T}_i^{-1}{T}_j[I-(Ad(T_j^{-1})\delta {\xi }_i{)}^{\wedge }+(Ad(T_j^{-1})\delta {\xi }_j{)}^{\wedge }]{)}^{\vee }$$
$$\approx e_{ij}+\frac{\partial e_{ij}}{\partial \delta {\xi }_j}\delta {\xi }_j+\frac{\partial e_{ij}}{\partial \delta {\xi }_i}\delta {\xi }_i（4）$$
针对位姿变量由泰勒展开可得：
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_j}\delta {\xi }_j=-J_r^{-1}(e_{ij}).Ad(T_j)（5）$$
$$\frac{\partial e_{ij}}{\partial \delta {\xi }_i}\delta {\xi }_i=J_r^{-1}(e_{ij}).Ad(T_j)$$
取近似,如果误差接近于零，我们就可以设它们近似为 I 或:
$$J_r^{-1}(e_{ij})\approx I+\frac{1}{2}\left[\begin{array}{cc}{\Phi }^{\wedge }& {\rho }^{\wedge }\\ 0& {\Phi }^{\wedge }\end{array}\right]（6）$$
理论上来说，优化之后，由于每条边给定的观测数据并不一致，误差通常也不一定近似于零，所以简单地把这里的$$J_r$$ 设置为 I 会有一定的损失。所有的位姿顶点和位姿——位姿边构成了一个图优化，本质上是一个最小二乘问题，优化变量为各个顶点的位姿，边来自于位姿观测约束。记 E 为所有边的集合，那么总体目标函数为：
$$mi{n}_{\xi }=\frac{1}{2}\sum _{i,j\in ϵ}{e}_{ij}^T{\Sigma }_{ij}^{-1}{e}_{ij}（7）$$
最后再总结下：
第一，先由两个位姿顶点Ti和Tj、一个位姿变换边Tij构成一个优化函数，第二，扰动该函数并对两个位姿顶点的扰动量求偏导，得到J，然后计算H，第三，根据H△x=g得到扰动量△x，并对原先俩位姿进行更新，实现优化。（这点总结比较重要，不想清楚的话很容易在繁琐的推导中迷失掉，因此这里我们又有了一个新的认识，“前端”关注的是光度误差与重投影误差之类的东西，而这里“后端”关注的是已经知道了不同的位姿T，如何整体对它进行调整，这也就更符合了“后端”的含义） 把所有的顶点和边都考虑进来，总的目标函数就是：
$$mi{n}_{\xi }=\frac{1}{2}\sum _{i,j\in ϵ}{e}_{ij}^T{\Sigma }_{ij}^{-1}{e}_{ij}（7）$$

3. 因子图优化

3.1基础模型

设$C_i$表示关键帧 i 处的图片测量。在i时刻，相机可以观测多个路标 l,$C_i$包含多视图的测量$z_{il}$,其中$l\in C_i$表示时刻i观测到的l路标。则时刻i到时刻j所有的测量满足：
Z k ≐ { C i , I i j } ( i , j ) ∈ K k （ 8 ） Z_k \doteq \{C_i,I_{ij} \}_{(i,j)\in{K_k}} （8） Zk​≐{Ci​,Iij​}(i,j)∈Kk​​（8）
给定可得到的视觉和惯性测量$Z_k$和先验$p(X_0)$ ，变量 $X_k$的后验概率对应的因子图上的最大后验估计为（或者等价地，负对数的最小值。在零均值高斯噪声的假设下，负对数可以被写为残差平方和）:
$${\chi }_k^{\ast }=argmi{n}_{{\chi }_k}-lo{g}_{e}p({\chi }_k|Z_k)$$
$$=argmi{n}_{X_k}||r_0|{|}_{{\Sigma }_{ij}}^2+\sum _{(i,j)\in K_k}||r_{I_{ij}}|{|}_{{\Sigma }_{ij}}^2+\sum _{i\in K_k}\sum _{l\in C_i}||r_{C_{il}}|{|}_{{\Sigma }_C}^2（9）$$
其中r表示与测量相关的残差，$\Sigma$表示对应的协方差矩阵。通常残差是在给定状态和先验的前提下，量化测量值和预测值的差。实际应用中，采用无结构化方法。估计问题的输入是来自相机和IMU的测量。

3.2 概念引入

Kaess 等人提出的 iSAM（inremental Smooth and Mapping）中，对因子图进行更加精细的处理，使得它可以增量式地处理后端优化。为了进一步加速了计算，增量平滑算法的应用和视觉测量的无结构模型的使用成为可能，避免了对 3D 点的优化，具体模型示意图如下图所示。

图 2 左：VIO 中的视觉和惯性测量。 右图：因子图，其中几个 IMU 测量值汇总在单个预集成 IMU 因子中，无结构视觉因子约束关键帧观察相同的地标。
基于公式（9），视觉测量特征点相关的部分可以转换成
$$\sum _{i\in K_k}\sum _{l\in C_i}||r_{C_{il}}|{|}_{{\Sigma }_C}^2=\sum _{l=1}^L\sum _{i\in X(l)}||r_{C_{il}}|{|}_{{\Sigma }_C}^2(10)$$
在等式右侧，重写了每个路标 $l=1,.....L$表示路标集合。$x(l)$表示关键帧集l的集合，对于单图片测量 $z_{il}$表示残差标准建模是重投影误差如下（11）
$$r_{C_{il}}=z_{il}-\pi (R_i,p_i,{\rho }_l)(11)$$
其中，${\rho }_l\in {\mathbb{R}}^3$表示第 l个路标的位置,$\pi (.)$是标准的视角投影，其也编码了IMU-相机变换 $T_{BC}$.直接使用需要在优化中包含路标位置，类似与全局BA。为了避免优化路标，SVO2采用如上图2所示的一种称为无结构化方法，在避免优化路标的同时，因此保证了恢复MAP估计。

3.3 如何实现

具体做法如下第一：每次GN迭代，我们使用retractionSE（3）lift代价函数。对于视觉因子，这意味着原始残差(10)变成如下
$$\sum _{l=1}^L\sum _{i\in X(l)}||z_{il}-\pi (\delta {\varphi }_i,\delta p_i,\delta {\rho }_l)|{|}_{{\Sigma }_C}^2（12）$$
其中${\varphi }_i,\delta p_i,\delta {\rho }_l$是欧式修正,$\pi (.)$$是lifted代价函数。GN中的“solve”步骤基于残差的线性化为$${\sum }_{l=1}^L{\sum }_{i\in X(l)}||F_{il}\delta T_i+E_{il}\delta {\rho }_l-b_{il}|{|}^2（13）$$
其中，$$\delta T_i\doteq [\delta {\varphi }_i,\delta p_i{]}^T$$雅克比 $F_{il} , E_{il} $和向量 $b_{il}$（同时通过${\Sigma }_c^{1/2}$归一化）来线性化。向量 $b_{il}$是在线性化点的残差。
将(13)中的第二个求和写为矩阵形式，得到
$$\sum _{l=1}^L||F_l\delta T_{\chi (l)}+E_l\delta {\rho }_l-b_l|{|}^2（14）$$
其中$F_{l} , E_{l},b_l $为所有的$i \in \chi(l)$为堆叠得到。因为一个路标 l 出现在和(14)中的单独一项中，对于任何位姿扰动 $\delta T_{ \chi (l)} $，最小化代价函数 $$||F_l\delta T_{\chi (l)}+E_l\delta {\rho }_l-b_l|{|}^2$$的路标扰动 $\delta \rho_l $为
$$\delta {\rho }_l=-(E_l^T{E}_l{)}^{-1}{E}_l^T(F_l\delta T_{\chi (l)}-b_l)（15）$$
将(15)代入(14)，我们可以从优化问题中排除扰动 $\delta \rho_l $变量得：
$$\sum _{l=1}^L||(I-(E_l^T{E}_l{)}^{-1}{E}_l^T)(F_l\delta T_{\chi (l)}-b_l)|{|}^2（16）$$
其中，$I-(E_l^T{E}_l{)}^{-1}{E}_l^T$是$E_l$的正交投影。在附录IX-D中，我们展示了代价(55)可以被进一步变化，导致了一种更高效的应用。
该方法在BA文献中被广泛称为舒尔补技巧，其中一个标准的应用是更新 $\delta {\rho }_l$的线性化点通过back substitution[61]。反之，我们使用一个快速的线性三角化从位姿的线性化点中获得更新的路标位置。使用该方法，我们化简包含位姿和路标的一大组因子(10)为一组只包含位姿的更小的L个因子(16)。特别地，对应路标l 的因子仅包含观测到的状态 ，创建了如图2的连接关系。相同的方法被使用在MSC-KF[5]中来避免状态向量中包含路标。但是，由于MSC-KF仅能线性化和吸收一次测量，测量的处理需要被延迟直到相同路标的全部测量都被观测到为止。这不会发生在提出的基于优化的方法中，其允许多次线性化和新测量的增量添加。

20220329课件

4 . 位姿图

4.1 Pose Graph 的意义

带有相机位姿和空间点的图优化称为 BA，能够有效地求解大规模的定位与建图问题。但是，随着时间的流逝，机器人的运动轨迹将越来越长，地图规模也将不断增长。像 BA这样的方法，计算效率就会不断下降。根据前面的讨论，我们发现特征点在优化问题中占据了绝大多数部分。而实际上，经过若干次观测之后，那些收敛的特征点，空间位置估计就会收敛至一个值保持不动，而发散的外点则通常看不到了。对收敛点再进行优化，似乎是有些费力不讨好的。因此，我们更倾向于在优化几次之后就把特征点固定住，只把它们看作位姿估计的约束，而不再实际地优化它们的位置估计。沿着这个思路往下走，我们会发现：是否能够完全不管路标，而只管轨迹呢？
我们完全可以构建一个只有轨迹的图优化，而位姿节点之间的边，可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。
不同的是，一旦初始估计完成，我们就不再优化那些路标点的位置，而只关心所有的相机位姿之间的联系了。通过这种方式，我们省去了大量的特征点优化的计算，只保留了关键帧的轨迹，从而构建了所谓的位姿图（Pose Graph），如图 1 所示。

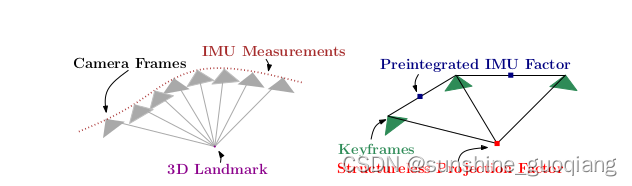
图 1 Pose Graph 示意图。当我们不再优化 Bundle Adjustment 中的路标点，仅把它们看成对姿态节点的约束时，就得到了一个计算规模减小很多的 Pose Graph。

我们知道在 BA 中，特征点数量远大于位姿节点的数量。一个关键帧往往关联了数百个关键点，而实时 BA 的最大计算规模，即使利用稀疏性，在当前的主流 CPU 上一般也就是几万个点左右。这就限制了SLAM 应用场景。所以，当机器人在更长的时间和空间中运动时，必须考虑一些解决方式：要么像滑动窗口法那样，丢弃一些历史数据 [77]；要么像Pose Graph 的做法那样，舍弃对路标点的优化，只保留 Pose 之间的边，使用 Pose Graph.

4.2 Pose Graph 的优化

4.3 因子图

1 如果需要最高精度，我们使用 iSAM2 （svopro[9]） 来联合优化整个轨迹的结构和运动。 iSAM2 是一种增量平滑算法，它利用因子图 [8] 的表达性来保持稀疏性，并仅识别和更新受新测量影响的通常较小的变量子集。
2. 在里程计设置中，这允许 iSAM2 实现与整个轨迹的批量估计相同的精度，同时保持实时能力。 使用 iSAM2 进行捆绑调整是一致的 [45]，这意味着估计的估计协方差与估计误差相匹配（例如，没有过度自信）。
3. 一致性是与附加传感器进行最佳融合的先决条件。 因此，在 [45] 中，我们展示了如何将 SVO 与惯性测量融合。 另一方面，LSD-SLAM 仅优化姿势图，并在计算后保持结构固定（达到一定比例）。 优化不捕获半密集深度估计和相机姿态估计之间的相关性。 这种深度估计和姿态优化的分离只有在每一步都产生最优解的情况下才是最优的。
4. 讨论生成测量模型以及旋转噪声的性质，推导出最大后验状态估计器的表达式。 我们的理论发展能够计算所有必要的雅可比矩阵，以分析形式的优化和后验偏差校正。 第二个贡献是表明预集成的 IMU 模型可以在因子图的统一框架下无缝集成到视觉惯性管道中。 这使得增量平滑算法的应用和视觉测量的无结构模型的使用成为可能，避免了对 3D 点的优化，进一步加速了计算。
5. SVO 的输出是选择的关键帧，其特征轨迹对应于三角地标。 该数据被传递到后端，该后端计算方程式中的视觉惯性 MAP 估计。 (25) (26) 使用 iSAM2 [3]。

由于测量 Z_k 是已知的，我们可以自由地将它们作为变量消除，并将它们视为实际未知数的联合概率因子的参数。
这自然会导致众所周知的因子图表示，这是一类可用于表示此类因子密度的二分图模型。图 1 给出了 VIO 问题的因子图的连通性示意图。因子图由未知数节点和定义在其上的概率因子节点组成，图结构表示每个因子涉及哪些未知数。该方法的关键特征是地标的线性消除。在每次 Gauss-Newton 迭代中都会重复消除，因此我们仍然可以保证获得最佳 MAP 估计。

图 1 左：VIO 中的视觉和惯性测量。 右图：因子图，其中几个 IMU 测量值汇总在单个预集成 IMU 因子中，无结构视觉因子约束关键帧观察相同的地标。

5 参考

SLAM14讲学习笔记
SLAM14讲学习笔记（七）后端（BA与图优化，Pose Graph优化的理论与公式详解、因子图优化）