坐标系的变换（Eigen库四元数表示的坐标）

最新推荐文章于 2025-04-15 21:12:53 发布

火星机器人life

最新推荐文章于 2025-04-15 21:12:53 发布

阅读量1.1w

点赞数 2

分类专栏： SLAM 文章标签： slam 四元数坐标变换

本文链接：https://blog.csdn.net/ktigerhero3/article/details/86244211

版权

SLAM 专栏收录该内容

47 篇文章

订阅专栏

本文详述了如何利用Eigen库中的四元数进行空间坐标转换，包括从一个坐标系到另一个坐标系的旋转和平移计算，以及逆向求解的过程。通过具体示例，演示了四元数在机器人定位和姿态估计中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文主要介绍使用Eigen库中的四元数进行空间坐标的转换。
Eigen库的结构体对应的名称如下：
旋转矩阵（3×3） Eigen::Matrix3d
旋转向量（3×1）Eigen::AngleAxisd
欧式变换矩阵（4×4） Eigen::Isometry3d
四元数（4×1）Eigen::Quaterniond

坐标系转换如图
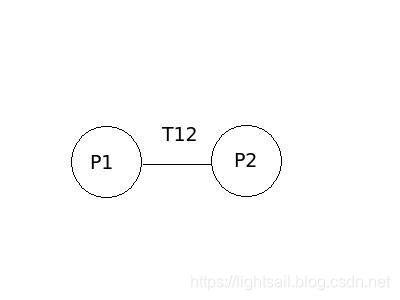
在这里插入图片描述

假设机器在p1处在世界坐标系下的位姿为（x，y，z，roll,pitch,yaw）=（1，1，0，0,0,0,），p2处世界坐标系下的位姿（x，y，z，roll,pitch,yaw）=（2，2，0，0 ，0，45）

1.已知p1,p2求p1 和p2之间的转换T12

此例中T12结果简单表示为(1,1,0,0,0,45)
程序如下：

#include<iostream>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>
int main()
{
    //1.p1 world position
    double p1yaw=0;
    double p1x=1;
    double p1y=1;
    Eigen::AngleAxisd rotzp1(p1yaw*M_PI/180, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d  t1= Eigen::Vector3d(p1x,p1y, 0);
    Eigen::Quaterniond q1=Eigen::Quaterniond(rotzp1);
    //cout<<"q1.vec()"<<q1.vec()<<endl;
    cout<<"p1 eular angle in world axis"<<(180/M_PI)*q1.matrix().eulerAngles(0,1,2)<<endl;
    cout<<"p1 position in world axis"<<t1<<endl;
   //2.p2 world position
    double p2yaw=45;
    double p2x=2;
    double p2y=2;
    Eigen::AngleAxisd rotzp2(p2yaw*M_PI/180, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d  t2= Eigen::Vector3d(p2x,p2y, 0);
    Eigen::Quaterniond q2=Eigen::Quaterniond(rotzp2);
    //cout<<"q1.vec()"<<q1.vec()<<endl;
    cout<<"p2 eular angle in world axis"<<(180/M_PI)*q2.matrix().eulerAngles(0,1,2)<<endl;
    cout<<"p2 position in world axis"<<t2<<endl;


    // 3.calculate T12
    //q1*q12=q2
    Eigen::Quaterniond q12=q1.inverse()*q2;
    cout<<"rotaion from p1  to p2 "<<(180/M_PI)*q12.matrix().eulerAngles(0,1,2)<<endl;

   // Eigen::Vector3d t2=t1+q1.toRotationMatrix()*t12;

    Eigen::Vector3d  t12=q1.toRotationMatrix().inverse()*(t2-t1);
    cout<<"translation base on p1 aixs t12="<<t12<<endl;
}

2已知p1和t12求p2

假设机器在p1处在世界坐标系下的位姿为（x，y，z，roll,pitch,yaw）=（1，1，0，0,0,0,），p1 和p2之间的转换（p1经过旋转和平移）为t12表示为(1,1,0,0,0,45)，
求p2处世界坐标系下的位姿（x，y，z，roll,pitch,yaw）？
结果为（2，2，0，0,0,45）
程序如下：

#include<iostream>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>

using namespace std;
int main()
{
//    //1.p1 world position
    double p1yaw=0;
    double p1x=1;
    double p1y=1;
    Eigen::AngleAxisd rotzp1(p1yaw*M_PI/180, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d  t1= Eigen::Vector3d(p1x,p1y, 0);
    Eigen::Quaterniond q1=Eigen::Quaterniond(rotzp1);
    //cout<<"q1.vec()"<<q1.vec()<<endl;
    cout<<"p1 eular angle"<<(180/M_PI)*q1.matrix().eulerAngles(0,1,2)<<endl;
    
    //2. t12 value
    double t12yaw=45;
    double t12x=1;
    double t12y=1;
    Eigen::AngleAxisd rott12(t12yaw*M_PI/180, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d  t12= Eigen::Vector3d(t12x,t12y, 0);
    Eigen::Quaterniond q12=Eigen::Quaterniond(rott12);
     cout<<"t12 rotation eular angle "<<(180/M_PI)*q12.matrix().eulerAngles(0,1,2)<<endl;
  //  cout<<"q12.vec()"<<q12.vec()<<endl;
     
//    3.calculate p2 world positon
    Eigen::Quaterniond q2=q1*q12;
   // cout<<" q2 vector " <<q2.vec()<<endl;
    Eigen::Vector3d t2=t1+q1.toRotationMatrix()*t12;
    cout<<"t2="<<t2<<endl;
    cout<<"t2 eular angle "<<(180/M_PI)*q2.matrix().eulerAngles(0,1,2)<<endl;
}

参考文献
Eigen中四元数、欧拉角、旋转矩阵、旋转向量之间的转换
https://blog.csdn.net/yang__jing/article/details/82316093