从二分逼近领略计算科学的魅力

计算分两种：
数学家们的方法（倾向于给出解析解），
计算机科学家的方法（设计算法，重复的操作交给CPU）

还有一点值得说明的是：
比如 $1+2+\cdots +100$ 的计算，高斯（等差数列的方法 $(S_n+S_n)/2$，一个前 $n$ 项和为顺序，$S_n = 1+2+\cdots+100$，第二个为逆序，$S_n=100+99+\cdots+1$）之后，几乎每一个小孩都知道该怎么做，然而呢，我认为，这并（找规律）非计算机的做法，计算机的做法自然是简单的循环遍历相加。类似的例子见三个瓶盖能换一瓶水，问100个人需要喝水，最少需要买多少瓶水即可解决100人的喝水问题（这篇文章提供了两种思路，一种是找规律型的，这是人的智慧或者思考问题的方式，一种是计算机的工作方式）。

比如针对实数域上的函数 $f(x)$，如果存在实数 $x_0$ 使得 $f(x_0)=0$，则 $x=x_0$ 是函数 $f(x)$的零点。如果函数 $f(x)$是连续函数，且在区间 $[x_1,x_2]$上是单调函数，只要 $f(x_1)f(x_2)<0$，就说明在区间 $[a, b]$ 内一定有零点，此时就可使用二分逼近法近似地找到这个零点。这种情况下，可按如下流程实施二分逼近法：

• $m=\frac{x_1+x_2}2$

• $f(x_1)f(m)<0\quad\Rightarrow\quad x_2=m$

• $f(x_1)f(m)>0\quad \Rightarrow\quad x_1=m$

• $(x_2-x_1)<\epsilon \;?$

从上述过程可以看到，每次运算之后，区间范围缩小一半，呈现线性收敛速度。设方程为 $f(x)=2x^2+3.2x-1.8$，求根精度为 $\epsilon=10^{-9}$，在$[-0.8,0.8]$寻找其根；

typedef double (*FuncPtr) (double);
const double Epsilon = 1e-9;

double dichotomyApprox(double x1, double x2, FuncPtr f)
{
    assert(f(x1)*f(x2)<0.0);
    double m = (x1+x2)/2;
    while ((x2-x1)>Epsilon)
    {
        f(x1)*f(m)<0. ? x2 = m : x1 = m;
        m = (x1+x2)/2;
    }
    return m;
}

既然以精度（precision）设限，其实迭代次数是与解的位置无关的，而与精度直接相关，本例精度 $\epsilon=10^{-9}$，采用二分法的形式 $2^{29}<10^9<2^{30}$，迭代次数应当在30次左右。

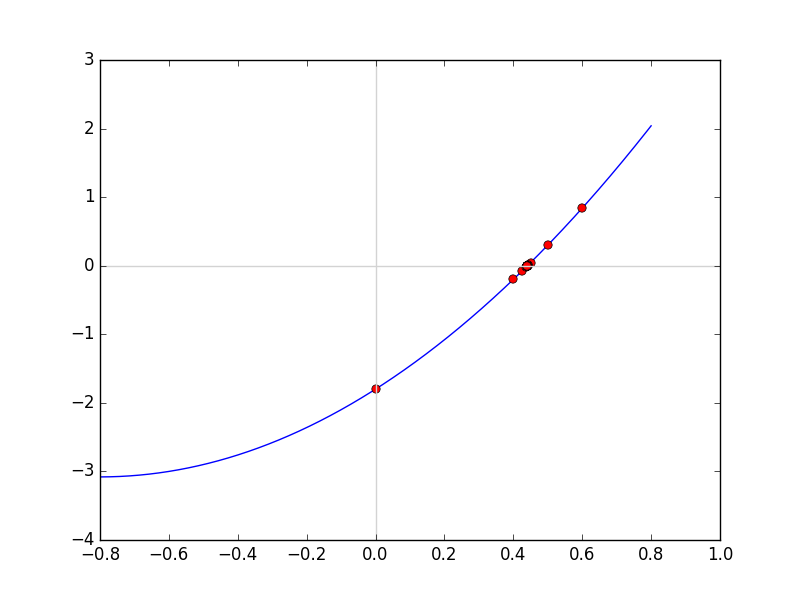
二分逼近求解实数的平方根的应用实例，请见 平方根的计算（二分逼近、牛顿拉普生法） 。