四旋翼数学模型——动力模型

---

一、动力模型

---

动力模型研究四旋翼机体系 $xyz$ 轴上的力矩与四个电机输入油门的关系。这个过程中，假设电池电压不变，那么油门（即PWM波占空比）越大，则电调输入的等效电压越大，电机与螺旋桨转速越快，产生的升力越大；每个螺旋桨通过升力与反扭力转化为力矩与反扭矩，在 $xyz$ 三个轴上合成新的力矩，以下做定量分析。

---

1.1 符号说明

变量	符号	单位
每个电机的油门	${\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4$	归一化 $[0,1]$
每个螺旋桨产生的升力	$F_1,F_2,F_3,F_4$	$\mathrm{N}$
每个螺旋桨产生的诱导阻力	$f_1,f_2,f_3,f_4$	$\mathrm{N}$
每个螺旋桨升力产生的力矩	$M_1,M_2,M_3,M_4$	$\mathrm{N}\cdot \mathrm{m}$
每个螺旋桨产生的反扭矩	$M_{r1},M_{r3},M_{r3},M_{r4}$	$\mathrm{N}\cdot \mathrm{m}$
$xyz$ 轴上的合力矩	${\tau }_x,{\tau }_y,{\tau }_z$	$\mathrm{N}\cdot \mathrm{m}$
合升力	$T$	$\mathrm{N}$

注：为简洁起见，以下省略 $1,2,3,4$ 下标。

常量	符号	取值	含义
电机时间常数	$T_m$	$260\mathrm{m}\mathrm{s}$	电机转速达到稳定转速63.2%所需时间
电机与四旋翼重心距离	$d$	$0.225\mathrm{m}$	450四旋翼，机臂长度一半 225mm
电机转速斜率	$C_m$	$706.1\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$	油门从增加1，电机转速增加量
电机转速截距	${\varpi }_m$	$170.47\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$	油门为0时，电机转速
升力系数	$c_T$	$1.201\times 10^{-5}\mathrm{N}/(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}{)}^2$	单个螺旋桨转速增加 $1\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$，升力增加大小
反扭矩矩系数	$c_M$	$1.574\times 10^{-7}\mathrm{N}\cdot \mathrm{m}/(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}{)}^2$	单个螺旋桨转速增加 $1\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$，扭矩增加大小

---

1.2 电机模型

1.2.1 原理

给电机的油门越大，电机与螺旋桨转速（以下简称电机转速）越快，油门与电机稳态转速之间接近线性关系。但是给电机一个油门之后，电机并不能立即达到对应的转速，可以把电机近似为一阶系统

$$T_m\frac{\mathrm{d}\varpi (t)}{\mathrm{d}t}+\varpi (t)=C_m\sigma (t)+{\varpi }_m\text{\hspace{1em}(1.1)}$$

其中，$C_m$为电机转速斜率，定义为油门从增加1，电机转速增加量；${\varpi }_m$ 为电机转速截距，定义为油门为0时，电机的转速；$C_m\sigma (t)+{\varpi }_m$ 代表电机的稳定转速，与油门线性相关。

为方便理解，式(1.1) 可转化为

$$\dot{\varpi }(t)=\frac{\mathrm{d}\varpi (t)}{\mathrm{d}t}=\frac{1}{T_m}(C_m\sigma (t)+{\varpi }_m-\varpi (t))$$

可见，随着电机转速 $\varpi (t)$ 的增加，电机转速增量 $\dot{\varpi }(t)$ 逐渐减小，电机转速逐渐达到给定转速。这个过程中，如果电机时间常数 $T_m$ 越大，则每次转速的增量越小，达到稳定转速的时间越长。

---

1.2.2 仿真

假设四个电机的输入油门分别时 $0.7,0.6,0.5,0.4$，观察 $2\mathrm{s}$ 内四个电机转速变化。

%% 模型测试
global dt Tm Cm varpim

dt = 1e-3;              % 仿真时间步长
Cm = 706.01;            % 油门增大1，电机转速变化(RPM)
varpim = 170.47;        % 零占空比时电机转速(RPM)
Tm = 0.260;             % 电机时间常数


N = 2000;
t = 0:dt:dt*(N-1);
sigma = [0.7; 0.6; 0.5; 0.4];
varpi = zeros(N, 4);

k=1;
for tt=0:dt:(N-2)*dt
    k = k+1;
    % 动力单元模型
    varpi(k, 1) = motor(sigma(1), varpi(k-1, 1));       % 电机1转速
    varpi(k, 2) = motor(sigma(2), varpi(k-1, 2));       % 电机2转速
    varpi(k, 3) = motor(sigma(3), varpi(k-1, 3));       % 电机3转速
    varpi(k, 4) = motor(sigma(4), varpi(k-1, 4));       % 电机4转速
end

figure(1);plot(t, varpi(:,1), 'LineWidth', 1.5); hold on
plot(t, varpi(:,2), 'LineWidth', 1.5);
plot(t, varpi(:,3), 'LineWidth', 1.5);
plot(t, varpi(:,4), 'LineWidth', 1.5); hold off

legend(['\sigma_1=' num2str(sigma(1))], ['\sigma_2=' num2str(sigma(2))],['\sigma_3=' num2str(sigma(3))],['\sigma_4=' num2str(sigma(4))]);
xlabel('时间 t (s)');ylabel('转速 \varpi  (rad/s)');title('电机模型测试'); grid on; grid minor

%% 电机模型
% 输入：油门大小 sigma（0-1）
%       电机上一时刻的转速（rad/s）
% 输出：此时刻电机转速（rad/s）

function varpi = motor(sigma, varpi_)
    global dt Tm Cm varpim;
    dvarpi = (Cm * sigma + varpim - varpi_) / Tm * dt;
    varpi = varpi_ + dvarpi;
end

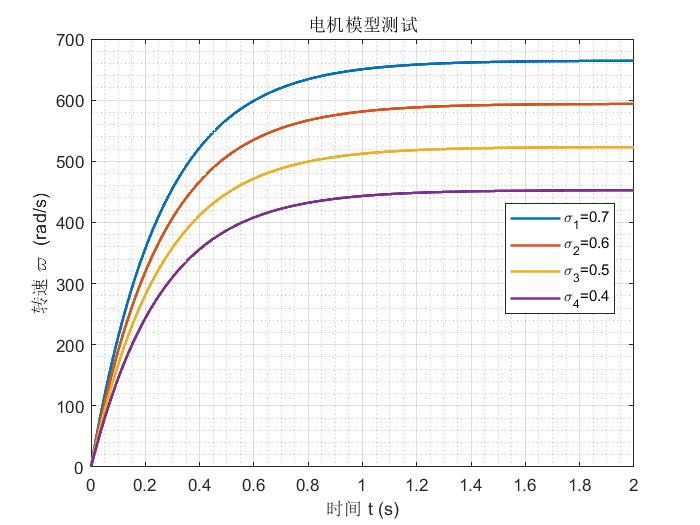
可见，油门越大，电机稳定转速越快，电机在 $260\mathrm{m}\mathrm{s}$ 达到稳定转速的63.2% 。

---

1.3 动力合成模型

1.3.1 合升力

螺旋桨转动产生升力，该升力和螺旋桨转速的平方成正比

$$f=c_T{\varpi }^2\text{\hspace{1em}(1.2)}$$

其中，$c_T$为升力系数。

四个螺旋桨产生的总升力大小为

$$T=c_T({\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2+{\varpi }_4^2)\text{\hspace{1em}(1.3)}$$

1.3.2 $x,y$ 轴力矩

螺旋桨产生的升力作用在四旋翼上，会导致机体转动，也即产生了力矩。力矩的定义为

$$M=d\times F\text{\hspace{1em}(1.4)}$$

其中，$d$ 为支点到力作用点的矢量，$F$ 为力矢量；$M$为力矩，单位 $\mathrm{N}\cdot \mathrm{m}$，其大小为 $|d|\cdot |F|\cdot \sin \theta$，方向服从右手法则垂直于 $d$ 与 $F$ 所在的平面。

如下图所示，$O$为四旋翼重心，$F_1$ 为1号螺旋桨产生的升力，垂直纸面向外，容易得出力矩

$$M_1=d\times F_1\text{\hspace{1em}(1.5)}$$

$M_1$ 在机体系 $x,y$ 轴上的分量分别为

$$M_{1x}=-\frac{\sqrt{2}}{2}d{F}_1=-\frac{\sqrt{2}}{2}d{c}_T{\varpi }_1^2\text{\hspace{1em}(1.6)}$$

$$M_{1y}=\frac{\sqrt{2}}{2}d{F}_1=\frac{\sqrt{2}}{2}d{c}_T{\varpi }_1^2\text{\hspace{1em}(1.7)}$$

规定：刚体绕轴转动，力矩为正，刚体绕轴逆时针转动，力矩为负，刚体绕轴为顺时针转动（将坐标系箭头朝向自己，判断顺逆时针）。

1号螺旋桨产生力矩在 $x$ 轴上分量为负，导致机体绕 $x$ 轴逆时针转动，也即滚转角减小；在 $y$ 轴上分量为正，机体系绕 $y$ 逆时针转动，俯仰角增大。事实上，1号螺旋桨拉力很大将导致机体右前方升高，即俯仰角增大，滚转角减小，因此上面的规定是合理的。

同理可得其他三个螺旋桨产生的力矩 $M_2,M_3,M_4$，通过力矩的矢量合成，易得 $x,y$ 方向的合力矩为

$${\tau }_x=\frac{\sqrt{2}}{2}d{c}_T(-{\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\text{\hspace{1em}(1.8)}$$

$${\tau }_y=\frac{\sqrt{2}}{2}d{c}_T({\varpi }_1^2+{\varpi }_2^2-{\varpi }_3^2-{\varpi }_4^2)\text{\hspace{1em}(1.9)}$$

1.3.3 $z$轴力矩

螺旋桨在转动的时候，迅速冲撞着螺旋桨平面内的空气。根据牛顿第三定律，空气也会给螺旋桨一个反方向的阻力。如下图所示，俯视逆时针转动的1号螺旋桨，螺旋桨转动方向为 $v$，将受到空气的阻力 $f_1$，产生力矩 $M_{r1}$

$$M_{r1}=r\times f_1\text{\hspace{1em}(1.10)}$$

其中，螺旋桨各点所受空气阻力并不相等，$f_1$ 为等效空气阻力，$r$ 为螺旋桨长度的一半。

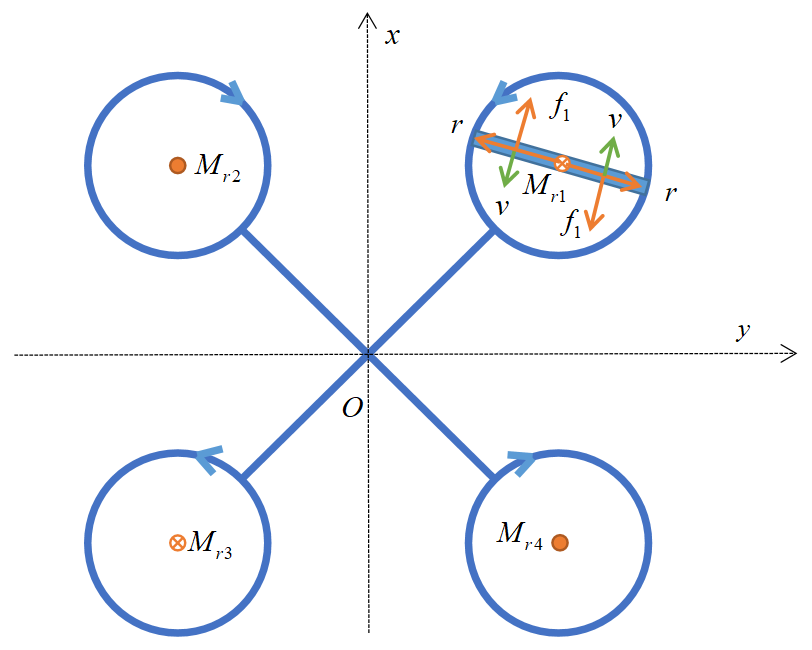
由于该力矩使得无人机转动，是反作用力效果，故称该力矩为反扭矩，该空气阻力称为反扭力。根据右手螺旋定则容易得出，叉乘后的方向垂直纸面向内，也即 $z$ 轴分量为正，这将导致四旋翼逆时针转动（注意将 $z$ 轴箭头朝向自己），俯视而看，四旋翼将顺时针转动。

同理，$M_{r3}$ 也将导致四旋翼顺时针转动（俯视），偏航角增大；而$M_{r2},M_{r4}$ 将导致四旋翼逆时针转动（俯视），偏航角减小。

以上说明反扭矩的来源及对四旋翼偏航角的影响，但根据式(1.10) 很难计算的反扭矩，因为平均的反扭力 $f_1$ 难以得出，因此，采用实验方式得出反扭矩。实验表明，反扭矩也和螺旋桨转速的平方成正比

$$M_r=c_M{\varpi }^2\text{\hspace{1em}(1.11)}$$

其中，$c_M$ 称为反扭矩系数，代表单个螺旋桨转速增加 $1\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$，反扭矩增加的大小。

因此，四个螺旋桨产生的反扭矩之和为

$${\tau }_z=c_M({\varpi }_1^2-{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\text{\hspace{1em}(1.12)}$$

1.3.4 模型小结与仿真

综上，得到完整的动力合成模型如下

$$\begin{array}{rl}& T=c_T({\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2+{\varpi }_4^2)\\ & {\tau }_x=\frac{\sqrt{2}}{2}d{c}_T(-{\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\\ & {\tau }_y=\frac{\sqrt{2}}{2}d{c}_T({\varpi }_1^2+{\varpi }_2^2-{\varpi }_3^2-{\varpi }_4^2)\\ & {\tau }_z=c_M({\varpi }_1^2-{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\end{array}$$

假设四个电机的输入油门分别时 $0.7,0.6,0.5,0.4$，计算 $2\mathrm{s}$ 内四个螺旋桨产生的合升力及力矩大小。

%% 模型测试
global dt Tm Cm varpim d cT cM

dt = 1e-3;              % 仿真时间步长
Cm = 706.01;            % 油门增大1，电机转速变化(RPM)
varpim = 170.47;        % 零占空比时电机转速(RPM)
Tm = 0.260;             % 电机时间常数
d = 0.225;              % 450mm/2
cT = 1.201e-5;          % 升力系数
cM = 1.574e-7;          % 反扭力系数

N = 2000;
t = 0:dt:dt*(N-1);
sigma = [0.7; 0.6; 0.5; 0.4];
varpi = zeros(N, 4);
T = zeros(N, 1);
tau = zeros(N, 3);

k=1;
for tt=0:dt:(N-2)*dt
    k = k+1;
    % 电机模型
    varpi(k, 1) = motor(sigma(1), varpi(k-1, 1));       % 电机1转速
    varpi(k, 2) = motor(sigma(2), varpi(k-1, 2));       % 电机2转速
    varpi(k, 3) = motor(sigma(3), varpi(k-1, 3));       % 电机3转速
    varpi(k, 4) = motor(sigma(4), varpi(k-1, 4));       % 电机4转速
    
    [T(k), tau(k,:)] = power_mix(varpi(k, :));
end

figure(1);subplot(211); plot(t, T, 'linewidth', 1.5); title('动力合成模型');ylabel('升力 (N)');
subplot(212);plot(t, tau(:,1), 'linewidth', 1.5);hold on
plot(t, tau(:,2),'linewidth', 1.5);plot(t, tau(:,3),'linewidth', 1.5);hold off
ylabel('力矩 (N\cdotm)');xlabel('时间 (t)'); legend('\tau_x', '\tau_y', '\tau_z');

%% 电机模型
% 输入：油门大小 sigma（0-1）
%       电机上一时刻的转速（rad/s）
% 输出：此时刻电机转速（rad/s）

function varpi = motor(sigma, varpi_)
    global dt Tm Cm varpim;
    dvarpi = (Cm * sigma + varpim - varpi_) / Tm * dt;
    varpi = varpi_ + dvarpi;
end

%% 动力合成模型
% 输入：四个电机转速
% 输出：合升力与三轴力矩
function [T, tau] = power_mix(varpi)
    global cT cM d;
    T = cT * sum(varpi.^2);
    tau(1) = sqrt(2)/2 * d * cT * (-varpi(1)^2 + varpi(2)^2 + varpi(3)^2 - varpi(4)^2);
    tau(2) = sqrt(2)/2 * d * cT * ( varpi(1)^2 + varpi(2)^2 - varpi(3)^2 - varpi(4)^2);
    tau(3) = cM * (varpi(1)^2 - varpi(2)^2 + varpi(3)^2 - varpi(4)^2);
end

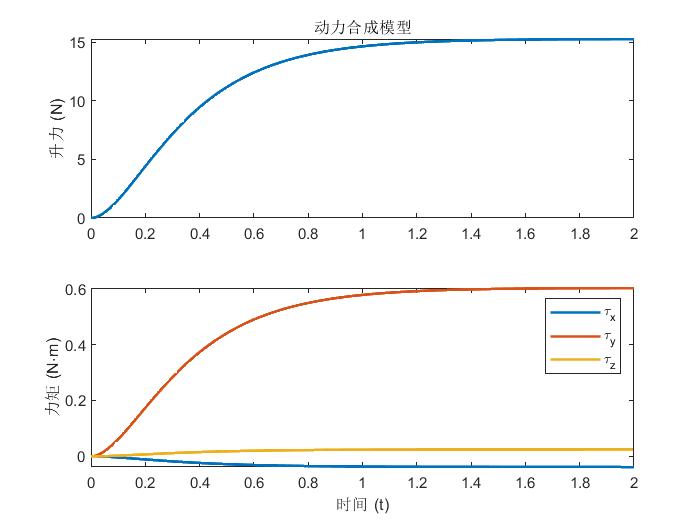
可见，产生了大约1.5kg 的拉力，一般450四旋翼空载质量也大约1.5kg，产生这样的拉力是合理的。绕 $y$ 轴的力矩很大，并且是正数，说明这会使得无人机绕 $y$ 逆时针运动，俯仰角增大。实际上，由于1号2号电机油门很大，相应的螺旋桨也会产生很大拉力，是的无人机俯仰角增大，与仿真结果一致。同理可分析绕 $x$ 轴力矩较小，且会让滚转角稍微变小。同时，由于反扭矩系数远小于升力系数，绕 $z$ 的力矩会比绕 $x,y$ 的力矩小一到两个数量级。这说明相比于改变四旋翼俯仰角或滚转角，改变无人机偏航角更为困难，需要电机油门变化量更大，在设计控制系统时应注意。

---

1.4 动力模型小结

动力模型假设了电池电压不变，建立了四旋翼机体系下升力与力矩 与 四个电机油门的关系。完整模型如下

$$\begin{array}{rl}& T_m{\dot{\varpi }}_1(t)+{\varpi }_1(t)=C_m{\sigma }_1(t)+{\varpi }_m\\ & T_m{\dot{\varpi }}_2(t)+{\varpi }_2(t)=C_m{\sigma }_2(t)+{\varpi }_m\\ & T_m{\dot{\varpi }}_3(t)+{\varpi }_3(t)=C_m{\sigma }_3(t)+{\varpi }_m\\ & T_m{\dot{\varpi }}_4(t)+{\varpi }_4(t)=C_m{\sigma }_4(t)+{\varpi }_m\\ & T=c_T({\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2+{\varpi }_4^2)\\ & {\tau }_x=\sqrt{2}/2d{c}_T(-{\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\\ & {\tau }_y=\sqrt{2}/2d{c}_T({\varpi }_1^2+{\varpi }_2^2-{\varpi }_3^2-{\varpi }_4^2)\\ & {\tau }_z=c_M({\varpi }_1^2-{\varpi }_2^2+{\varpi }_3^2-{\varpi }_4^2)\end{array}$$

专门针对四旋翼建模与控制出了一期教程哦，欢迎购买支持，课程链接 火力教育 四旋翼建模与控制