自动化电子结构哈密顿量：可投影的解纠缠函数

在周期晶体中，电子结构通常使用单粒子布洛赫波函数来描述。诚然，选择一个同为周期性的基组来描述这些波函数通常是有益的，但实空间中的局域轨道基矢也是一个不错的选择。

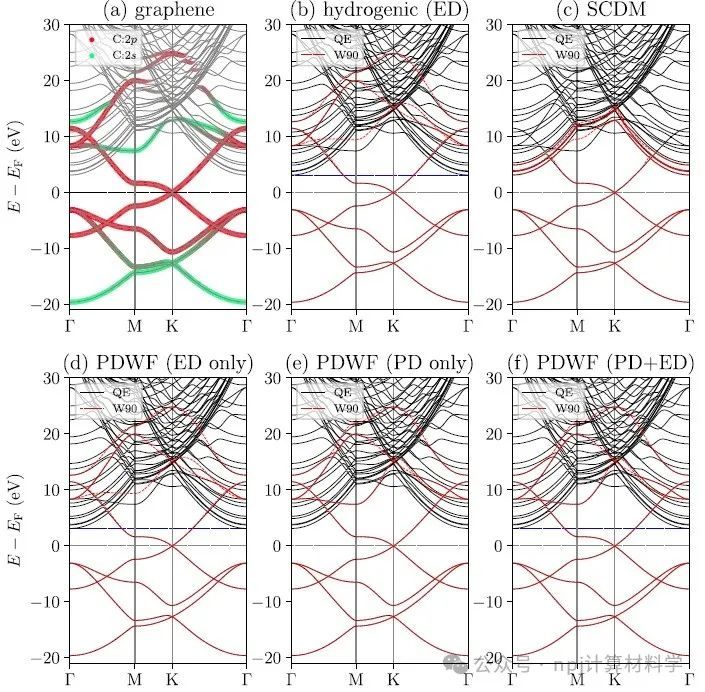
Fig. 1 Comparisons of graphene band structures interpolated using different methods.

Wannier函数（WFs）就是这样一种选择，它可以通过将周期波函数从倒空间变换到实空间来获得。通过优化规范选择以提供最局域化的WFs集合，可以获得最大程度局域化的Wannier函数（MLWFs）。局域化的波函数不仅有助于固体材料化学键的深入分析，还与现代电极化理论建立了形式联系。

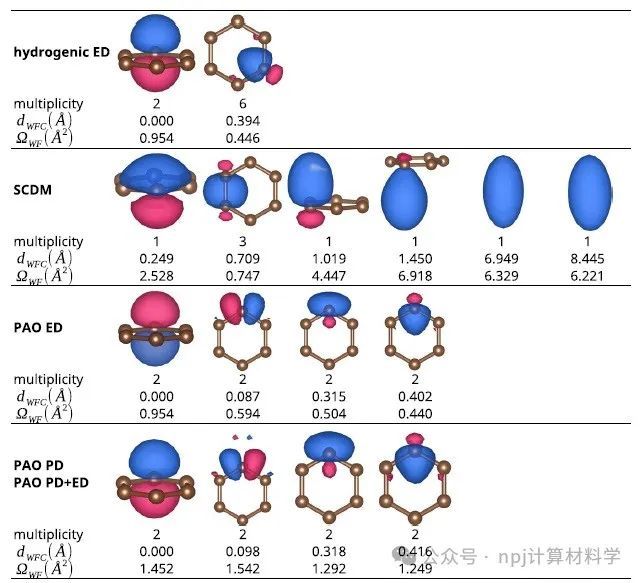
Fig. 2 Graphene MLWFs: shapes, centers, and spreads obtained using different methods.

此外，MLWFs的空间局域性有利于物理算符的插值计算，这使得需要密集布里渊区采样的材料性质计算（如费米面、轨道磁化、反常霍尔电导率和自旋霍尔电导率等）成为可能。

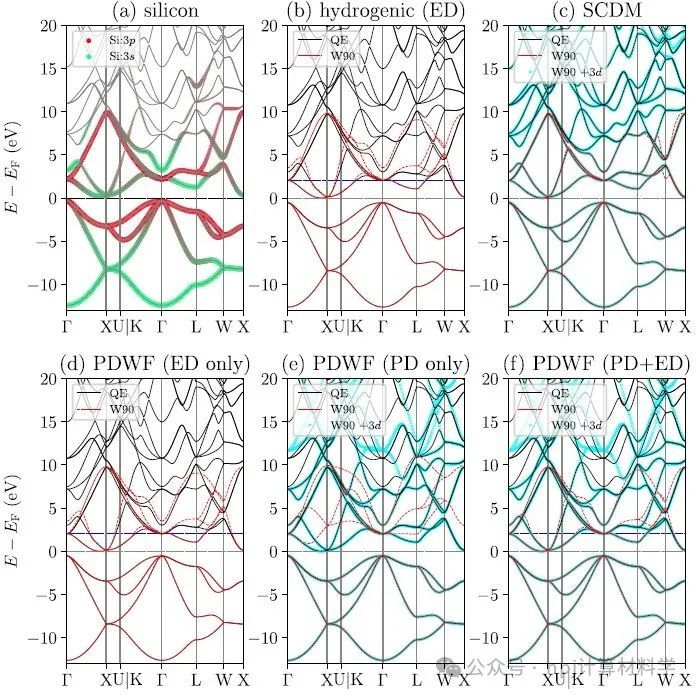
Fig. 3 Comparisons of silicon band structures interpolated using different methods.

然而，获得准确且紧凑的MLWFs通常需要化学直觉和反复测试，这即使对于经验丰富的研究人员来说也是一个挑战，这也是高通量计算的一个障碍。

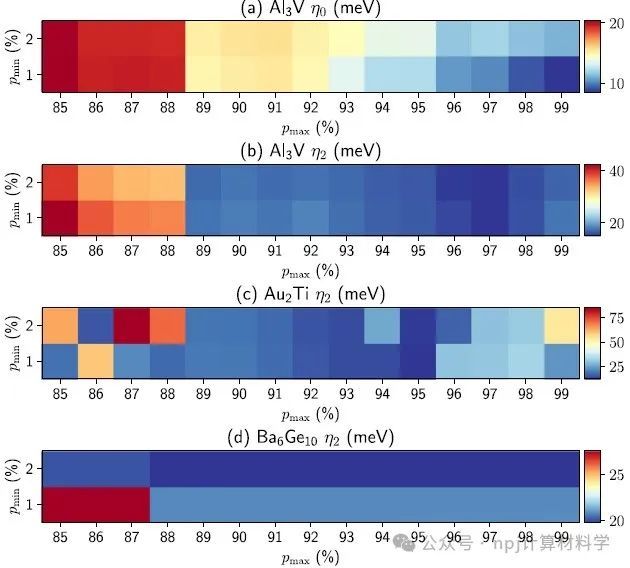
Fig. 4 Quality of band interpolations: band distances for different choices of pmin and pmax. 

来自瑞士洛桑联邦理工学院材料理论与模拟中心的Junfeng Qiao等，提出了一种基于MLWFs的方法，可以自动、稳健、可靠地构建紧束缚模型，即可投影的解纠缠Wannier函数（PDWFs）。

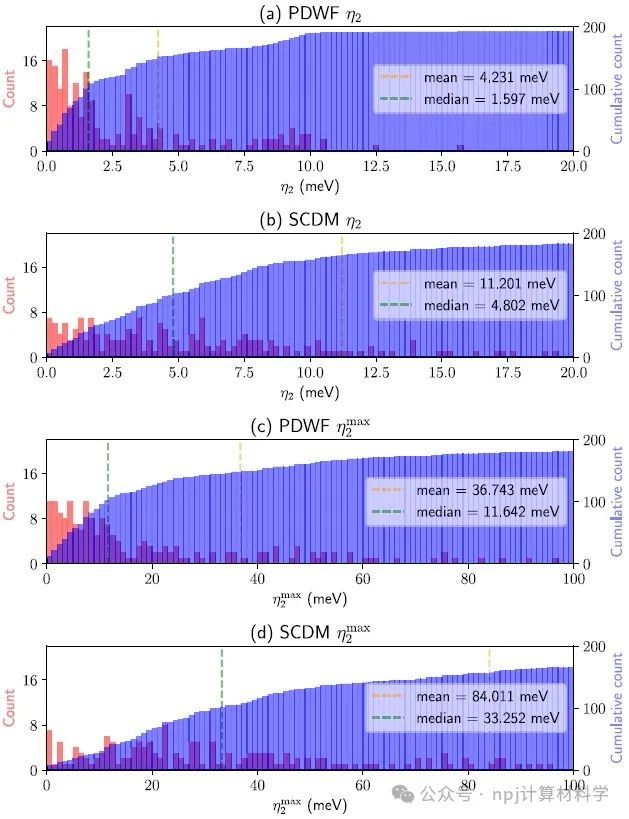
Fig. 5 Histogram (red) and cumulative histogram (blue) of the band distances η2 and ηmax 2 for 200 reference structures.

该方法首先选择基于物理灵感的轨道（赝势中的赝原子轨道，PAOs）为MLWFs的初始假设，再根据每个态在PAOs上的可投影性来决定对其的操作（丢弃、保留或是解纠缠）。

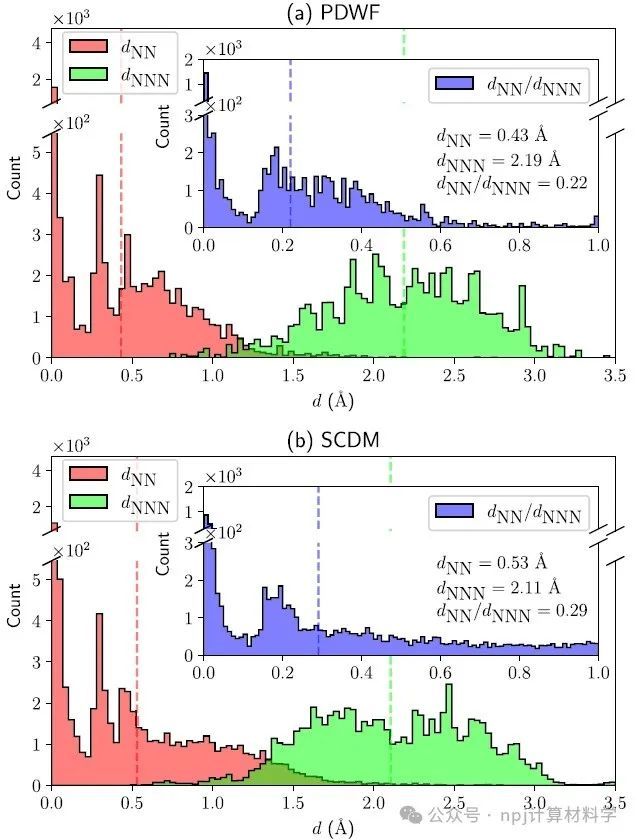
Fig. 6 Histogram of the distances of the WF centers from the NN atom (red, dNN) and NNN atom (green, dNNN), for 200 reference structures.

作者额外通过能量窗口增强了基于可投影性的选择，以确保围绕费米能级或导带边缘的所有状态都被准确再现，这表明此种组合即使在选择最小初始原子轨道集时也能实现准确的插值。

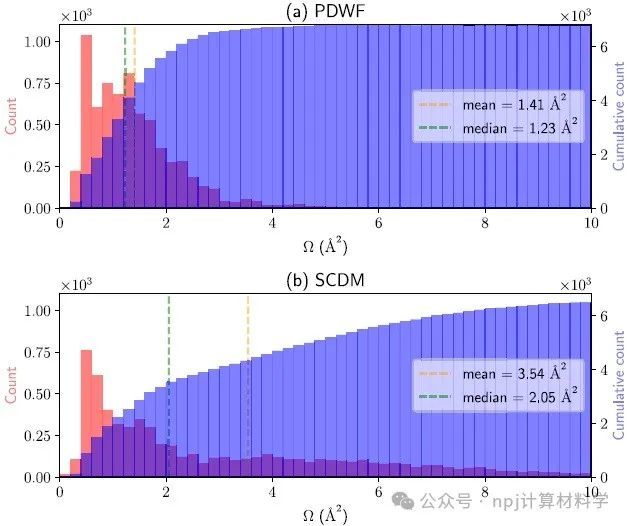
Fig. 7 Histogram (red) and cumulative histogram (blue) of WF spreads for 200 reference structures.

作者将新开发的PDWFs方法与一种同为完全自动化的方法（密度矩阵选列法，SCDM）进行了比较，通过对200个结构的详细研究，PDWFs得到了更准确的能带插值，且所得MLWFs比SCDM更局域化。

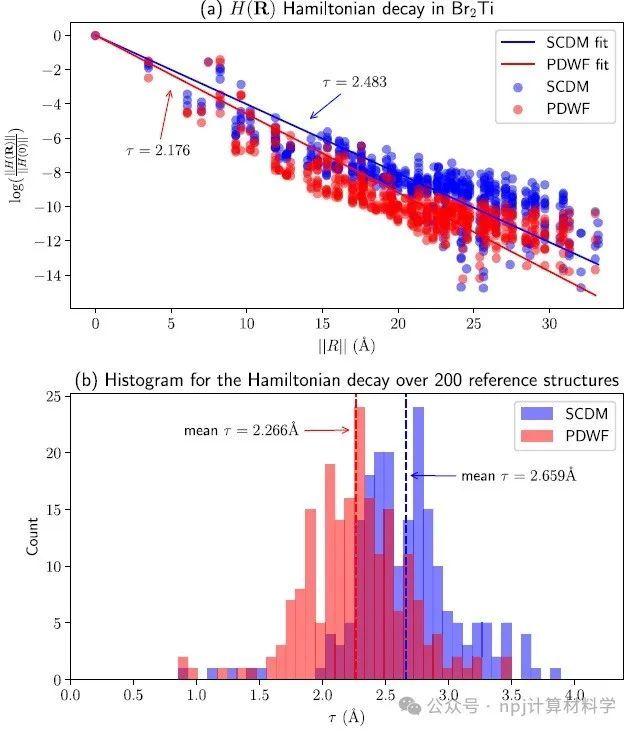
Fig. 8 Exponential decay of the Hamiltonian H(R) in the basis of MLWFs.

作者所提出的方法和工作流对新材料的高通量计算及相关物理性质的深入研究具有重要价值。该文近期发布于npj Computational Materials9: 208 (2023)。

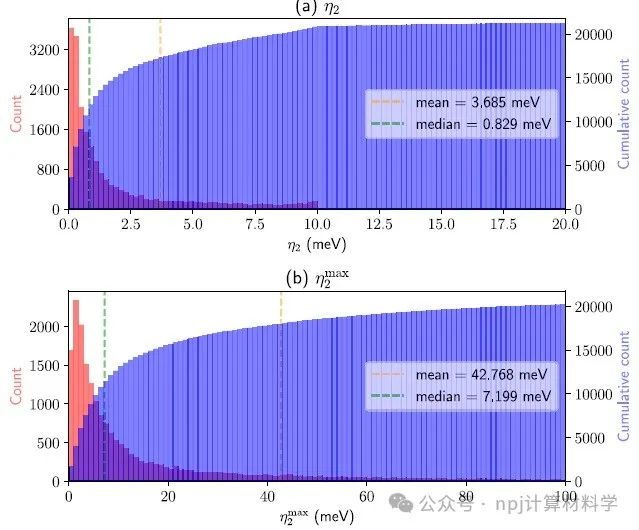
Fig. 9 Histogram (red) and cumulative histogram (blue) of the PDWF band distances for 21,737 non-magnetic structures obtained from the Materials Cloud MC3D database.

Editorial Summary

Automating Electronic Structure Hamiltonians: Projectability-Disentangled Wannier Functions

In periodic crystals, the electronic structure is usually described using one-particle Bloch wavefunctions. While choosing a basis set that is also periodic to describe these wavefunctions can often be beneficial, an alternative approach is to adopt localized orbitals in real space. 

One such choice of orbitals are Wannier functions (WFs), that can be obtained by Fourier transforming the periodic wavefunctions from reciprocal to real space. By a gauge choice that is optimized to provide the most localized set of WFs, maximally-localized Wannier functions (MLWFs) are obtained. Having a very localized representation of the electronic structure not only provides an insightful analysis of chemical bonding in solids, but also brings a formal connection between the MLWF centers and the modern theory of electric polarization. 

Moreover, the real-space locality of MLWF allows for accurate and fast interpolation of physical operators, enabling calculations of material properties that require dense samplings of the BZ, such as Fermi surface, orbital magnetization, anomalous Hall conductivity, and spin Hall conductivity, to name a few. 

However, obtaining accurate and compact MLWFs often requires chemical intuition and trial and error, a challenging step even for experienced researchers and a roadblock for high-throughput calculations. 

In this work, Junfeng Qiao et al. from the Theory and Simulations of Materials, École Polytechnique Fédérale de Lausanne, Switzerland, presented an automated method for the automated, robust, and reliable construction of tight-binding models based on MLWFs, projectability-disentangled Wannier functions (PDWFs). First, the authors chose physically-inspired orbitals as initial projectors for MLWFs, that is, the pseudo-atomic orbitals (PAOs) from pseudopotentials. 

Then, for each state, the authors decided if it should be dropped, kept identically, or thrown into the disentanglement algorithm depending on the value of its projectability onto the chosen set of PAOs. 

The authors augmented such projectability-based selection with an additional energy window to guarantee that all states around the Fermi level or the conduction band edge are well reproduced, showing that such a combination enables accurate interpolation even when minimal sets of initial atomic orbitals are chosen. 

They compared PDWFs with the other method that is also fully automated, namely SCDM. They showed with a detailed study of 200 structures that PDWFs lead to more accurate band interpolations, and are more atom-centered and more localized than those originating from SCDM. 

The method and workflows provided in this work is valuable for large-scale high-throughput findings of new materials and the insightful analysis of the related physical properties. Thisarticle was recently published in npj Computational Materials 9: 208 (2023).

原文Abstract及其翻译

Projectability disentanglement for accurate and automated electronic-structure Hamiltonians (精确和自动化电子结构哈密顿量的可投影解纠缠)

Junfeng Qiao, Giovanni Pizzi & Nicola Marzari 

Abstract

Maximally-localized Wannier functions (MLWFs) are broadly used to characterize the electronic structure of materials. Generally, one can construct MLWFs describing isolated bands (e.g. valence bands of insulators) or entangled bands (e.g. valence and conduction bands of insulators, or metals). Obtaining accurate and compact MLWFs often requires chemical intuition and trial and error, a challenging step even for experienced researchers and a roadblock for high-throughput calculations. Here, we present an automated approach, projectability-disentangled Wannier functions (PDWFs), that constructs MLWFs spanning the occupied bands and their complement for the empty states, providing a tight-binding picture of optimized atomic orbitals in crystals. Key to the algorithm is a projectability measure for each Bloch state onto atomic orbitals, determining if that state should be kept identically, discarded, or mixed into the disentanglement. We showcase the accuracy on a test set of 200 materials, and the reliability by constructing 21,737 Wannier Hamiltonians.

摘要

最大局域Wannier函数（MLWFs）被广泛用于表征材料的电子结构。通常，我们可以构建MLWFs来描述孤立能带（例如绝缘体的价带）或纠缠能带（例如绝缘体的价带和导带，或金属）。获得准确且紧凑的MLWFs通常需要化学直觉和反复试验，这即使对于经验丰富的研究人员来说也是一个挑战，且高通量计算也一个障碍。在这里，我们介绍了一种自动化方法，即可投影的解纠缠Wannier函数（PDWFs），它构建跨越占据带及其对应空态的MLWFs，提供了优化的晶体中原子轨道的紧束缚图像。该算法的关键是对每个布洛赫态在原子轨道上的可投影性度量，确定该状态应该保持不变，舍弃，还是混合进解纠缠中。我们在200种材料的测试集上展示了其准确性，并通过构建21,737个Wannier哈密顿量来证明其可靠性。