空间不确定性的表示与估计

 一、摘要

        本文介绍了一种估算温度的通用方法之间的标称关系和预期误差（协方差）表示对象相对位置的坐标框。这些帧只能通过一个简单的例子间接地知道一系列空间关系，每个关系都有其相关的错误，由多种原因引起，包括定位错误，测量误差或零件尺寸公差。这估算方法可用于回答以下问题：是否将摄像头连接到机器人上可能会有在其视野中的特定参照对象。计算的估计值与独立蒙特卡罗法的估计值吻合得很好卡洛模拟。这种方法使我们有可能做出正确的决定提前了解一段不确定的关系是否足够准确地完成某项任务，如果不足够，则了解一段不确定的关系的程度改进定位知识一个提议的传感器将提供。提出的方法可推广到六种自由度，并提供了一种实用的方法来估计、匹配对象，以及估算与关系。

二、介绍

       在许多应用中，有必要在对象之间空间关系的不准确信息的基础。例如，一个移动机器人需要对近似值进行说明和推理自身与其他对象之间的关系。此外，机器人必须能够使用传感器信息减少位置不确定性（位置和位置）方向）达到足以完成特定任务的程度。这个问题在实践中是复杂的因为一个对象相对于另一个对象的位置只能通过一系列的具有不确定性的相对参考系。在这个本文提出了一种显式表示的方法以及操纵与此相关的不确定性这些转变。我们还展示了传感器是如何工作的可以用来减少这种不确定性。这种形式主义使我们能够在给定电流的情况下提前估计机器人通过门的概率机器人和门位置的不确定性，摄像机视野中有物体的可能性，特定传感器是否具有完成特定任务所需的足够精度，等等。

        Brooks（1985）认为移动机器人使用全局参考系是不合适的。他认为通过不确定变换链接的一组局部参考框架更好。我们展示了如何估计一帧相对于另一帧的不确定性，以及如何将由于感测而减少的不确定性映射到任何帧，而不管感测在何处执行。由于这种灵活性，不需要特定的框架作为绝对参考。

        在以下各节中，我们将介绍如何估算三个自由度（x，y，8）的不确定性以移动机器人为例。作为机器人从一个地方到另一个地方，它的不确定性其相对于初始位置的位置会增长。我们提出了一种方法，用于对产生的误差进行定量估计，前提是移动是离散的如果机器人使用传感器（例如，声学范围（或视觉传感器）为了在它和其他物体之间进行相对测量，可以用于提高对全球位置的了解机器人和物体相对于任何坐标的坐标

        框架将它们连接在关系网络中（关系图）。因为估计和更新公式和相关程序只需要简单的矩阵计算，建议的方法是计算简单且快速。该理论假设导致错误的因素是“小的”，允许具有一阶误差模型的良好近似，传感器误差与位置误差无关。虽然给出的示例是针对移动机器人位置估计公式不确定性适用于许多其他领域。在里面事实上，这项工作最初是出于离线测量中不确定性的表现及原因工业机械手的编程应用。

三、基本估算操作

        不确定或近似变换（AT）由一个坐标系相对于另一个坐标系的估计平均关系和表示估计不确定性的协方差矩阵组成。ATs通常由相对运动或传感操作产生。术语A描述对象相对于某个定义坐标系的不确定相对位置（A）。

        用图表示。1-4，ATs用符号表示从参考坐标系到相对坐标系的箭头地点。以名义估算为中心的椭圆表示估算关系中的不确定性。椭圆是多变量高斯分布的常概率（二维）轮廓分布，并可用于约束实际位置应位于其中的高置信度区域建立虽然本文描述的程序对于估计ATs的平均值和协方差，不需要假设误差的高斯分布，有些当需要明确计算概率时，必须假设分布。第6.3节描述了假设基本高斯分布的基本原理在这种情况下的分布，附录A描述了如何从AT的估计协方差矩阵中提取椭圆参数。

        在本文中，我们介绍两种基本的操作这样就可以估计给定不确定的相对坐标系，任意两个坐标系连接它们的转换。第一种操作称为复合操作，它允许将一系列AT（递归）合并为一个AT。最终的复杂转型比以往更具不确定性它的组成部分。第二个操作称为合并，结合来自并行ATs的信息，生成一个单一合成AT，不确定度小于以下任何一种它的组成部分。

四、复合近似变换

        一个简单的机器人复合示例类似于Brooks（1985）中讨论的（见图1）。在本例中，机器人进行了多次移动并在其初始位置W附近结束(所有坐标在图1中，除了初始帧之外的帧被省略，以供参考机器人最终位置的不确定性关于W，如大的误差椭圆。实心误差椭圆表示相对误差机器人相对于其最后位置的不确定性，而虚线椭圆表示不确定性关于W的机器人的。请注意，机器人相对于世界位置的不确定性帧随着移动而增长。在第3节中，我们展示了如何计算复合ATs，例如E和G。

4.1 复合运算合并

        当有超过100%的人时，就会出现不同的情况一个独立于将利益框架与给定参考系。例如，如果机器人在图1从以下位置观察其起点（帧W）五十、 ，那么我们有两个AT从W到L4：（1）在G通过复合计算，以及（2）AT的倒数S由传感器给出。这两种转换是相互关联的通过加权平均（使用卡尔曼滤波）组合在第4）节中给出更多描述的公式准确估计L4相对于WAT S的误差（协方差）来自传感器的固有误差，而G的值来自于方程的复合协方差单个机器人动作A、B、C、D。给出了复合ATs的计算方法在第3节中，给出了合并ATs的方法在第4节。

        在本节中，我们描述了计算任意位置的标称位置和相关误差（表示为协方差矩阵）的复合程序相对于通过链接的任何其他对象的对象近似变换链（如图1）。这种方法不同于布鲁克斯提出的方法（1982年、1985年），他使用了错误。最大/最小方法假设最坏的情况当错误变得复杂且可能严重时的情况传播结果时高估错误通过几次转换。此外，最大/最小界限的解释也不清楚。做界限意味着观察是不可能的在他们之外，或者说这是不太可能的那么（如果是，可能性有多大）？所描述的方法由Chatila和Laumond（1985）为HILARE创作机器人与这里描述的机器人更相似；然而，他们使用了位置和位置的标量误差估计我们不关心角度误差。

4.2 复合公式

        （X3，Yy，G3）相对于参考框架W。我们正在复合变换A（X，Y，0）和B（X2，YI，02）。中给出了显式转换式（1）和是根据将一个框架转换为另一个框架的公式推导出来的，如Paul所示

(198 1). 例如

         我们希望估计平均数和协方差这三个功能。现在假设了这些变量是随机变量。这些函数用一阶泰勒级数展开近似变量的平均值。平均值函数（到一阶）是应用于变量意味着：例如，%= f（%，π，6，席，p2，和）。除了估计均值变换之外，AT还包括相关联的协方差矩阵这是一种转变。估计协方差矩阵对于这种情况，我们表示前面的泰勒矩阵形式的系列扩展，产生以下（偏离）矩阵：

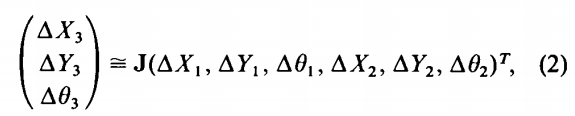
        其中J是变换的（3 X 6）雅可比矩阵根据变量的平均值进行评估：

        式（1）中给出了X3和Y3。定义了协方差当平方的期望值偏离时。我们将等式（2）的两侧乘以方程的边由它们各自的转置来表示。根据对结果的期望，我们得到协方差矩阵C3：

        3 X 3矩阵C3表示L2相对于W的坐标（即ATE） ，根据给定的协方差矩阵计算C、 和C，表示变量的误差（A和B）。因为协方差的一个元素矩阵定义为C，，=E（Ax，Ax，）和变量x的标准偏差为q=V（Ax2）an协方差矩阵的元素可以表示为：

        式中，pi是相关系数。对角线上在协方差矩阵中，i＝j；因此pi为1，C为只是差异。请注意，如果没有角度误差结合变量el和e2，我们可以减少H和K的维数以及相应的协方差矩阵。这是通过删除与6和6关联的行或列，。当没有考虑到角度误差，复合方程在随机变量中是线性的。结果这种情况下，理论上正确的值变换的一阶矩和二阶矩不是近似值。

        需要等式（1）和（4）来估计两种以上成分ATs的复合AT。该方法包括计算两个相邻的ATs并用该结果替换该对。任何一对连接的帧之间的AT可以是通过一系列这样的减少来计算。就是，一系列相对变换的结果可以是通过组合前两个变换来形成新的复合变换，然后将这一新的转变与第三个转变相结合转化成新的复合物，等等。例如，在图1中，A和B被复合以得到在E处，E和C复合得到F，和最后将F和D复合得到G。通过一个简单的链式规则参数，可以证明G的等价一阶估计是通过使用上述递归方法，或通过定义最终一次就所有变量而言的关系，以及求均值和协方差的一阶估计。显然，递归方法更简单。

        不确定关系的给定有向图可能不是上述公式所需的形式。例如，在图2A中，B指向相反方向指向上述假定形式的方向。创建正确的形式，必须先反转B，如中所示图2B。使用以下公式（逆变换）：

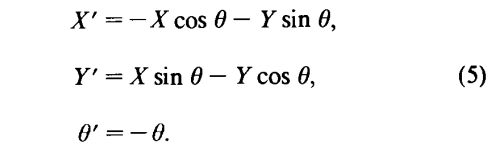
        如前所述，平均值的一阶估计虚线坐标的形式就是给定的函数平均变量的平均值。模型的协方差矩阵逆变换是根据给定的B的协方差矩阵（例如矩阵C）：

        其中R是上述变换的雅可比矩阵方程；也就是说，R由下式给出：

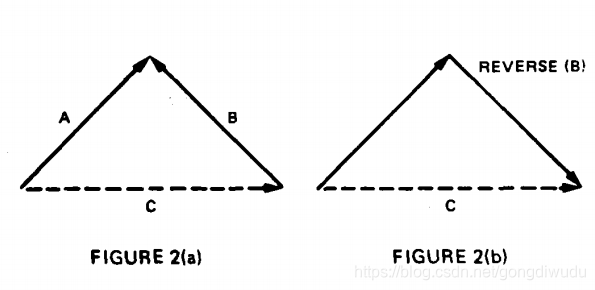
        R在X，Y和0处求值。同样，如果没有角度误差，我们可以省略R的行和列与6关联，并且所得协方差计算将是精确的。有了这个逆运算和上面给出的成对碰撞运算，就可以估计出任意两帧图像之间的化合物如图1所示，由一系列ATs链接的参考。

4.3 复合的假设

        这种复利操作背后的假设是：由式（2）表示的一阶近似值这是足够准确的。拟合成的ATs的误差是独立的。拟合成ATs的误差平均值为零。一阶近似是合理的变量的标准偏差（如ax）都很小，因为我们忽略了（02）~和泰勒级数展开式中的高阶。更多准确地说，函数应该是“平滑”的区间上的估计点，大致为变量标准偏差的大小。这种近似值可能会低估或高估误差协方差和估计的准确性取决于二阶（和）的重要性（更高）术语。

        连续ATs具有独立误差的假设意味着使用复合协方差非对角子矩阵为零的矩阵，如式（4）所示。如果已知这些误差是相关的，则可以直接给出具有非零协方差子矩阵的复合AT；也就是说，可以通过处理依赖的一对ATs作为一个单位，具有给定的复合协方差包含非零子矩阵的矩阵。系统或非零平均误差未建模。假设系统误差将通过适当的校准来消除。

五、近似变换的合并

        第二个基本操作是两个或多个对象的合并更平行的ATs，以获得更准确的估计关系的一部分。例如，在图1中，我们可以估计G，它表示L4关于框架W，我们在S描述了关于L4的W。我们面临的问题我们正在考虑的是如何估计L4的关系对于W，给定两个并行变换。我们用于合并的过程基于卡尔曼滤波方程（用于静态状态估计）。

5.1 合并公式

        第一步是找到所有链接帧的AT有意思。对于这些帧之间的每个独立变换链，估计合成在对于图1中的示例，必须计算G使用第3节中描述的方法进行估算L4相对于W的AT。下一步是确保要合并的所有并行ATs指向所需的方向，并反转这些方向但事实并非如此。在图1中，S应反转。AT的反转由等式给出(5） 及(六)。待合并的所有平行ATs完成后估计的（包括任何必要的逆转）合并过程使用最后一次合并的结果作为下一次合并的输入。合并从任意一对开始，然后继续进行将每个附加的AT与前面的结果合并直到所有ATs合并。因此，它是仅需描述成对合并过程。下面，让C和C7为协方差待合并ATs的矩阵，Ci为结果合并对的协方差矩阵。同样地，席和X2是估计要被合并的变换的平均值（表示为向量），以及是结果的估计平均值。第一步合并操作是计算卡尔曼增益系数定义如下：

        该系数用于计算所需的合并系数协方差矩阵

        平均是： 

         这些公式足以合并任意数量的并行ATs。方程的明显不对称性。（8） ，（9）和（10）不是真的，因为相同的结果是真的无论标记了哪个变换，都可以获得Ci或C2，等等。合并的顺序这些都是无关紧要的。在一个维度上，这些公式简化为以下简单形式（其中V为方差）：

        协方差矩阵简化为简单方差如图所示，合并后的平均值仅为贡献平均数的加权平均数。标量加权平均数的公式也被Chatila和Laumond（1985年）。如果复利第3节中描述的操作也减少到一个维，我们发现序列变换中的方差只是简单地相加得到复合方差。如果将这个结果和公式（1）结合起来，我们发现了与电路理论的相似性，其中方差为类似于电阻。也就是说，在电阻网络中，串联电阻通过加法和并联电阻根据公式（1）至（1）组合给出任意两个之间的组合阻力（方差）要点。在第5节中，我们将利用不确定性和阻力组合方式之间的相似性。

5.2 假设和合并

        介绍了卡尔曼滤波理论或状态估计在许多关于估计理论的文本中；推导基本公式很长，此处不提供（见Nahi 1976）。该理论的基本假设在这方面：待合并ATs中的错误是独立的。可以进行扩展来处理非依赖性ATs，当依赖性为鉴于合并两个平行ATs的公式被恰当地定义为加权线性组合这是两个估计数中的一个。如果要合并两个ATs具有高斯分布，已知组合它们并最小化的估计量均方估计误差具有线性关系表格（Nahi 1976）。此外，我们只估计每个AT分布的前两个矩（出于实际原因）。当未知概率分布的均值和方差为唯一可用的信息是，一个简单的最大熵推导给出高斯分布作为假设最小的分布信息。最后，线性形式通常用于估计量，并在实践中提供了一些良好的效果应用，包括导航（Gelb 1984）。误差是无偏的；即误差为零。这一假设排除了系统误差，系统误差通常通过适当的校准。