1、简写MRAS参考模型和可调模型
参考模型和可调模型方程:

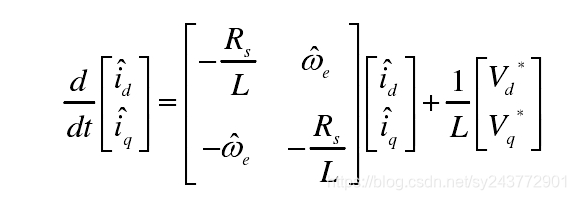
简写为如下形式:
参考模型:![]()
可调模型:![]()
定义广义误差为![]() ,将上述两个方程做差可以得到如下误差方程。
,将上述两个方程做差可以得到如下误差方程。
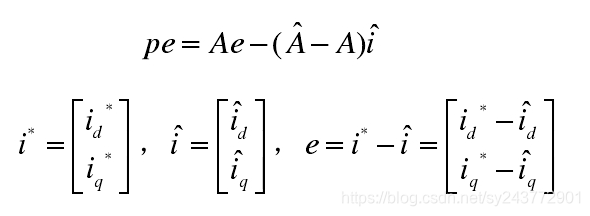
2、改写为标准前向环节
将上式改写为标准前向环节,方便对于Popov超稳定理论的分析。因为Popov超稳定理论规定了以下两个条件:
- 线性定常环节传递矩阵
 必须为严格的正实矩阵。
必须为严格的正实矩阵。 - 非线性时变反馈环节必须满足Popov积分不等式,即

改写为标准前向环节后的误差方程如下所示:

可以将其表示为下图所示结构:

3、满足Popov超稳定理论的自适应律设计
根据查阅文献可知,对Popov积分不等式逆向求解即可得到MRAS转速估计系统的自适应律。将误差方程带入到Popov积分不等式中时,可以得到:
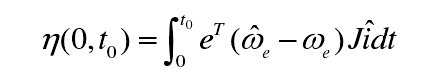
根据MRAS的基本结构,将估算速度we设计为比例积分的形式,

若能够证明此时的 we 是满足Popov超稳定理论,那么其就可以作为自适应律。证明过程如下:
将估计转速we带入到Popov积分不等式:

将其分解为:

如果上面两个均满足大于等于0,那么就可以证明稳定。

因此可以证明we比例积分形式满足Popov超稳定理论。因此可以对此进行自适应律提取:

将上式写成Pi的形式可得:
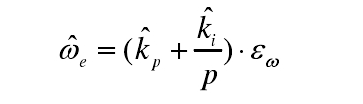
其中:
4、容易出错的点
这里讲一个比较容易出错的点,那就是下面这个方程,具体其id是什么,id^又是什么?

我们经过上面的推导,已经知道MRAS的基本观测原理。但是在这个地方,很多同学被以上物理公式混淆了。按照论文中给的这个公式,iq^就是如下公式设计的。但是其实论文中这么表示,极其的不严谨,此处的 id iq 是实际电机反馈的,那么此处的id^iq^也应该是电机反馈电流的估计值。而不是下面两张图这样归一之后的结果:

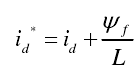
很多同学往往按照如下这张图去搭建MRAS观测器,结果发现怎么出来都不对。

其实事实上我们分析的时候可以这么分析,但是真的搭建仿真的过程中,还是要按照这个方程式来搭建:
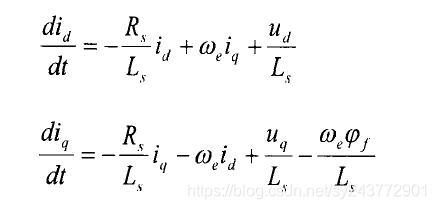
而这个估计出来id^才是这个公式里面的id^

最后以两张图来证实一下,正确的论文中的写法,两张图来自同一篇论文,所以一定要注意。
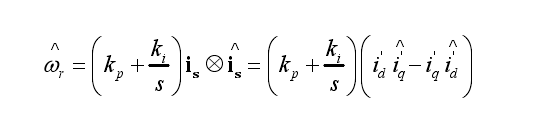

























 1086
1086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








