1. 背景
论文发表在2022IROS,是Patchwork的改进版本。算法通过数学方法进行快速而鲁棒性很强的地面分割,在智能机器人上的可操作性非常强。通过微调算法,可以应用于16-beams等多种规格的激光雷达。由于激光雷达点云数据标注的难度非常大,生产中自制数据集的成本很高,我做了一些对比实验,和RandLA-Net,Cylinder3D,GndNet,PVKD等机器学习模型进行比较,在分割地面这一任务上,用自制数据集测试,Patchwork++的表现远好于其他。
本文对 Patchwork 和 Patchwork++ 两篇论文作分析和介绍,简单讲述论文作者的思路和数学原理,最后展示根据需求修改后的算法表现效果——在不同设备上表现依然迅速稳健。
2. 摘要
传统数学方法,采用求反射梯度与地面对比的思路,对于高度有差别的平面难以识别(如低矮路沿),分割出的地面不是很合适。论文提出一种鲁棒性很强的分割方法,基于 Patchwork 的思路进行改进,自适应地调整参数,效果提升明显,运行速度极快。
3. 理论
Patchwork++ 的基本理论思路和 Patchwork 类似,下面将结合两篇论文,对方法中的每个步骤进行说明和讲解。

3.1. Problem Definition 问题定义
对地面分割做数学建模:对于所有的点云表示为,对点集进行二分类,分为G地面和N非地面,其中包括车辆,行人,植被,墙体等。其研究目标是最大化TP,最小化FN和FP,对于点集P可以有以下表示:
3.2. RNR: Reflected Noise Removal 反射噪声去除
思路:取出距离传感器较近的、高度小于某阈值,强度小于某阈值的数据点,这些点被认为是噪声点。实际情况下,由于激光雷达穿透效应,在地面以下偶尔也会产生噪声点,将其称为虚拟噪声,用一个自动更新的高度阈值,认为该阈值以下的点都为噪声,将其去除。

实现:维护两个阈值,高度阈值和强度阈值
,高度阈值在 A-GLE 环节自动更新。
需要自动更新,其原因在于如果采用固定值
,在向下陡坡的场景中,就会去除真实的地面点,造成数据缺失。如下图所示,(a) 表示GT,红色点表示为高度较低的地面;(b) 表示用定值 基于直接高度去除了真值(Patchwork方法);(c) 表示在 Patchwork 算法下造成了比较严重的欠分割情况;(d) 表示 Patchwork++ 算法维护一个自动更新的
,成功识别到了高度较低/下降坡度的地面。

3.3. CZM: Concentric Zone Model 同心区域模型
思路:用设计的扇区分割路面,用扇区拟合路面几何形态。基于路面非平坦假设,不应直接估计地面,而是通过假设非平坦地面有多个小块bin,在小块之内地面是平坦的。以往的方法用统一的极坐标系表示扇区S,再将扇区S划分为规则间隔的BIN。范用性不强,有以下两个缺陷:
- 稀疏问题:随距离增长,点云越发稀疏,难以找到正确的平面。
- 代表性问题:靠近原点的bin太小,难以表示扇区的空间特征,有时会导致扇区内地面法向量估计失败。
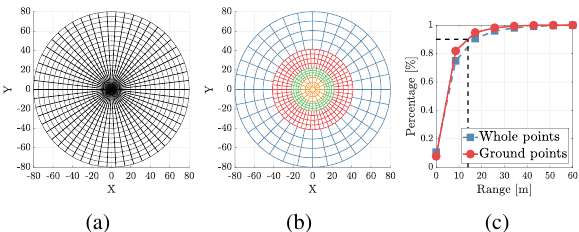
实现:以一种不增加计算复杂度的方式在bin之间分配适当的密度,数学模型如下:
全点集P被分为多个zone,每个zone由不同面积大小的bin组成,定义为:

其中,表示为zone,
表示zone的个数,那么
表示为:
![]()
和
表示
的最小和最大向径边界;同样被划分为多个
个bins,对于不同的zone,bin的大小也不同。在这里,
的定义为:
其中,,且
,对于全局最小边界
,其用于考虑移动平台或车辆附近的空旷情况。
实际实现,对于分别被称为中心区、四分之一区、半区和外区,统称为一个central zone,其中
的bin大小被设置的更大,以解决稀疏性问题和表示性问题。其计算方法为:
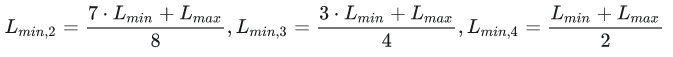
3.4. R-VPF: Region-wise Vertical Plane Fitting 区域垂直平面拟合
思路:由于路面可能存在一些高低差,在拟合时认为高程差不多的平面为同一个路面。拟合平面前,找到每个bin中的垂直点子集,将bin内的垂直平面找到并作过滤掉,拟合出更准确的平面。由于 PCA(点云主成分析)对于异常点敏感,经过这一步骤处理后可适用范围更广。

实现:利用 CMZ 分割得到的bin,设第n个bin为,通过以下4个步骤得到估计出的垂直点
:
以如下操作对bin进行k次迭代,挑选出足够的种子点集。
- 预选种子点集
进行k次迭代,每次迭代选取”一些”(论文原句)高度最低的点,求这些点的平均值,以及该子集的单位法向量
,代表 PCA 后最小特征值对应的归一化后的单位特征向量。
- 潜在垂直平面点集
对第k次迭代的种子点集,挑选出潜在的垂直平面点集
,公式如下:
![]()
其中,k = 1时,即种子点集为第n个bin的全部点。每次迭代时
,即上一次的种子点集减去之前迭代出的所有垂直点;
表示估计的垂直平面的距离阈值。
- 二值化验证点集
对第k次迭代的潜在垂直平面点集,二值验证出认为真正垂直的点集
,公式如下:

其中,表示z轴方向的单位法向量
,
是估计平面的单位法向量的阈值(点的法向量和z轴法向量做点乘,两个单位向量的点乘结果就是夹角的cos值,判断该值与90度的相近程度。在范围内,由这次迭代的潜在点找到的垂直点集,可以被认为是垂直点集;否则,这次的垂直点集,不能认为是垂直的)。
最后,累积所有的垂直点得到总的垂直点集,
表示总的迭代次数,公式如下:

3.5. R-GPF: Region-wise Ground Plane Fitting 区域地面拟合
思路:估计局部地面,将局部地面合并。对 R-VPF 处理后的各个bin进行PCA,取第三个特征代表高度特征。采用 PCA 在速度上至少比 RANSAC 快两倍,进行预处理后,效果类似。通俗来讲,设置一个阈值,每次迭代更新阈值,3次迭代后挑选出合适的地面种子点。
实现:对以上操作得到的bin进行计算,数学模型如下:
对zone内n个bin内的点集命名为,共计有
个这样的集合。如果一个 zone内有足够多的bin,即可以认为足够拟合平面,选取z最低的点作为种子点。令
作为
个种子点的z的平均值,则初始的地面的估计如下:
![]()
其中函数返回点的高度值,
表示种子点挑选高度阈值。第一次估计的地面点,是z高度不大于平均高度与高度阈值之和
的点集。
算法经过l次迭代计算出bin的地面拟合,第l次迭代的地面法向量为
。接着计算地面系数
:
![]()
其中,是第l次迭代,所有被分类为地面的点的平均值,用l次迭代得到的地面估计的平均点与法向量点乘,可以反映两个向量之间的投影值。第l+1次迭代的地面估计值计算公式为:
![]()
其中,,
表示平面高度阈值。实验证明,当
即进行3次迭代的效果最好。
3.6. A-GLE: Adaptive Ground Likelihood Estimation 自适应地面似然估计
思路:对上一步处理后得到的bin内种子点做处理,估计一个bin是否为地面。从 Uprightness 垂直度、Elevation 高程差
和 Flatness 平整度
三个方向设计。
实现:从Patchwork 的 GLE 步骤讲起,如下设计函数用于评估bin为是否为平面:

Uprightness :为了使
中大部分点都归属于地面(尽可能为TP),对每个zone的法向量
做如下操作:
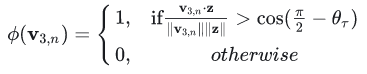
其中,,
为设置的角度阈值,这部分实际计算为bin内法向量与X-Y平面的夹角,当夹角趋于
时,意味着bin拟合的区域平面越平整。
在论文中被经验化地设置为
,即拟合出的区域平面的最大倾斜角度为
。
Elevation :为了解决高度不同的平面计算得到一样的垂直度,而误把一些建筑物或车辆顶部当作地面的误检,引入高程差计算项,具体如下:
其中为使
呈指数增长的自适应中点函数;如果
,即距离太远,则不予考虑,认为该平面仅由平整度和垂直度考虑。当bin的平均高度
时,即认为其为地面的可能性较高,输出值大于0.5;反之,认为其为地面的可能性较低,输出值小于0.5。
Flatness :为增加上坡地面的判断,利用高度判断的结果,对一些坡度较高的上坡地面进行拟合。

当时,地面已经足够平整,无需计算该项;当
时,需要判断其是否是可能的上坡路面。其中,
为一个设定的系数,目的是使得函数结果更明显;
表示bin的平整度,
为设定的平整度阈值,计算方法如下:

为bin的 PCA 特征,按降序排列。
最后,对所有bin统一以上三个方面,计算出整个点云的拟合平面,统计
的bin的集合,即为所拟合出的路面。

改进:不难发现,GLE 中设计了许多参数,根据不同环境需要有不同的选择;在选择参数时,尤其是在计算高程差所用的
、计算平整度
时所用的
非常耗时。Patchwork++论文基于 GLE 提出 A-GLE,为方便描述,将原先的
更换为
,即高程相关用e表示,平整度相关用f表示。

为解决该问题,Patchwork++论文基于 GLE 提出 A-GLE,一种自适应的参数调整方法,同时更新 RNR 步骤的高度阈值。
Elevation e:用 Definite Ground 表示 CZM 步骤中第m个zone,计算
满足平面拟合标准。
令为
中bin的
的集合,基于
,对高程标准阈值
进行更新:
![]()
其中,表示集合均值,
表示集合标准差,
为 CZM 中第m个ring的标准差修正增益,是定值。
Flatness f:由于将空间划分为bin,经过 PCA 计算得到的特征值和
是直接基于点云的,拟合出的平面会有坐标系未对齐的问题,导致平面拟合出现错误。这里对原先算法作纠正,直接用
平面法向量代替平整度估计。
类似的,令为
中
的集合,基于
,对平整度标准阈值
进行更新:
![]()
其中,表示 CZM 中第m个ring的标准差修正增益,是定值。
Noise Removal Height h:思路类似。
![]()
其中,表示距离传感器最近的一环zone中的种子点z的集合,
为需要移除的高度边界。
3.7. TGR: Temporal Ground Revert 临时地面还原
思路:对 A-GLE 处理后估计的地面进行纠正,恢复一些被误检的bin。一个bin内可能存在部分异常点使得地面拟合失效(例如崎岖的草地),计算值很可能超过阈值而导致错误估计。这是因为 A-GLE 是随时间推移依据所有的bin更新阈值,在当前时间更新的值会在下次被利用,但当前时间下的估计就会发生偏差;且采用均值加权更新,显然对于一些估计值偏大的bin会出现误检。
![]()
其中,为 CZM 第m个ring的标准差,是固定的值;
是
中平整度
的集,对于被拒绝的
的bin,如果其bin满足
,则被纠正为地面。

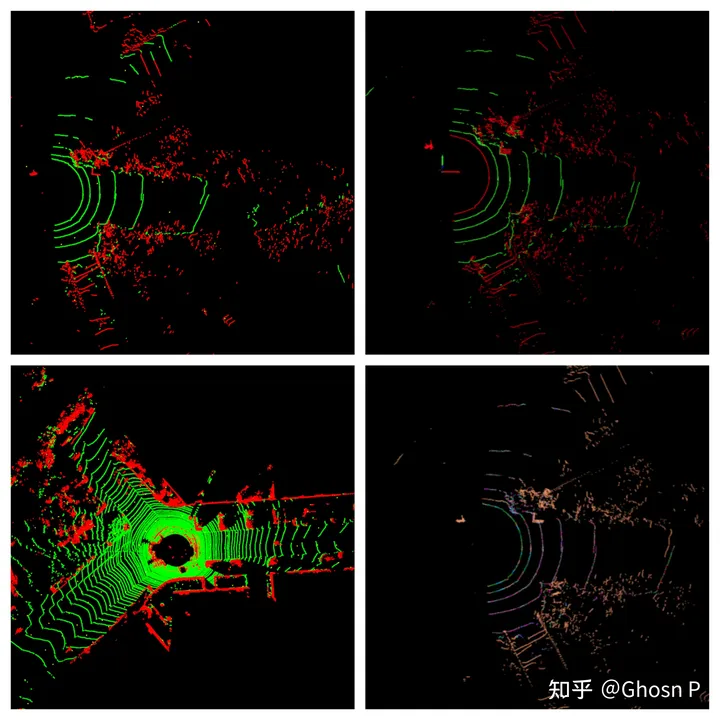
4. 表现
4.1. 论文数据


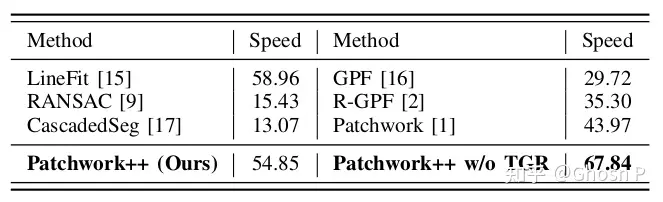
4.2. 自测表现
运行环境:
- OS: Ubuntu 20.04.6 LTS
- CPU: 12th Gen Intel® Core™ i7-12700H × 20
- GPU: NVIDIA GeForce RTX 3060 Laptop GPU
- Python: 3.6.13
- Open3D: 0.17.0
运行效果:
- 数据:Velodyne-Puck(VLP-16)在园区内采集。
- 速度:1.8ms-5.1ms,平均在2.6ms。
- 表现:粗略统计,在自制数据集上测试,80%以上的场景在20m半径内正确分割路面,95%以上的场景在10m半径内正确分割路面。
参考文献
Patchwork: Concentric Zone-based Region-wise Ground Segmentation with Ground Likelihood Estimation Using a 3D LiDAR Sensor
Patchwork++: Fast and Robust Ground Segmentation Solving Partial Under-Segmentation Using 3D Point Cloud
论文分享:Patchwork++/Patchwork-基于点云的快速稳健地面分割算法 - 知乎
























 2897
2897

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








