【射影几何05】齐次坐标系（Homogeneous coordinates）

无水先生

已于 2023-07-27 22:36:45 修改

阅读量7.4k

点赞数 1

分类专栏： # 射影几何和slam基础文章标签：几何学

于 2022-04-01 09:24:03 首次发布

本文链接：https://blog.csdn.net/gongdiwudu/article/details/123129067

版权

射影几何和slam基础专栏收录该内容

19 篇文章

订阅专栏

一、说明

本章建立射影几何的坐标系，如何建立坐标系？回答，建立坐标系方法不止一种，其中齐次坐标系是一种方法。

二、齐次坐标的历史

在数学中，齐次坐标或射影坐标由 August Ferdinand Möbius 在其 1827 年的著作 Der barycentrische Calcul 中引入，是射影几何中使用的坐标系统，就像在欧几里得几何中使用笛卡尔坐标一样。它们的优点是可以使用有限坐标表示点的坐标，包括无穷远处的点。涉及齐次坐标的公式通常比笛卡尔对应的公式更简单、更对称。齐次坐标具有一系列应用，包括计算机图形学和 3D 计算机视觉，它们允许仿射变换，一般来说，投影变换可以很容易地用矩阵表示。

奧古斯特·費迪南德·莫比烏斯 (August Ferdinand Möbius)

奧古斯特·費迪南德·莫比烏斯，德國數學家和天文學家，被認為是拓撲學的先驅。莫比烏斯最著名的成就是發現了三維歐幾里得空間中的一種奇特的二維單面環狀結構——後人稱為莫比烏斯帶。其他重要的成就包括在射影幾何中引進齊次坐標系、莫比烏斯變換，數論中的莫比烏斯變換、莫比烏斯函數、莫比烏斯反演公式等等。

莫比乌斯

如果一个点的齐次坐标乘以一个非零标量，那么得到的坐标代表同一个点。由于齐次坐标也被赋予无限远的点，因此允许这种扩展所需的坐标数比所考虑的投影空间的维数大一。例如，需要两个齐次坐标来指定投影线上的一个点，而需要三个齐次坐标来指定投影平面上的一个点。

三、建立其次坐标系

取定普通平面上直角坐标系,点的坐标用数组( x, y)表示,其中 x, y 可取一切实数.所有的数组( x, y)所成的集合与平面上的点是一一对应的,为了表示无穷远点,我们引进齐次坐标.

3.1 齐次坐标定义

定义：如果点 P 的直角坐标是( x, y),那么称( x1 , x2 , x3 )是 P 的齐次坐标,其中 x1 , x2 , x3 满足 $\large x = x_1/x_3$ , $\large y = x_2/x_3$ , $\large x_3\neq 0$ .

也就是说，在X-Y坐标平面的点，将其阔维，成为X-Y-Z坐标，而原来的（x，y）点，如今成为（x，y，1）点；而新坐标的点（mx，my，m）依然指的是（x，y，1）点。

从另一个角度，将O（0，0，0）点看成射影点，那么从O发出的任意射线上所有的点，统统映射到平面上一个点，而且坐标是等价于平面（X，Y，1）上的点坐标。其中OS=1；

3.2 齐次坐标的合理性解释

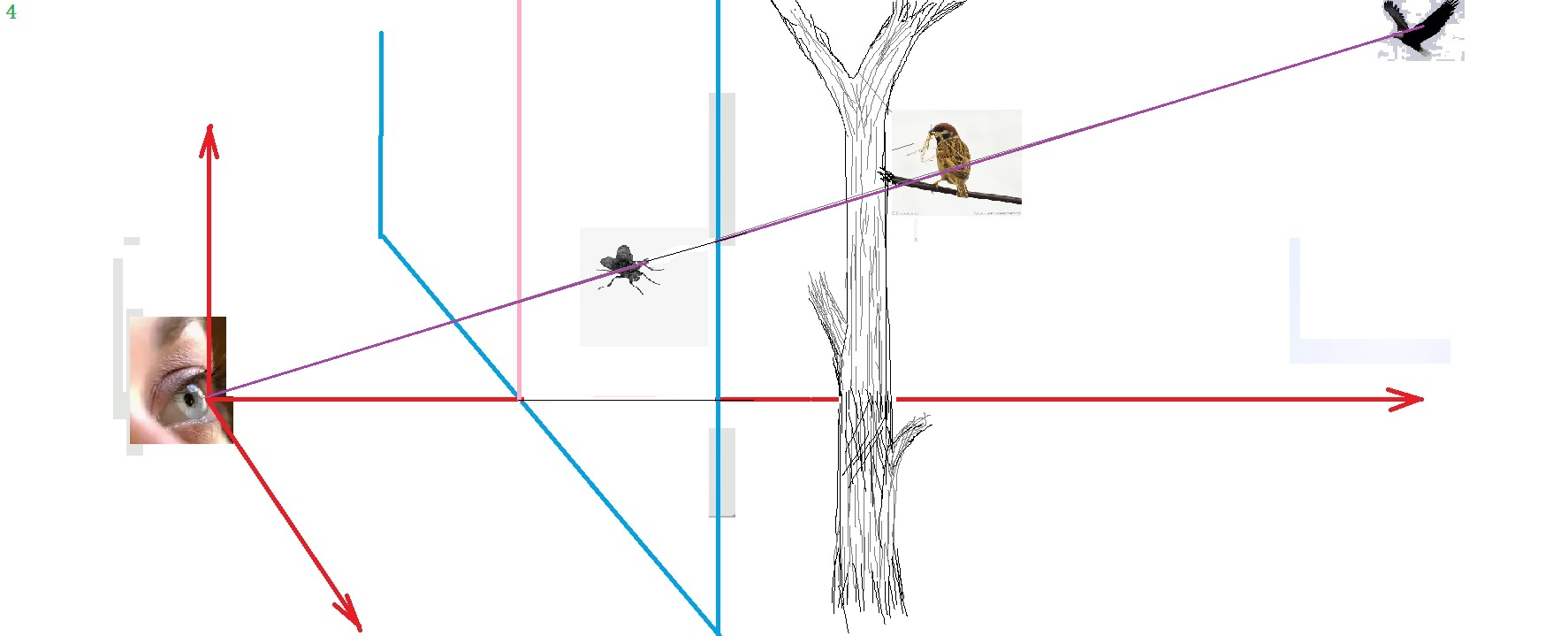
如图：在三维坐标的原点处（0，0，0）有人眼观望，距离人眼1米处有一块玻璃（蓝色）；玻璃上任意点坐标为（x，y，1）；有苍蝇站在玻璃上，坐标为（x0，y0，1）其观察角度，正好是苍蝇、小鸟、苍鹰在相同直线上；不难想象，看到苍蝇在小鸟上，而小鸟在苍鹰上；这很符合生活实际，因此，小鸟的实际位置为（mx0，my0，m）苍鹰坐标为（nx0，ny0，n），由于我们只关注玻璃上的二维世界，因此，无论苍蝇（x0，y0，1），小鸟（mx0，my0，m）、苍鹰（nx0，ny0，n）的具体坐标不同，在玻璃立场上，这些坐标都能还原成（x0，y0，1）。因此，顺着直线（sx ，sy ，s）的所有点，在玻璃上的坐标是唯一的，即（x，y，1）。