独立事件、笛卡尔积与矩阵向量乘法

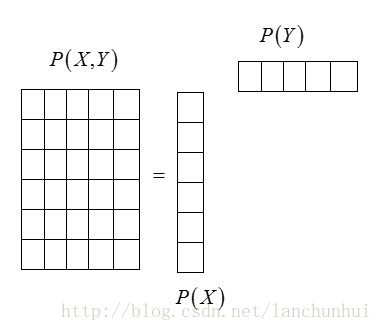
$X,Y$ 为离散型随机变量，$X$ 有 6 种可能的状态（值），$Y$ 有 5 种可能的状态。以上的 $P(X,Y) = P(X)\cdot P(Y)$，则对应着如下的三种含义：

• 独立事件的联合概率（joint distribution）
• 笛卡尔积
• 矩阵向量乘法：$C_{6\times 5}=A_{6\times 1}\cdot B_{1\times 5}$

1. 笛卡尔积（Cartesian product）

$$A\times B=\{(a,b)|a\in A\; \text{and}\;b \in B\}$$

笛卡尔积并非是笛卡尔本人发明的数学概念，而是后世数学家在定义两个集合的二元关系时，仿照笛卡尔坐标系（这个是笛卡尔天才的发明），而定义的名字。

换句话说，笛卡尔坐标系其实对应着一种笛卡尔乘积；