因子图学习笔记其一

Reference:

1. Frank Dellaert 《机器人感知-因子图在SLAM中的应用》

1. 引言

1.1 机器人领域中的推断问题

为了使机器人在现实世界中灵活地运动，需要基于先验知识，通过其传感器推断出关于外部世界的信息。

在 SLAM 问题中，目标是利用机器人传感器收集到的信息对机器人自身进行定位。在简单的情况下，传感器测量到的信息可能是路标点(Landmark)的方位。如果路标点位置已知，那么这个问题就退化为一个经典的三角化问题-----船在海上如何进行导航。然而，SLAM 问题中的难点在于，无法提前知道路标点的位置，因此，不得不在利用已有地图进行定位的同时，建立新的地图(意思是又要建图，又要在已有地图上定位吧)。

1.2 概率模型

由于测量具有不确定性，所以我们不可能恢复出外部世界的真实状态(有偏差)，但是可以从测量中推断出关于外部世界真实状态的一个概率描述。这里使用贝叶斯概率对不确定的事件分配一个主观的置信度。

在机器人领域中，通常需要对连续多元随机变量 $\mathbf{x}\in {\mathbb{R}}^n$ 的置信度进行建模。我们通过变量 $\mathbf{x}$ 的概率密度函数(PDF) $p(\mathbf{x})$ 来建模，变量 $\mathbf{x}$ 满足(概率和为$1$)：
$$\int p(x)\mathrm{d}\mathbf{x}=1$$

小写字母代表随机变量，大写字母代表随机变量的集合。

下面将未知变量 $\mathbf{X}$ 的含义具体化。在 SLAM 问题中，当给定一个观测量集合 $\mathbf{Z}$时，未知变量 $\mathbf{X}$ 为机器人的位姿和未知的路标点位置。用贝叶斯概率的语言来描述的话，这就是简单的条件概率密度:
$$p(\mathbf{X}\mid \mathbf{Z})$$

经典的 SLAM 模型通常由一个运动方程和一个观测方程构成，如下所示：
$$\{\begin{array}{l}{\mathbf{x}}_k=f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{w}}_k\\ {\mathbf{z}}_{k,j}=h\left({\mathbf{y}}_j,{\mathbf{x}}_k\right)+{\mathbf{v}}_{k,j}\end{array}$$

得到这个条件概率密度的过程称为概率推断。为了给感兴趣的变量指定一个概率模型，并明确这些变量如何影响 (具有不确定性的) 测量值，这里我们引入了概率图模型。

概率图模型通过探索复杂概率密度函数内部的结构，提供了一种对其进行描述的紧凑方式。特别地，高维概率密度函数通常可以被分解为很多因子的乘积，其中每个因子都是一个更小范围内的概率密度。后文再介绍具体概念。

1.3 贝叶斯网络

因为通常利用传感器生成观测量非常容易，所以在机器人领域中，贝叶斯网络是一种对机器人推断问题进行建模的方便的图模型语言。比如，如果有人告诉我们路标点的位置、机器人的位姿，以及机器人上面配置的传感器之间的相对几何关系，就很容易预测观测量是什么。观测量预测和噪声模型是生成模型中的核心要素，这与贝叶斯网络架构很好地匹配了起来。

贝叶斯网络是一个有向图模型，图中的节点代表变量 ${\theta }_j$。我们将全部感兴趣的随机变量集合表示为 Θ = { θ 1 ⋯ θ n } \boldsymbol{\Theta}=\left\{\theta_1 \cdots \theta_n\right\} Θ={θ1​⋯θn​}。 一个贝叶斯网络在所有的变量 $\mathbf{\Theta }$ 上的联合概率密度函数 $p(\mathbf{\Theta })$ 被定义为与每个节点相关联的条件概率密度的乘积：
$$p(\mathbf{\Theta })\stackrel{\text{ def }}{=}\prod _{j}p\left({\theta }_j\mid {\pi }_j\right)$$

式中，$p\left({\theta }_j\mid {\pi }_j\right)$ 是节点 ${\theta }_j$ 的条件概率密度函数，${\pi }_j$ 是 ${\theta }_j$ 的父节点。在一个贝叶斯网络中，联合概率密度的分解由其图结构，特别是它与父节点之间的关系所决定。

示例

左下图给出一个小型 SLAM 的例子。一个机器人在 $3$ 个连续位姿 ${\mathbf{x}}_1$、${\mathbf{x}}_2$ 和 ${\mathbf{x}}_3$ 下，对 $2$ 个路标点 ${\mathbf{l}}_1$ 和 ${\mathbf{l}}_2$ 进行观测。为了得到路标点的绝对坐标，我们假定在第一个位姿 ${\mathbf{x}}_1$ 处，有一个绝对位置/朝向(位姿)的观测量。如果没有这个假设，也就没有了关于绝对位置的任何信息，因为方位 (角) 测量值都是相对量(所以右下有个${\mathbf{z}}_1$，需要知道初始位置来求得绝对位置)。

考虑左上图的贝叶斯网络。感兴趣的随机变量是 Θ = { X , Z } \boldsymbol{\Theta}=\{\boldsymbol{X}, \boldsymbol{Z}\} Θ={X,Z}，即未知的机器人位姿和路标点位置 $\mathbf{X}$，以及观测量 $\mathbf{Z}$ 。这样就可以得到右上图，被观测到的观测量显示在矩形节点中。按照通常的贝叶斯网络的定义，联合密度函数 $p(\mathbf{X},\mathbf{Z})=p\left({\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,{\mathbf{l}}_1,{\mathbf{l}}_2,{\mathbf{z}}_1,{\mathbf{z}}_2,{\mathbf{z}}_3,{\mathbf{z}}_4\right)$ 可由一系列条件概率密度函数的乘积得到(也就是可以得到每个路标和机器人，在各位姿下的概率，目标是最后使用一个最大概率的作为最终结果):
$$\begin{array}{rl}p(\mathbf{X},\mathbf{Z})& =p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)\\ & \times p\left({\mathbf{l}}_1\right)p\left({\mathbf{l}}_2\right)\\ & \times p\left({\mathbf{z}}_1\mid {\mathbf{x}}_1\right)\\ & \times p\left({\mathbf{z}}_2\mid {\mathbf{x}}_1,{\mathbf{l}}_1\right)p\left({\mathbf{z}}_3\mid {\mathbf{x}}_2,{\mathbf{l}}_1\right)p\left({\mathbf{z}}_4\mid {\mathbf{x}}_3,l_2\right)\end{array}$$

可以看出，这个例子中的联合概率密度函数包含 $4$ 个性质不同的因子集合：

• 一个在位姿 ${\mathbf{x}}_1$、${\mathbf{x}}_2$ 和 ${\mathbf{x}}_3$ 上的 “马尔可夫链” $p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)$。条件概率密度函数 $p\left({\mathbf{x}}_{t+1}\mid {\mathbf{x}}_t\right)$ 可从先验知识或者已知的控制输入中推导出来。
• 路标点 $l_1$ 和 $l_2$ (在 SLAM 的设置中，当没有先验地图时，通常会被省略) 上的先验概率密度函数 $p\left(l_1\right)$ 和 $p\left(l_2\right)$。
• 在第一个机器人位姿 $x_1$ 处路标点绝对位姿观测的条件概率密度函数 $p\left(z_1\mid x_1\right)$。
• $3$ 个条件概率密度函数的乘积 $p\left(z_2\mid x_1,l_1\right)p\left(z_3\mid x_2,l_1\right)p\left(z_4\mid x_3,l_2\right)$，分别对应于在 $3$ 个位置 ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3$ 对路标点 ${\mathbf{l}}_1$ 和 ${\mathbf{l}}_2$ 的 3 个方位 (角) 的观测量的条件概率密度函数。

注意，图模型的结构明确地说明了数据之间的关联 ( data association)，即，对于每一个观测量 $z_k$, 我们都知道它来自对哪个路标点的观测。

1.4 指定概率密度函数

上面所说的概率密度函数的直接形式非常依赖于具体的应用及所使用的传感器。最常用的概率密度分布是多元高斯分布，未知量的先验通常被指定为高斯密度函数。多元高斯分布的概率密度函数如下:
$$\mathcal{N}(\theta ;\mu ,\Sigma )=\frac{1}{\sqrt{|2\pi \Sigma |}}\exp \left\{-\frac{1}{2}\Vert \theta -\mu {\Vert }_{\Sigma }^2\right\}$$

式中，$\mathbf{\mu }\in {\mathbb{R}}^n$ 是均值，$\mathbf{\Sigma }$ 是一个 $n\times n$ 的协方差矩阵，并且($\stackrel{\text{ def }}{=}$表示等价于，是一个东西。更详细的可以看之前写的 非线性优化)：
$$\Vert \theta -\mu {\Vert }_{\Sigma }^2\stackrel{\text{ def }}{=}(\theta -\mu {)}^{\top }{\Sigma }^{-1}(\theta -\mu )$$

表示马氏距离(mahalanobis distance) 的平方。

在许多情况下，我们都认为测量值受到均值为零的高斯噪声干扰。例如，在一个给定位姿 $\mathbf{x}$ 下观测一个给定的路标点 $\mathbf{l}$，得到的方位 (角) 测量值会被建模为
$$z=h(x,l)+\eta$$

式中，$h(\cdot )$ 是观测预测函数(measurement prediction function)，噪声 $\eta$ 由协方差矩阵为 $\mathbf{R}$ 的零均值高斯分布(有两个地方注意:1.假设的协方差矩阵是零均值的 2.将协方差矩阵$\Sigma$具体化为了$R$)所描述。对于观测量 $\mathbf{z}$，条件概率密度函数 $p(z\mid x,l)$ 如下：
$$p(z\mid x,l)=\mathcal{N}(z;h(x,l),R)=\frac{1}{\sqrt{|2\pi R|}}\exp \left\{-\frac{1}{2}\Vert h(x,l)-z{\Vert }_R^2\right\}$$

在实际的机器人应用中，观测函数 $h(\cdot )$ 通常是非线性的。一个二维的方位(角)测量的观测函数简单表示如下(一般用的不是方位测量，视觉里程计是转换到图像上的位置)：
$$h(\mathbf{x},\mathbf{l})=\mathrm{atan}2\left(l_y-x_y,l_x-x_x\right)$$

式中，atan2 是反正切三角函数。因此，最终的概率观测模型(probabilistic measurement model)$p(\mathbf{z}\mid \mathbf{x},\mathbf{l})$ 可由下式表示(这里把角度作为了感兴趣的随机变量$\theta$)：
$$p(z\mid x,l)=\frac{1}{\sqrt{|2\pi R|}}\exp \left\{-\frac{1}{2}{\Vert \mathrm{atan}2\left(l_y-x_y,l_x-x_x\right)-z\Vert }_R^2\right\}$$

我们不会一直假设观测噪声符合高斯分布。为了处理偶然的数据关联误差，许多作者提出使用鲁棒观测概率密度分布，其概率分布曲线具有比高斯分布更长的“尾巴”。

并不是所有的概率密度函数都是由观测数据推导而来。例如，在之前的小型 SLAM 问题中的概率密度函数 $p\left({\mathbf{x}}_{t+1}\mid {\mathbf{x}}_t\right)$，指定了一个概率运动模型(probabilistic motion model)，并且假定机器人会按照这个模型来运动。概率运动模型可以直接按照上面描述的方式，从里程计观测中推导出来。运动模型也可以从已知的控制输人 ${\mathbf{u}}_t$ 得到。在实际情况中，我们经常使用条件概率高斯假设：
$$p\left({\mathbf{x}}_{t+1}\mid {\mathbf{x}}_t,{\mathbf{u}}_t\right)=\frac{1}{\sqrt{|2\pi Q|}}\exp \left\{-\frac{1}{2}{\Vert g\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)-{\mathbf{x}}_{t+1}\Vert }_Q^2\right\}$$

式中，$g(\cdot )$ 是运动模型，$Q$ 是协方差矩阵。例如，在一个平面上运动的机器人的例子中，$Q$ 的维度为 $3\times 3$ 。要注意，对于在三维空间中运动的机器人来说，需要稍微复杂一点的机制去描述在非线性流形（比如 SE(3) ) 上的概率密度。

上文讲到了两个比较重要的模型，1.概率观测模型；2.概率运动模型。
分别对应前文写过的：
$$\{\begin{array}{l}{\mathbf{x}}_k=f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{w}}_k\\ {\mathbf{z}}_{k,j}=h\left({\mathbf{y}}_j,{\mathbf{x}}_k\right)+{\mathbf{v}}_{k,j}\end{array}$$

1.5 在贝叶斯网络中进行模拟

当一个概率模型被指定为贝叶斯网络时，在其中进行模拟就变得非常容易。这就是很多生成模型选择使用贝叶斯网络进行描述的原因，通常在构建模型时使用贝叶斯网络具有很多优势。

具体说来，要想对 $P(\mathbf{\Theta })\stackrel{\text{ def }}{=}{\prod }_{j}P\left({\mathbf{\theta }}_j\mid {\mathbf{\pi }}_j\right)$ 进行模拟，只需对图中的节点进行拓扑排序，并按照如下规则进行采样：所有的父节点 ${\mathbf{\pi }}_j$ 的值都在从条件概率密度 $P\left({\theta }_j\mid {\mathbf{\pi }}_j\right)$ 中对 ${\theta }_j$ 进行采样之前生成，这个技术被称为原始采样法(ancestral sampling)。

仍旧以小型 SLAM 问题为例来分析。即使在这个小型的问题中，也很容易看到，对联合概率密度的分解可以使我们进行局部采样，而不必全局地解决问题。在上面示例的贝叶斯网络中对联合概率密度 $p\left(x_1,x_2,x_3,l_1,l_2,z_1,z_2,z_3,z_4\right)$ 进行模拟采样:

1. 从 $p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)$ 中对位姿 ${\mathbf{x}}_1$、${\mathbf{x}}_2$ 和 ${\mathbf{x}}_3$ 进行采样，模拟一个机器人轨迹。
2. 从 $p\left(l_1\right)$ 和 $p\left(l_2\right)$ 中对路标点 $l_1$ 和 $l_2$ 进行采样，生成一些模拟的路标点。
3. 从条件概率密度 $p\left(z_1\mid x_1\right)$、$p\left(z_2\mid x_1,l_1\right)$、$p\left(z_3\mid x_2,l_1\right)$ 和 $p\left(z_4\mid x_3,l_2\right)$ 中对观测量进行采样，模拟机器人的传感器观测值。

也可以用其他的拓扑排序方式。例如，可以将步骤 1 和步骤 2 进行调换，而不会引起任何不良的后果。并且，在位姿 ${\mathbf{x}}_1$ 生成之后的任何时间点，我们都可以生成关于位姿 ${\mathbf{x}}_1$ 的观测 ${\mathbf{z}}_1$ 。

1.6 最大后验概率推断

我们已经掌握了对外部世界进行建模的方法，当获得关于外部世界的信息时，就可以对有关外部世界的知识进行推断。我们也已经看到了如何以贝叶斯网络的方式来指定一个联合概率密度 $P(\mathbf{\Theta })$：根据图结构进行分解，并且根据相关的先验和条件概率密度得到直接的计算公式。

在机器人领域中，我们通常比较关心在给定观测 $\mathbf{Z}$ 的情况下，对末知的状态变量 $\mathbf{X}$ (位姿或陆标点) 的估计。对于这些末知的状态变量 $\mathbf{X}$，最常用的估计器是最大后验概率估计(maximum a posteriori estimate)。之所以命名为最大后验概率估计，是因为它在给定了观测 $\mathbf{Z}$ 的情况下，最大化状态 $\mathbf{X}$ 的后验概率密度 $p(\mathbf{X}\mid \mathbf{Z})$：

$$\begin{array}{rl}{\mathbf{X}}^{\text{MAP }}& =\underset{\mathbf{X}}{\mathrm{argmax}}p(\mathbf{X}\mid \mathbf{Z})\\ & =\underset{\mathbf{X}}{\mathrm{argmax}}\frac{p(\mathbf{Z}\mid \mathbf{X})p(\mathbf{X})}{p(\mathbf{Z})}\end{array}$$

上式利用了贝叶斯法则，将后验概率密度表示为观测概率密度 $p(\mathbf{Z}\mid \mathbf{X})$(似然) 与状态变量的先验概率密度 $p(\mathbf{X})$ 的乘积，再利用因子 $p(\mathbf{Z})$ 进行归一化。

然而，贝叶斯法则还有一种不同的表达方式，可以让我们更好地理解最大后验概率推断下的真实计算过程。实际上，式 $\underset{\mathbf{X}}{\mathrm{argmax}}\frac{p(\mathbf{Z}\mid \mathbf{X})p(\mathbf{X})}{p(\mathbf{Z})}$ 所示贝叶斯法则中的各项理论上可以从贝叶斯网络中计算得到。然而，当给定观测 $\mathbf{Z}$ 时，归一化项 $p(\mathbf{Z})$ 就与最大后验概率无关，可以被忽略。另外，由于条件概率密度 $p(\mathbf{Z}\mid \mathbf{X})$ 是 $\mathbf{Z}$ 中归一化的高斯概率密度函数，我们只在它作为位置状态量 $\mathbf{X}$ 的函数时才关心它。因此，贝叶斯法则的第二种，同时也是更重要的一种表达形式如下:
$${\mathbf{X}}^{\text{MAP }}=\underset{\mathbf{X}}{\mathrm{argmax}}l(\mathbf{X};\mathbf{Z})p(\mathbf{X})$$

这里，$l(X;Z)$ 是给定观测 $Z$ 的情况下状态量 $\mathbf{X}$ 的似然估计，被定义为任意一 个与 $p(\mathbf{Z}\mid \mathbf{X})$ 成正比的函数:
$$l(\mathbf{X};\mathbf{Z})\propto p(\mathbf{Z}\mid \mathbf{X})$$

符号 $l(\mathbf{X};\mathbf{Z})$ 强调了一个事实：似然估计是一个关于 $\mathbf{X}$ 的函数，而不是关于 $\mathbf{Z}$ 的函数。

我们要意识到，在观测上进行条件化，所生成的似然函数与高斯概率密度分布并不相似。为了看到它的具体形式，让我们再次考虑1.4节中二维方位 (角) 的观测概率密度函数。将它写成一个似然函数的形式，可以得到：
$$l(\mathbf{x},\mathbf{l};\mathbf{z})\propto \exp \left\{-\frac{1}{2}{\Vert \mathrm{atan}2\left(l_y-x_y,l_x-x_x\right)-\mathbf{z}\Vert }_R^2\right\}$$

式中，只有 $\mathbf{z}$ (在归一化后) 服从高斯分布，其他变量并不服从高斯分布。即使在观测函数是线性的情况下，观测量 $\mathbf{z}$ 也往往比它所依赖的未知变量的维度要低。因此，即使是最好的情况，观测上的条件也只能生成一个关于未知量的退化高斯密度函数。只有当我们融合了多个观测的信息后，未知变量才有一个好的概率密度函数。在没有足够多的观测来限制所有变量的情况下，最大后验概率推断将失败，因为此时不存在一个唯一的最大化的后验概率 ${\mathbf{X}}^{\text{MAP }}=\underset{\mathbf{X}}{\mathrm{argmax}}l(\mathbf{X};\mathbf{Z})p(\mathbf{X})$。

以上所有内容都指向了 $1.7$ 节关于因子图的介绍。之所以介绍一种新的图模型语言，是因为：
(a) 状态量 $\mathbf{X}$ 与观测量 $\mathbf{Z}$ 之间明显的划分；
(b) 我们对于非高斯似然函数更感兴趣，而它并不是一个有效的概率密度分布。因此，贝叶斯网络语言与我们遇到的实际优化问题的错位非常严重。我们将在第3章看到，因子图结构与解决大规模推断问题的计算策略有着非常紧密的联系。

1.7 因子图推断

贝叶斯网络是一种非常适合用于建模的语言，相比而言因子图则更适合用于推断。像贝叶斯网络一样，因子图允许我们将一个联合概率密度表示为一系列因子的乘积。然而因子图比贝叶斯网络更加通用，因为它不仅可以指定概率密度，还可以指定在变量 $\mathbf{X}$ 的集合上的任意一个因子函数 $\varphi (\mathbf{X})$。

为了进行更深人的探讨，我们考虑在小型 SLAM 例子上进行最大后验概率推断。考虑到未知量依赖于观测量 $\mathbf{Z}$，可以利用贝叶斯法则${\mathbf{X}}^{\text{MAP }}=\underset{\mathbf{X}}{\mathrm{argmax}}\frac{p(\mathbf{Z}\mid \mathbf{X})p(\mathbf{X})}{p(\mathbf{Z})}$将后验概率 $p(\mathbf{X}\mid \mathbf{Z})$ 重写为如下形式(和1.3节中的联合密度函数大差不差)：
$$\begin{array}{rl}p(\mathbf{X}\mid \mathbf{Z})& \propto p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)\\ & \times p\left({\mathbf{l}}_1\right)p\left({\mathbf{l}}_2\right)\\ & \times l\left({\mathbf{x}}_1;{\mathbf{z}}_1\right)\\ & \times l\left({\mathbf{x}}_1,{\mathbf{l}}_1;{\mathbf{z}}_2\right)l\left({\mathbf{x}}_2,{\mathbf{l}}_1;{\mathbf{z}}_3\right)l\left({\mathbf{x}}_3,{\mathbf{l}}_2;{\mathbf{z}}_4\right)\end{array}$$

很显然，上面的式子仅仅表示了在未知变量上一个没有被归一化的因子的概率 密度。

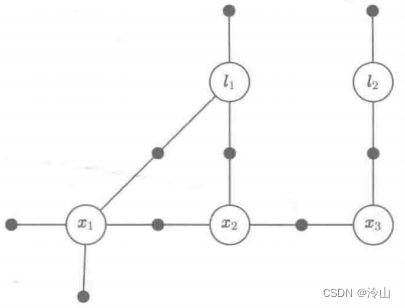
为了使这个因式分解更加明确，我们使用了因子图(factor graph)。下图引入了与上面例子相对应的因子图：与贝叶斯网络一样，所有的未知状态量 $\mathbf{X}$，包括机器人位姿和路标点，都用一个节点表示。然而，与贝叶斯网络不同的是，观测量并不会被显式地表示出来，我们对它不感兴趣。在因子图中，并不是每一个节点都有一个条件概率密度，而是显式地使用一种新的节点类型-----因子(factor)，去表示每一个后验概率密度 $p(\mathbf{X}\mid \mathbf{Z})$。在图中，每一个黑色节点代表一个因子，因子节点只与其观测函数中出现的状态变量节点相连接。例如，似然因子 $l\left({\mathbf{x}}_3,l_2;z_4\right)$ 只与变量节点 $x_3$ 和 $l_2$ 相连接。以此作为指导原则，可以很容易地将因子图中的 9 个因子节点与后验概率密度 $p(\mathbf{X}\mid \mathbf{Z})$ 中的 9 个因子相关联。

在形式上，因子图是有两种类型节点(因子节点、变量节点)的二分图 $F=(\mathcal{U},\mathcal{V},\mathcal{E})$(分别为(因子,变量,边))：因子节点(factor) ${\varphi }_i\in \mathcal{U}$ 和变量节点 (variable) ${\mathbf{x}}_j\in \mathcal{V}$，边 ${\mathbf{e}}_{ij}\in \mathcal{E}$ 总是存在于因子节点和变量节点之间。与因子 ${\varphi }_i$ 相邻的变量节点集合被写作 $\mathcal{N}\left({\varphi }_i\right)$，并且我们将对这个变量集合的赋值写为 ${\mathbf{X}}_i$ 。有了这些定义，我们就可以将因子图 $\mathbf{F}$ 定义为对作用于全体变量的函数 $\varphi (\mathbf{X})$ 的分解：
$$\varphi (\mathbf{X})=\prod _i{\varphi }_i\left({\mathbf{X}}_i\right)$$

换句话说，这些独立的关系由因子图中的边 ${\mathbf{e}}_{ij}$ 所编码，每一个因子都是一个在其邻接变量点集 $\mathcal{N}\left({\varphi }_i\right)$ 中变量 ${\mathbf{X}}_i$ 的函数。

每一个贝叶斯网络都可以简单地转换成一个因子图。因为贝叶斯网络中的每一个节点都指示了相应的变量及其父节点的一个条件概率密度，所以转换过程非常简单：每一个贝叶斯网络节点都分解为相应因子图中的一个变量节点和一个因子节点。因子与变量节点相连接，和贝叶斯网络中的父节点与对应的变量节点相连接的含义是一样的。如果贝叶斯网络中的一些节点是证据节点(evidence node)，即，它们所包含的变量是已知的，我们就忽略相应的变量节点：已知变量变成了相应的因子中的固定参数。

依照上述方法，在小型 SLAM 例子中，我们可以得到如下的因子图分解：
$$\begin{array}{rl}\varphi \left(l_1,l_2,x_1,x_2,x_3\right)& ={\varphi }_1\left(x_1\right){\varphi }_2\left(x_2,x_1\right){\varphi }_3\left(x_3,x_2\right)\\ & \times {\varphi }_4\left(l_1\right){\varphi }_5\left(l_2\right)\\ & \times {\varphi }_6\left(x_1\right)\\ & \times {\varphi }_7\left(x_1,l_1\right){\varphi }_8\left(x_2,l_1\right){\varphi }_9\left(x_3,l_2\right)\end{array}$$

我们可以很容易地看出因子和原始概率密度
$$\begin{array}{rl}p(\mathbf{X},\mathbf{Z})& =p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)\\ & \times p\left({\mathbf{l}}_1\right)p\left({\mathbf{l}}_2\right)\\ & \times p\left({\mathbf{z}}_1\mid {\mathbf{x}}_1\right)\\ & \times p\left({\mathbf{z}}_2\mid {\mathbf{x}}_1,{\mathbf{l}}_1\right)p\left({\mathbf{z}}_3\mid {\mathbf{x}}_2,{\mathbf{l}}_1\right)p\left({\mathbf{z}}_4\mid {\mathbf{x}}_3,l_2\right)\end{array}$$

或式
$$\begin{array}{rl}p(\mathbf{X}\mid \mathbf{Z})& \propto p\left({\mathbf{x}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_1\right)p\left({\mathbf{x}}_3\mid {\mathbf{x}}_2\right)\\ & \times p\left({\mathbf{l}}_1\right)p\left({\mathbf{l}}_2\right)\\ & \times l\left({\mathbf{x}}_1;{\mathbf{z}}_1\right)\\ & \times l\left({\mathbf{x}}_1,{\mathbf{l}}_1;{\mathbf{z}}_2\right)l\left({\mathbf{x}}_2,{\mathbf{l}}_1;{\mathbf{z}}_3\right)l\left({\mathbf{x}}_3,{\mathbf{l}}_2;{\mathbf{z}}_4\right)\end{array}$$

中的似然因子之间的对应关系。例如，${\varphi }_7\left({\mathbf{x}}_1,{\mathbf{l}}_1\right)=l\left({\mathbf{x}}_1,{\mathbf{l}}_1;z_2\right)\propto p\left(z_2\mid x_1,{\mathbf{l}}_1\right)$。

1.8 因子图支持的计算

在余下的篇幅中，我们把关注点放在 SLAM 的快速优化方法上，包括 因子图在通常意义上支持什么类型的计算。将一个贝叶斯网络 $p(X,Z)$ 转换为一个因子图（通过在证据观测 $\mathbf{Z}$ 上进行条件化）会生成一个后验概率的表示 $\varphi (X)\propto p(X\mid Z)$ 。那么，我们可以用它来做什么? 在 SLAM 领域，我们可以充 分利用因子的特殊形式来实现快速推断，也可以支持一些和具体领域无关的操作：评估、优化，以及采样。

给定任何一个定义了末归一化概率密度函数的因子图 $\varphi (X)$，我们可以通过简单地将每一个因子与结果相乘来对任何一个给定的值进行评估 (evaluate)。 因为评估中涉及的概率值通常较小，所以评估操作通常通过在对数或者反对数空间中对因子求和来完成，这样就可以得到数值稳定的解。评估提供了通往优化 (optimization) 的方法，几乎所有的不使用梯度的优化方法都可以直接使用。如果因子是连续变量的可微函数，那么基于梯度的方法可以迅速找到后验 概率的局部极大值。对于离散变量，可以使用图搜索方法，它们的时间花销通常会比较大。既涉及离散变量又涉及连续变量的问题是最难的。

我们最感兴趣的是后验概率的局部极大值或者全局最大值，而在一个概率密度分布函数中进行采样(sampling) 可以帮助我们进行可视化和计算与后验概率相关联的统计值和期望值。然而，1.5节中介绍的原始采样方法只适用于有向无环图。对于因子图有效的通用采样算法是马尔可夫链蒙特卡洛(Markov chain Monte Carlo)方法。其中的方法之一就是吉布斯采样 (Gibbs sampling)，方法为每一步从其条件概率密度分布中对单一变量进行采样，而条件概率密度分布由采样变量通过因子链接的所有其他变量所给定。这里我们假定了条件概率密度可以很容易地得到，然而，通常对于离散变量来说，条件概率密度都很难直接得到。