时间序列-异常检测（Anomaly Detection）（二）：传统方法

u013250861

已于 2023-10-27 23:08:30 修改

阅读量2k

点赞数

分类专栏：时间序列(Time Series) 文章标签：异常检测

于 2022-03-19 00:04:41 首次发布

本文链接：https://blog.csdn.net/u013250861/article/details/123587258

版权

时间序列(Time Series) 专栏收录该内容

20 篇文章

订阅专栏

一、基于统计的算法（具有分布假设）

1、针对单变量数据

1.1 集中不等式

集中不等式是数学中的一类不等式，描述了一个随机变量是否集中在某个取值附近

1.2 马尔可夫不等式

给出了一个实值随机变量取值大于等于某个特定数值的概率的上限。设X是一个随机变量，a>0为正实数，那么以下不等式成立：
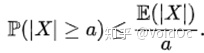
在这里插入图片描述

1.3 比切雪夫不等式

马尔可夫不等式给出了随机变量处于区间 [a,+inf] 概率的上限估计。切比雪夫不等式则给出了随机变量集中在距离其数学期望值距离不超过a的区间上之概率的上限估计：
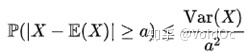
在这里插入图片描述

1.4 统计置信度检验

1.5 3-sigma

(μ−3σ,μ+3σ)区间内的概率为99.74。所以可以认为，当数据分布区间超过这个区间时，即可认为是异常数据。n-sigma异常检测准则：
在这里插入图片描述

1.6 t-检验，f-检验，卡方检验

检验一个正态分布的总体的均值是否在满足H0假设的值之内

1.7 Grubbs’ Test 和 ESD（Extreme Studentized Deviate test）

时间序列异常检测算法S-H-ESD - Treant - 博客园

1.8 ARIMA类

2、针对多变量数据

马氏距离：用来计算样本X与中心点μ的距离，也可以用来做异常分值，计算方式:
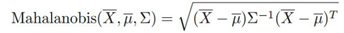
在这里插入图片描述
马氏距离最强大的地方是引入了数据之间的相关性（协方差矩阵）。而且马氏距离不需要任何参数，这对无监督学习来说无疑是一件很好的方法。通常一个简单的最近邻算法加上马氏距离就可以秒杀很多复杂的检测模型。

马氏距离+ KNN：DaiDongyang/knn
在这里插入图片描述

3、预处理

在这里插入图片描述

-对于纯随机序列，也称为白噪声序列，序列的各项之间没有任何的关系，序列在进行完全无序的随机波动，可以终止对该序列的分析。

-对于平稳非白噪声序列，它的均值和方差是常数。ARMA 模型是最常用的平稳序列拟合模型。

-对于非平稳序列，由于它的方差和均值不稳定，处理方法一般是将其转化成平稳序列。可以使用ARIMA 模型进行分析。

在这里插入图片描述

AR 是自回归， p 是自回归项， MA 是移动平均， q 为移动平均项， d 为时间序列称为平稳时所做的差分次数。

原理：将非平稳时间序列转换成平稳时间序列，然后将因变量仅对它的滞后值（p阶）以及随机误差项的现值和滞后值进行回顾所建立的模型。

在这里插入图片描述
实例：使用ARIMA 模型对某餐厅的销售数据进行预测

#coding=gbk
#使用ARIMA 模型对非平稳时间序列记性建模操作
#差分运算具有强大的确定性的信息提取能力， 许多非平稳的序列差分后显示出平稳序列的性质， 这是称这个非平稳序列为差分平稳序列。 
#对差分平稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。 
 
#导入数据
import pandas as pd
filename = r'D:\datasets\arima_data.xls'
data = pd.read_excel(filename, index_col = u'日期')
 
#画出时序图
import matplotlib.pyplot as plt     
plt.rcParams['font.sans-serif'] = ['SimHei']    #定义使其正常显示中文字体黑体
plt.rcParams['axes.unicode_minus'] = False      #用来正常显示表示负号
# data.plot()
# plt.show()

在这里插入图片描述

#画出自相关性图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# plot_acf(data)
# plt.show()
 
#平稳性检测
from statsmodels.tsa.stattools import adfuller
print('原始序列的检验结果为：',adfuller(data[u'销量']))
#原始序列的检验结果为： (1.8137710150945268, 0.9983759421514264, 10, 26, {'1%': -3.7112123008648155,
#  '10%': -2.6300945562130176, '5%': -2.981246804733728}, 299.46989866024177)
#返回值依次为：adf, pvalue p值， usedlag, nobs, critical values临界值 , icbest, regresults, resstore 
#adf 分别大于3中不同检验水平的3个临界值，单位检测统计量对应的p 值显著大于 0.05 ， 说明序列可以判定为 非平稳序列

在这里插入图片描述

#对数据进行差分后得到 自相关图和 偏相关图
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
 
D_data.plot()   #画出差分后的时序图
# plt.show()
 
plot_acf(D_data)    #画出自相关图
# plt.show()
plot_pacf(D_data)   #画出偏相关图
# plt.show()
print(u'差分序列的ADF 检验结果为： ', adfuller(D_data[u'销量差分']))   #平稳性检验
#差分序列的ADF 检验结果为：  (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': -3.6327426647230316, 
# '10%': -2.6130173469387756, '5%': -2.9485102040816327}, 287.5909090780334)
#一阶差分后的序列的时序图在均值附近比较平稳的波动， 自相关性有很强的短期相关性， 单位根检验 p值小于 0.05 ，所以说一阶差分后的序列是平稳序列

在这里插入图片描述

#对一阶差分后的序列做白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果：',acorr_ljungbox(D_data, lags= 1)) #返回统计量和 p 值
# 差分序列的白噪声检验结果： (array([11.30402222]), array([0.00077339])) p值为第二项， 远小于 0.05
 
#对模型进行定阶
from statsmodels.tsa.arima_model import ARIMA 
pmax = int(len(D_data) / 10)    #一般阶数不超过 length /10
qmax = int(len(D_data) / 10)
bic_matrix = []
for p in range(pmax +1):
    temp= []
    for q in range(qmax+1):
        try:
            temp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)
 
bic_matrix = pd.DataFrame(bic_matrix)   #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin()   #先使用stack 展平， 然后使用 idxmin 找出最小值的位置
print(u'BIC 最小的p值 和 q 值：%s,%s' %(p,q))  #  BIC 最小的p值 和 q 值：0,1
#所以可以建立ARIMA 模型，ARIMA(0,1,1)
model = ARIMA(data, (p,1,q)).fit()
model.summary2()        #生成一份模型报告
model.forecast(5)   #为未来5天进行预测，返回预测结果、标准误差和置信区间

利用模型向前预测的时期越长，预测的误差就会越大，这是时间预测的典型特点
在这里插入图片描述

二、基于相似度量的算法

1、基于距离度量

KNN：输入数据集D,参数k,n->对于每个点计算它的k邻近距离->按照距离降序排序->前N个点认为是离群点

2、基于密度度量

2.1 LOF（Local Outlier Factor）：局部离群因子检测方法，该算法会给数据集中的每个点计算一个离群因子

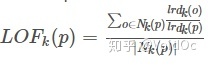
在这里插入图片描述
通过判断LOF是否接近于1来判定是否是离群因子。若LOF远大于1，则认为是离群因子，接近于1，则是正常点。

2.2、KDE 核密度估计

所谓核密度估计，就是采用平滑的峰值函数(“核”)来拟合观察到的数据点，从而对真实的概率分布曲线进行模拟：
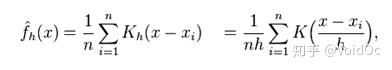
在这里插入图片描述
核密度函数的原理也比较简单，“核”是一个函数，用来提供权重。例如高斯函数 (Gaussian) 就是一个常用的核函数，如果某一个数在观察中出现了，我们可以认为这个数的概率密度很大，和这个数比较近的数的概率密度也会比较大，而那些离这个数远的数的概率密度会比较小。

3、基于聚类：K-means，GMM

缺点：聚类参数难界定，导致检测效果偏差；聚类训练开销较大

4、基于树：孤立森林（Isolation Forest）

iForest （Isolation Forest）孤立森林异常检测入门篇

基于集成学习（Ensemble），适用于连续数据的异常检测，通过多颗iTree形成森林来判定是否有异常点；这种方法很有效，但是并不总是有用的，比如说数据的分布不是沿着特征轴，而是随意分布，或者流型分布，就需要选择别的方式了。

iTree伪代码：
在这里插入图片描述
IF模型结构示意图：

在这里插入图片描述

5、基于谱（线性模型）：通过与正常谱型进行残差对比，发现异常

简单的线性模型就是相关性分析。利用一些自变量来预测因变量。比较重要的一个应用就是时序数据或者空间轨迹数据。我们可以利用上一个值或者上几个值来预测当前值，将预测值和实际值的误差作为优化对象，这样就建立了一个正常数据的模型，背离这个模型的就被当作异常值，预测值和实际值的误差也可以作为异常分值来提供

5.1 One-class SVM 矩阵分解法

（无监督，解决极度不平衡数据）

严格地讲，OneClassSVM不是一种异常点检测方法，而是一种奇异值检测方法，因为它的训练集不应该掺杂异常点（训练集只有一类），否则的话，可能在训练时影响边界的选取。但在数据维度很高，或者对相关数据分布没有任何假设的情况下，OneClassSVM也可以作为一种很好的outlier detection方法。