2025年数学SCI1区：混沌进化优化算法CEO，深度解析+性能实测

---

1.摘要

本文提出了一种基于种群的新型元启发式算法——混沌进化优化算法（Chaotic Evolution Optimization, CEO），其灵感源于二维离散忆阻器映射的混沌演化过程。CEO算法利用忆阻器映射的超混沌特性，通过数学建模引入随机搜索方向以驱动演化过程，并结合差分演化（Differential Evolution, DE）框架中的交叉和变异操作进一步优化算法性能。

2.领域背景

现实生活中的许多动态演化现象都表现出混沌特性，这种特性可用于揭示自然界的客观规律，并推动工业应用的快速发展。混沌行为的特点包括密集的周期轨道，以及初始敏感性、拓扑混合性和不可预测性等多种特性。当前的研究重点集中在构建多样化的混沌动力系统，以促进混沌在众多工业领域中的广泛应用。例如，研究人员利用混沌系统固有的随机性，开发了多种安全通信策略、元启发式算法以及物联网隐私保护系统。

随着动力学分析技术的深入发展和人工智能的进步，混沌退化现象逐渐被发现，混沌演化过程也能够被准确预测，这无疑给基于混沌的应用带来了巨大风险。因此，一种比混沌本身更为复杂的现象——超混沌（hyperchaos）引起了广泛关注。超混沌的特点是具有两个正的Lyapunov指数（LEs），实现超混沌的连续系统通常需要高维度和复杂的模拟电路，这与实际应用的需求不符。在离散映射中实现超混沌成为一条可行的路径，因为它仅需要两个维度，而连续动力系统至少需要四个维度。离散忆阻器超混沌映射开发高性能元启发式算法是一个新兴的研究领域，一个电荷控制的离散忆阻器模型：
$$\{\begin{array}{l}{\mathbf{v}}_t=\mathbf{M}({\mathbf{q}}_t){\mathbf{i}}_t,\\ q_{t+1}={\mathbf{q}}_t+{\mathbf{i}}_t,\end{array}$$

其中，$v_t$、$i_t$和$q_t$分别表示连续忆阻器中电压$v(t)$、电流$i(t)$和电荷$q(t)$在第$t$次迭代时的采样值。离散忆导电方程被特意选择为$M(q_t)=e^{-\cos \pi q_t}-1$,从而推导出指数型离散忆阻器。当电压$v_t$通过比例控制器$k$处理并作为延迟反馈输入时，可以得到一个统一的忆阻映射。本质上，通过将输出$v_t$和输入$i_t$分别替换为$x_{t+1}$和$x_t$,构建了一个指数型离散忆阻器 (EDM)映射，其形式为：
$$\{\begin{array}{llc}{x}_{t+1}=k\cdot (e^{-cos\pi y_t}-1)\cdot x_t& & \\ y_{t+1}=y_t+x_t& & \end{array}$$

3.算法原理

变异算子

CEO作为一种基于种群的进化算法，其变异算子采用统一的搜索框架：
$${\tilde{\mathbf{x}}}_{t+1}={\mathbf{x}}_t+a\cdot {\mathbf{d}}_t$$
其中，$x_t$和${\tilde{x}}_{t+1}$分别表示当前个体和变异个体；$a$表示搜索步长；$d_t$为演化方向，由动力学映射公式生成。
CEO 的核心思想是利用二维忆阻超混沌映射的超混沌特性，为种群提供演化方向：
$$\{\begin{array}{ll}{\mathbf{x}}_t^{{}^{\prime }}=\frac{{\mathbf{x}}_t-\mathbf{lb}}{\mathbf{ub}-\mathbf{lb}}-0.5& \\ & \\ {\mathbf{y}}_t^{{}^{\prime }}=\frac{{\mathbf{y}}_t-\mathbf{lb}}{\mathbf{ub}-\mathbf{lb}}\times 0.5-0.25& \end{array}$$

其中，$N$表示混沌样本的数量，可以生成$N$个混沌候选个体
x c h a o s = { x c h a o s l , … , x c h a o s N } x_{\mathrm{chaos}}=\{x_{\mathrm{chaosl}},\ldots,x_{\mathrm{chaos}N}\} xchaos​={xchaosl​,…,xchaosN​}和 y c h a o s = { y c h a o s 1 , … , y c h a o s N } y_{\mathrm{chaos}}=\{y_{\mathrm{chaos}1},\ldots,y_{\mathrm{chaos}N}\} ychaos​={ychaos1​,…,ychaosN​}。这些混沌个体可以通过逆映射，映射回优化问题的实际位置 x c h a o s ′ = { x c h a o s l ′ , … , x c h a o s N ′ } x_{\mathrm{chaos}}^{\prime}=\{x_{\mathrm{chaosl}}^{\prime},\ldots,x_{\mathrm{chaosN}}^{\prime}\} xchaos′​={xchaosl′​,…,xchaosN′​}和$y_{\mathrm{chaos}}^{\prime }=$ { y chaos 1 ′ , … , y chaos N ′ } \{y_{\text{chaos}1}^{\prime},\ldots,y_{\text{chaos}N}^{\prime}\} {ychaos1′​,…,ychaosN′​}。

映射公式为：
$$\{\begin{array}{c}{\mathbf{x}}_{-}{\mathbf{chaos}}^{n^{\prime }}=({\mathbf{x}}_{-}{\mathbf{chaos}}^n+0.5)\times (\mathbf{ub}-\mathbf{lb})+\mathbf{lb}\\ {\mathbf{y}}_{-}{\mathbf{chaos}}^{n^{\prime }}=({\mathbf{y}}_{-}{\mathbf{chaos}}^n+0.25)\times 2\times (\mathbf{ub}-\mathbf{lb})+\mathbf{lb}\end{array}$$

基于$x$和$y$可以分别为个体$x_i$和$y_i$生成$N$个演化方向：
$$\{\begin{array}{l}{\mathbf{d}}_{x,t}^n={\mathbf{x}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{x}}_t\\ {\mathbf{d}}_{y,t}^n={\mathbf{y}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{y}}_t\end{array}$$

CEO变异算子：
$$\{\begin{array}{ll}{\tilde{\mathbf{x}}}_{t+1}^n={\mathbf{x}}_t+a\cdot ({\mathbf{x}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{x}}_t)& \\ {\tilde{\mathbf{y}}}_{t+1}^n={\mathbf{y}}_t+a\cdot ({\mathbf{y}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{y}}_t)& \end{array}$$

为了进一步提高算法的局部发展能力，采用在当前种群中搜索最优解附近，加快算法的收敛速度：
$$\{\begin{array}{ll}{\tilde{\mathbf{x}}}_{t+1}^n={\mathbf{Best}}_t+a\cdot ({\mathbf{x}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{x}}_t)& \\ {\tilde{\mathbf{y}}}_{t+1}^n={\mathbf{Best}}_t+a\cdot ({\mathbf{y}}_{-}{\mathbf{chaos}}^{n^{\prime }}-{\mathbf{y}}_t)& \end{array}$$

选择算子

对于 $x_t$ 和 $y_t$，可以分别生成 $N$ 个试验向量 $x^{{\text{trial}}_h}$ 和 $y^{{\text{trial}}_h}$，CEO 采用贪婪准则来选择生成的实验向量：
$${\mathbf{x}}_{t+1}=\{\begin{array}{llc}{\mathbf{x}}_{-}{\mathbf{trial}}_t^{\ast },\mathrm{if}& f\left({\mathbf{x}}_{-}{\mathbf{trial}}_t^{\ast }\right)\le f({\mathbf{x}}_t)& \\ {\mathbf{x}}_t,& \mathrm{otherwise}& \end{array}$$

$${\mathbf{y}}_{t+1}=\{\begin{array}{ll}{\mathbf{y}}_{-}{\mathbf{trial}}_t^{\ast },\mathrm{if}f\left({\mathbf{y}}_{-}{\mathbf{trial}}_t^{\ast }\right)\le f({\mathbf{y}}_t)& \\ {\mathbf{y}}_t,\mathrm{otherwise}& \end{array}$$

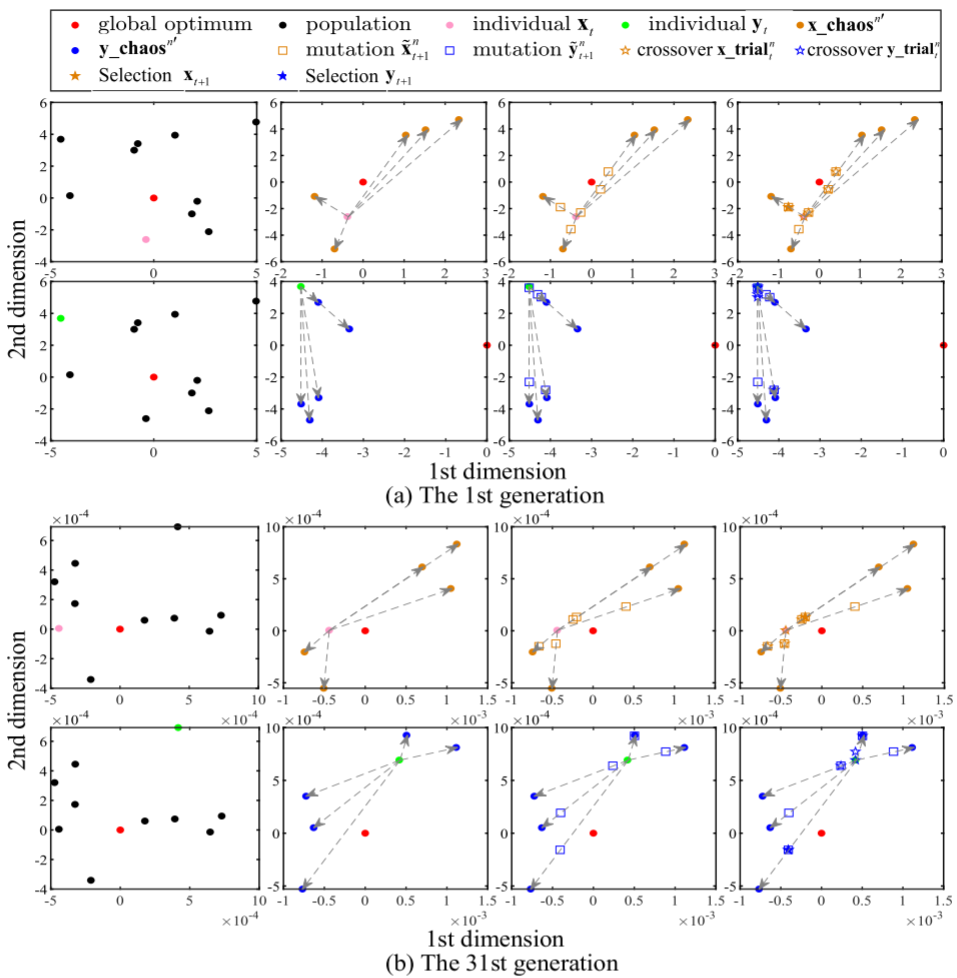
流程图

4.结果展示

5.参考文献

[1] Dong Y, Zhang S, Zhang H, et al. Chaotic evolution optimization: A novel metaheuristic algorithm inspired by chaotic dynamics[J]. Chaos, Solitons & Fractals, 2025, 192: 116049.

6.代码获取