一、说明
本篇叙述中心射影、透视射影的概念,其实中心射影就是透视射影的特殊情形。为了铺垫以后的三点论和四点论,的概念准备:
- 射影映射(变换)前后,共线三点依然共线
- 射影映射(变换)前后,共线四点的交比不变
二、中心射影
2.1 直线上的中心射影

注意:以上有几个特殊映射点
1)ξ , η平行时,认为其无穷远处相交,因而和过O的平行线也在无穷远处相交。无穷远点是个特殊点。(严格来说,无穷远点也有两个,但重合了)。
2)当ξ , η相交时,Q点是ξ上无穷远点在的η映射;P点是η上无穷远点的在ξ的映射。
3)当ξ , η相交时,交点D是两条直线的自映射点,即原像和映像重合。
4)考虑无穷远点是此类几何的必选项。
2.2 平面上的中心射影
定义:对于平面和
,O是两个平面外的点,O引出的射线
交
和
于
和
,
和
上的对应关系就是平面
和
上的中心射影。
叫射影线,
是原像,
是像点,平面
和
的交线s上的点是自对应点。

在平面上的
线上点,投影到
后,与
线对应,因此,原像的ABC共线,射影后,
依然共线。
三、透视映射
定义1: 线束与不通过中心S的直线s相交,得一点列s(A,B,C......)
,则点列s(A,B,C......)叫做线束在直线s上的截影,如图3所示 。

一句话概括:通过线束生成直线。
定义2 点列s(A,B,C......)的点与不在底s上一点S连接,得一线束,则线束
叫做由点S投射到s(A,B,C......)的线束。
一句话:通过直线生成线束。
定义3 如果点列s(A,B,C......)是线束在直线s上的截影,那么这个截影叫做从线束
到点列s(A,B,C......)一个透视对应。
直线和线束构成的映射就是透视映射。说到头,透视映射就是中心映射。然而,它关注的不是像点与原像点的对应。而是投射线与原像点(这里没有第二条线,所以不谈像点)的对应。这种对应关系是对偶的。
定义4 如果两个点列与同一个线束成透视对应,那么这两个点列叫做透视点列,线束中心叫做透视中心,两点列中同在线束的一条直线上的两点叫做对应点。

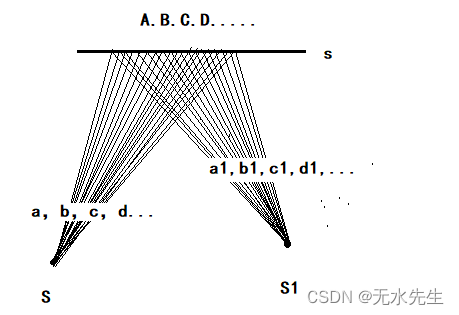
如图5所示,线束分别在直线s和s'上的截影s(A,B,C......)与s'(A',B',C.'.....)成透视点列.
定义5 如果两个线束与同一点列成透视对应,那么这两个线束叫做透视线束,点列的底叫做透视轴,两线束中交于透视轴上同一点的一对直线叫做对应直线。

如图6所示,由点S,S'分别投射到点列s(A,B,C......)所得的两个线束与
成透视线束.
由上讨论可知,两个成透视对应的点列,其中对应点的连线必共点;两个成透视对应的线束,其对应线的交点必共线。

四、重要结论
- 1 中心射影就是透视射影。但两者立场有高低。
- 2 二两者不同在于,中心射影站在个别点线立场上分析,透视射影站在集合(线束)和点列立场上分析。
- 3 中心射影中:对偶要素是【点,线】,透视射影中,对偶要素是【线束,点列】








 本文深入讲解中心射影和透视射影的数学概念,强调它们在几何学中的特殊情形和共通点。中心射影包括直线和面上的射影,透视射影关注线束和点列的对应。两者的核心区别在于分析视角,中心射影侧重个体点线,而透视射影聚焦于集合和线束。通过对偶性的讨论,揭示两者之间的内在联系。
本文深入讲解中心射影和透视射影的数学概念,强调它们在几何学中的特殊情形和共通点。中心射影包括直线和面上的射影,透视射影关注线束和点列的对应。两者的核心区别在于分析视角,中心射影侧重个体点线,而透视射影聚焦于集合和线束。通过对偶性的讨论,揭示两者之间的内在联系。


















 5917
5917

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










