【射影几何09】交比定律和迪萨格定律

无水先生

已于 2024-05-25 22:49:54 修改

阅读量4.2k

点赞数 21

分类专栏： # 射影几何和slam基础文章标签：机器学习人工智能

于 2024-01-18 05:49:25 首次发布

本文链接：https://blog.csdn.net/gongdiwudu/article/details/135634296

版权

射影几何和slam基础专栏收录该内容

19 篇文章

订阅专栏

本文探讨了射影几何中交比的概念，从定比分点出发，通过证明交比的射影不变性，展示了迪萨格定律的证明过程。文章揭示了交比在圆锥曲线中的应用，强调了交比在实际问题中的发现和运用策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、说明

在射影几何中，映射不能保证线段长度一致，映射不能保证平行关系一致，映射不能角度的一致，也不能保证线段的比例关系一致，然而，能保证直线的一致，同时发现“交比”的一致性。进而，发现迪萨格定律。本文将围绕“交比”这个概念展开讨论。

二、概念演进

2.1 从定比分点说起

定义：对于P1，P2决定的有向直线L上，存在分点P，那么，P将P1P2分成两个部分，P1P和PP2，因此存在分点定比λ。

$\lambda =\frac{P1P}{PP2}$

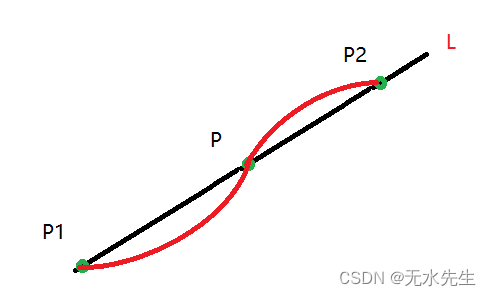
当P在P1P2的外侧，则λ为负值，下图用红色标注正方向，蓝色标注反方向，如图：

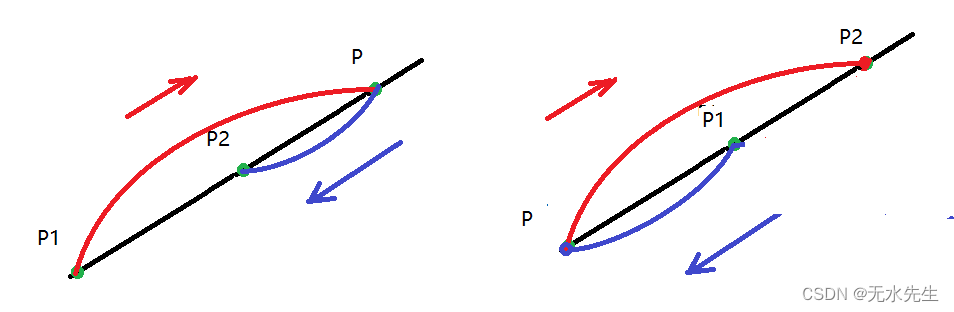
强烈提示：直线P1P2是有方向的！！不要忽视这个规定。

2.1 两个定比分点引出交比概念

将定比分点定义成两个，对于P1P2两点构成的直线L上，定义两个分点Q1和Q2，所以：

$\lambda_1 =\frac{P1Q1}{Q1P2}$

$\lambda_2 =\frac{P1Q2}{Q2P2}$

交比的定义：

$(P1,P2; Q1,Q2)=\frac{\lambda_1}{\lambda_2} =\frac{ \frac{P1Q1}{Q1P2}}{\frac{P1Q2}{Q2P2}}= \frac{P1Q1*Q2P2}{Q1P2*P1Q2}$

一般地，对于极点为P的射影线，横穿直线L1,和L2，如下图：

那么，将A、B视为基点，AB构成原始有向直线段，C和D是两个分点，交比表示为：

$(A,B; C,D) = \frac{AC}{CB} * \frac{DB}{AD}$

在交比中，四个点是成对出现的。我们将其称之为两个点对（或者点偶）。

定理（交比的射影不变性）如图所示，过点P引四条相交直线构成射影线束，分别与另外两条直线交于A,B,C,D和A‘,B’,C‘,D’，则（A’，B'；C‘，D’)=(A，B；C，D).即射影投影下，直线上被射影线束所分割的线段，这些线段的交比不变。

这种交比之所以不变，是因为从P发出的各条射线角度固定引起的，下面我们证明这种交比只和发射线束之间的角度有关系，因为发射角度不变，交比也不变。

三、交比射影不变性的证明。

3.1 定理描述

如下图：我们考察线l1和P的线束的焦点，试图得到：

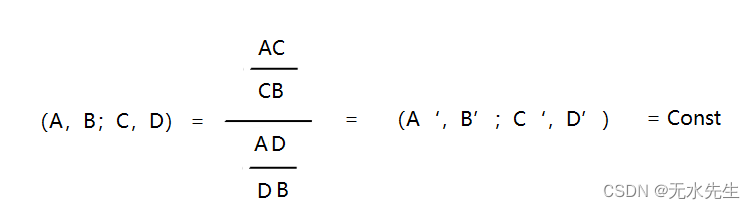
它们构成若干三角形，我们这里从面积上考虑之。

3.2 从三角形面积入手

设射影中心到直线l1的距离为h。于是三角形PAC的面积可以用两种方式加以表达：

上述通过同一个三角形两种表达，就导致用两个侧边、高，表示出底边。注意，这里高h是几个三角形共同拥有的。

同理得到：

带入公式（1）

这说明，用任意直线被一组四条共点直线形成的线束（下文均简称为“线束”）切割，得到的四个点的交比的绝对值是一个定值。根据我们上面的推导，这个定值仅与四条直线之间的夹角相关。

可以看到，交比实际上是各个射影角度构成的表达式，与被切割直线摆放位置，或被切的线段长度无关。

四、德萨格定律和证明

4.1 用交比的概念证明迪沙格定理。两个三角形对应顶点连线交于一点（三线共点），则对应边交点位于一条直线上（三点共线）。如下图所示，AA'、BB'和CC'共点（点P），则AB与A'B'的交点X，BC与B'C'的交点Y，CA与C'A'的交点Z，证明X，Y，Z三点在一条直线上。

分析：这里显然，X点和Y点能够连成一条直线，至于Z是不是在XY线上，正是我们需要说明的地方。基本思路是，通过X为极点的线束构成一个透视，通过Y为极点的线束构成一个透视，那么同样地，通过Z的线束也构成一个透视映射，这个Z点能落在XY连线上，就可以完成证明。

连接XY，这时我们还不能确定点Z是否位于XY上，我们下面就是要证明点Z确实在XY上。设XY与PA'、PB'、PC'的交点分别为E、D、F。连接XP，连接YP，连接ZP。如下图所示。

考虑从X发出的线束XP、XA、XE、XA'。它们都与直线PA'和PB'相交。交点分别是：P、A、E、A'和P、B 、D、B'。因而构成一个透视映射，由交比的不变性，得：

( PA；EA' ) = ( PB；DB' )

类似地，考虑Y发出的线束YP、YB、YD、YB'。它们与直线PB'和PC'相交。交点分别是：P、B、D、B'和P、C、F、C'。由交比的不变性，得：

( PB；DB' ) = ( PC；FC' )

由以上两个交比的等式，得到：

( PA；EA' ) = ( PC；FC' )

因此。（P，A，E，A'）和 ( P，C，F，C' )将出自一个透视映射S，且S的线束为：

SP，SAC, SEF, SA'C', 于是，AC、EF、A'C'三线相交于一点S.

由于已知AC和A'C'相交于Z，因为只有一个交点，因此，S和Z点重合；因而EF必须经过点Z，即点Z位于直线XY上。所以，我们最终证明了X、Y、Z三点共线。

五、交比的线模式表示

交比这个概念在圆锥曲线上发挥作用，这里不得不说，其作用的原理。我们先回到交比的定义上来，如下图：

交比是: $(A,B;C,D)=\frac{AC}{BC}:\frac{AD}{BD}=\frac{sin\angle APC}{sin\angle BPD}:\frac{sin\angle APD}{sin\angle BPD}$

这里用两条射线表示一个夹角，于是，引出交比的线束表示：

$(PA,PB,PC,PD)=\frac{sin[PA,PC]}{sin[PC,PB]}\frac{sin[PA,PD]}{sin[PD,PB]}=(A,B;C,D)$

其中：sin[PA,PC] 等价于 $sin \angle A PC$ ；这里看起来并没有太多差别，不过放到圆锥曲线中，你就看出这个定义的非凡之处。

从上图的表达中，我们能够看到（A，B；C，D）=（A'，B'；C'，D'）这似乎并不稀奇，那么更多的发现是什么呢？

是不是有如下等价说法？：

$(A,B;C,D) =\frac{AF}{EF}:\frac{A'D'}{D'E}$

是不是说：交比关系可以传递到圆内接四边形A'EFD'中呢？或者反过来，圆内接四边形与某个射影交比有关呢？

六、结论

在实际应用中，并不是去计算交比，而是发现构成交比的现场场景--即四线束射影投射到直线上。从上文我们对迪萨格定理证明中不难发觉，其巧妙点在于，发现X点构成透视射影，Y点构成透视射影；通过交比传递性，能够说明，Z点也是个透视射影，从而证明XYZ的共线性。

其它基础知识：梅塞定理/反演/调和/蒙日定理/布洛卡定理/交比/彭塞列小定理/笛萨格定理/帕普斯定理/帕斯卡定理/布利安桑定理/坎迪定理/牛顿定理