ML 系列：第 27 节 - 连续概率分布（Gamma分布）

最新推荐文章于 2025-03-09 11:52:15 发布

无水先生

最新推荐文章于 2025-03-09 11:52:15 发布

阅读量1.8k

点赞数 33

分类专栏：概率模型机器学习专栏文章标签：概率论

本文链接：https://blog.csdn.net/gongdiwudu/article/details/143956106

版权

机器学习专栏同时被 2 个专栏收录

101 篇文章

订阅专栏

概率模型

14 篇文章

订阅专栏

一、说明

二、什么是 Gamma 分布？

2.1 为什么 Gamma 分布在机器学习中很重要？

一、说明

在这篇博文（第 27 节）中，我们将探讨Gamma 分布，这是一种用途广泛且应用广泛的连续概率分布。了解 Gamma 分布对于贝叶斯统计至关重要。这篇文章将介绍数学定义、关键属性、实际应用以及如何使用 Python 实现和可视化 Gamma 分布。

之前，我们讨论了均匀分布和高斯分布，它们为连续概率分布奠定了基础。现在，我们将在此基础上深入研究 Gamma 分布，并探索其独特的特性和用途。

二、什么是 Gamma 分布？

Gamma 分布是一种连续概率分布，它模拟泊松过程中α (alpha)事件发生的时间，其中α 是形状参数。它对于模拟偏斜分布特别有用，由两个参数定义：形状参数( α )和速率参数 ( β )。

2.1 为什么 Gamma 分布在机器学习中很重要？

能够对正值数据进行建模：Gamma 分布非常适合表示不能为负的变量，这使得它对于对机器学习任务中的响应时间或计数等数量进行建模很有用。
处理可变性和偏斜性：凭借其形状和尺度参数，Gamma 分布可以有效捕捉数据分布中不同程度的偏斜度和形状，从而实现对各种数据集的准确建模。
在贝叶斯推理中的重要性：作为某些似然函数的共轭先验，Gamma 分布简化了贝叶斯参数估计和概率建模，提高了贝叶斯机器学习算法的效率和准确性。

2.2 Gamma 分布的数学定义

为了充分理解 Gamma 分布，我们需要深入研究其数学公式。本节将介绍概率密度函数 (PDF)、关键参数和相关数学概念。

2.3 概率密度函数 (PDF)

Gamma 分布的概率密度函数 (PDF) 定义为：

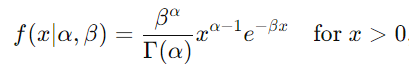
在哪里：

α > 0 是形状参数，
β > 0 是速率参数，
Γ(α) 或 (Gamma(alpha) 是 Gamma 函数，它将阶乘函数推广到连续值。

Gamma 函数 Γ(α) 定义为：

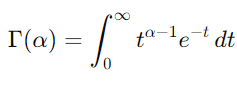
对于α的整数值，Gamma 函数简化为：

2.4 关键参数

形状参数（α）：

控制分布的形状。
当 α = 1 时，Gamma 分布简化为指数分布。

速率参数（β）：

与尺度参数 (θ) 成反比，其中 θ = 1/β。
控制事件发生的速率。

2.5 均值、方差和众数

Gamma 分布具有以下属性：

平均值（μ）：

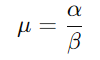
方差（σ2）：

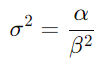
模式：

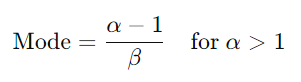
三、Gamma 分布与其他分布的关系

Gamma 分布用途广泛，与其他几个重要的概率分布有联系。了解这些关系可以更深入地了解各种分布的运作方式和应用方式。在这里，我们将详细探讨这些关系，包括展示这些联系的具体公式。

3.1 指数分布

Gamma 分布公式：

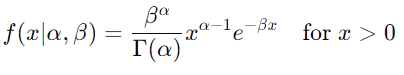
当形状参数 α=1 时，Gamma 分布简化为指数分布。指数分布通常用于对泊松过程中事件之间的时间进行建模。

指数分布公式：

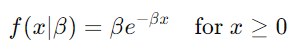
要从Gamma 分布转换为指数分布：

设置 α = 1
该公式简化为：

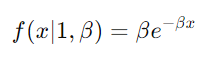
3.2.卡方分布

卡方分布是 Gamma 分布的一个特例，具有特定的参数值。它广泛应用于统计推断，特别是假设检验和构建置信区间。

Gamma 分布公式：

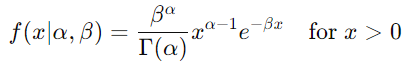
对于卡方分布，形状参数α 为 k/2，速率参数β 为 1/2，其中 k 是自由度。

卡方分布公式：

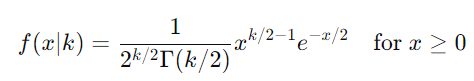
要从 Gamma 分布转换为卡方分布：

设 α = k/2
设置 β = 1/2
公式变为：

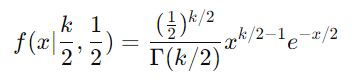
3.3. Erlang 分布

埃尔朗分布是伽马分布的一个特例，其中形状参数 α 是正整数。它在排队理论和电信中用于模拟等待时间。

Gamma 分布公式：

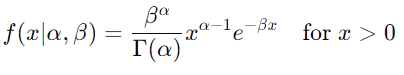
对于 Erlang 分布，α=k（一个整数），β 是速率参数。

埃尔朗分布公式：

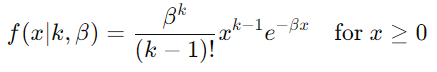
要从 Gamma 分布转换为 Erlang 分布：

设定 α = k （其中 k 是整数）
公式变为：

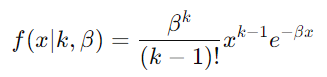
3.4. Beta 分布

Beta 分布与 Gamma 分布相关，因为它使用 Gamma 随机变量构造 Beta 随机变量。具体来说，如果 X 和 Y 是独立的 Gamma 分布随机变量，分别具有参数 (α1, β) 和 (α2,β)，则随机变量 (Z = X / X + Y) 服从 Beta 分布。

Gamma 分布公式：

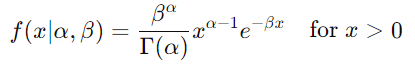
Beta 分布公式：

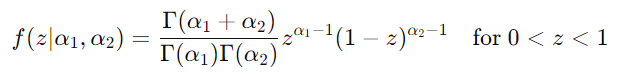
要从 Gamma 分布导出 Beta 分布：

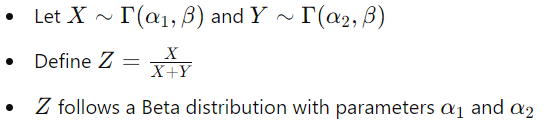
3.5. 逆伽马分布

逆伽马分布是伽马分布随机变量的倒数分布。如果 X∼Γ(α,β)，则 Y=1/X 服从逆伽马分布。

Gamma 分布公式：

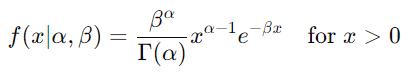
逆伽马分布公式：

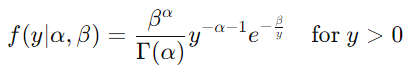
要从 Gamma 分布导出逆 Gamma 分布：

令 X∼Γ(α,β)
定义 Y=1/X
Y 服从参数为 α 和 β 的逆伽马分布

四、示例和python计算

4.1 Gamma 分布示例

假设我们有一个 Gamma 分布，其中 α=3 和 β=2。

意思是：

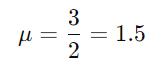
差异：

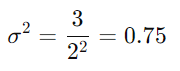
众数（因为 α > 1）：

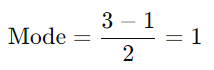
4.2 Python 实现

提供 Python 代码以从 Gamma 分布生成随机样本。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
alpha = 2.0
beta = 1.0

# Generate samples
samples = np.random.gamma(alpha, 1/beta, 1000)

# Plot the histogram
plt.hist(samples, bins=30, density=True, alpha=0.6, color='g')

# Plot the PDF
from scipy.stats import gamma
x = np.linspace(0, np.max(samples), 1000)
pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, pdf, 'k', linewidth=2)
plt.title('Gamma Distribution (alpha = {}, beta = {})'.format(alpha, beta))
plt.xlabel('x')
plt.ylabel('Density')
plt.show()

这是上述代码的输出：

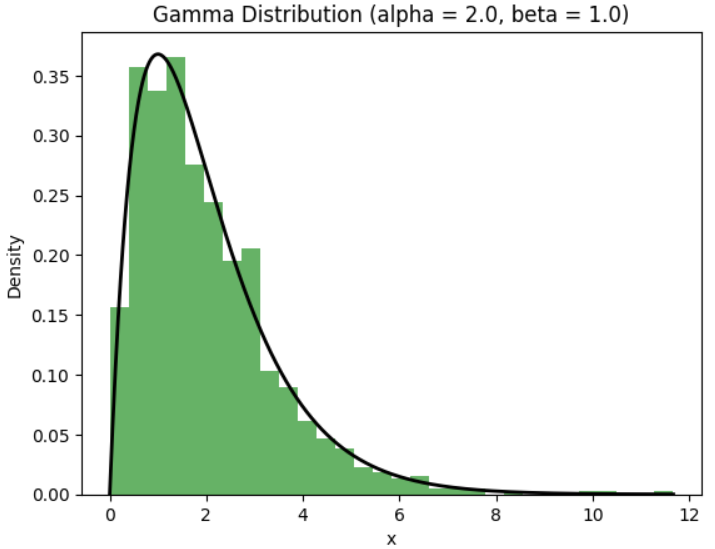
图 1.从 Gamma 分布生成随机样本

4.3 Gamma 分布的参数估计

从数据中估计 Gamma 分布的参数是统计建模中的一项关键任务。在本节中，我们将讨论如何使用最大似然估计 (MLE) 方法估计形状参数 (α) 和速率参数 (β) 。MLE是一种广泛使用的方法，用于通过最大化似然函数来估计统计模型的参数。

我们可以使用优化技术在 Python 中实现 MLE 方法来找到最大化对数似然函数的参数α和β。以下是使用该函数的代码示例scipy.optimize.minimize：

from scipy.optimize import minimize
from scipy.special import gamma, digamma

def negative_log_likelihood(params, data):
    alpha, beta = params[0], params[1]
    n = len(data)
    log_likelihood = n * (alpha * np.log(beta) - np.log(gamma(alpha))) + (alpha - 1) * np.sum(np.log(data)) - beta * np.sum(data)
    return -log_likelihood

# Generate sample data
data = np.random.gamma(alpha, 1/beta, 1000)

# Initial guesses for alpha and beta
initial_params = [1.0, 1.0]

# Minimize the negative log-likelihood
result = minimize(negative_log_likelihood, initial_params, args=(data,), bounds=[(1e-5, None), (1e-5, None)])
estimated_alpha, estimated_beta = result.x
print(f"Estimated alpha: {estimated_alpha:.3}")
print(f"Estimated beta:  {estimated_beta:.3}")