【流体力学01】：连续性方程

无水先生

已于 2024-08-26 19:22:04 修改

阅读量2.5w

点赞数 6

分类专栏：基础理论文章标签：算法数学模型

于 2021-12-17 16:15:51 首次发布

本文链接：https://blog.csdn.net/gongdiwudu/article/details/121991309

版权

基础理论专栏收录该内容

52 篇文章

订阅专栏

本文介绍了流体力学中的连续性方程，详细探讨了质量守恒原理，并通过具体实例解释了贝努力方程及其适用条件。此外，还讲解了流线与流管的概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

关键词：

continuity equation

一、守恒量方程

在物理学里，连续性方程（continuity equation）乃是描述守恒量传输行为的偏微分方程。由于在各自适当条件下，质量、能量、动量、电荷等等，都是守恒量，很多种传输行为都可以用连续性方程来描述。

连续性方程乃是微小区域的守恒定律方程。与全域性的守恒定律相比，这种守恒定律比较强势。在本条目内的所有关于连续性方程的范例都表达同样的要点──在任意区域内某种守恒量总量的改变，等于从边界进入或离去的数量；守恒量不能够增加或减少，只能够从某一个位置迁移到另外一个位置。

每一种连续性方程都可以以积分形式表达（使用通量积分），描述任意有限区域内的守恒量；也可以以微分形式表达（使用散度算符），描述任意位置的守恒量。应用散度定理，可以从微分形式推导出积分形式，反之亦然。

二、质量守恒

在流场中考虑一固定体积 $\Omega$ ，流体有从 $\Omega$ 的表面流入，也有流出。这里，流入和流出都按流出计量，那么流入就是负流出量。

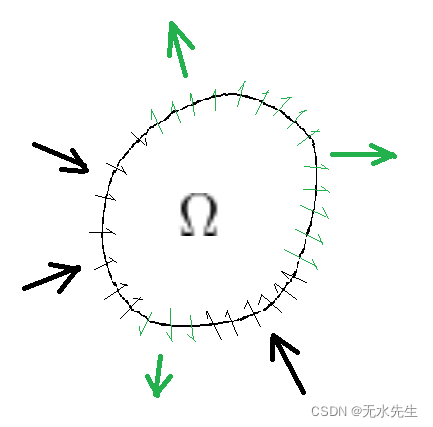
微面积、体积和微质量：

如图，面积微元是ds，流体速度为u，微体积是 $u\cdot ds$ ，微质量为： $\rho uds$ ， $\rho$ 是密度。

单位时间流出该体积的质量为以下封闭面积分：

$\oint \rho u\cdot ds$ （流入、流出都计为流出）

单位时间该体积内质量的减少为：

$- \frac{\partial }{\partial t}\int \rho dV$

因为质量不能凭空多出，因此两者是相等的：

$\oint \rho u\cdot ds = - \frac{\partial }{\partial t}\int \rho dV$

$\oint \rho u\cdot ds +\frac{\partial }{\partial t}\int \rho dV = 0$

将封闭面的积分转换成对体的积分，有：

$\int \bigtriangledown \cdot (\rho u)dV + \frac{\partial }{\partial t}\int \rho dV = 0$

消去 $dV$ 后，形成如下方程：

$\bigtriangledown \cdot (\rho u) + \frac{\partial \rho }{\partial t} = 0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; 1.1$

此方程的定性解释是：总量减少对时间归一 = 动量分量与速度乘积的总和。

流体的连续性方程是基于质量守恒推导得来，因此方程(1.1)适用于任意流场。

三、贝努力方程

3.1 贝努力方程的推导

贝努力方程是液体流体方程，条件是：

1）流体不可压缩
2）流体定长状态

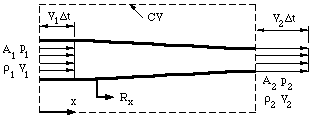
当流体运动时，它的运动方式必须保证质量守恒。要了解质量守恒如何对速度场施加限制，请考虑流体通过管道的稳定流动（即入口和出口流量不随时间变化）。流入和流出是 一维的，因此速度 V 和密度 ρ 在区域 A 上是恒定的（图 14）。

图 14. 显示控制体积的一维管道。

现在我们应用质量守恒定律。由于没有流过管道侧壁的流量，因此通过 A_1 进入的质量会从 A_2 流出（流量稳定，因此不会出现质量累积）。在很短的时间间隔Δt内，

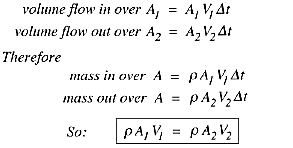
这是对具有一个入口和一个出口的稳定、一维流的质量守恒原理的陈述。该方程称为稳定一维流的连续性方程。对于通过具有多个入口和出口的控制体积的稳定流量，净质量流量必须为零，其中流入为负，流出为正。

3.2 流线和流管

流线是与瞬时速度方向相切的线（速度是矢量，有大小和方向）。为了在流动中形象化这一点，我们可以想象一个小的标记流体元素的运动。例如，我们可以用荧光染料标记一滴水，然后用激光照射它，使其发出荧光。如果我们在水滴根据局部速度场移动时拍摄一张短曝光照片（与速度明显变化所需的时间相比，曝光需要很短），我们会看到一条短条纹，长度为 V \Delta t，方向与瞬时速度方向相切。如果我们用这种方式标记许多水滴，水流中的流线就会变得可见。由于流动中任意一点的速度具有单一值（流动不能同时沿多个方向流动），因此流线不能交叉。速度大小为零的点除外，例如驻点。

还有其他方法可以使流程可见。例如，我们可以使用长曝光照片描绘出荧光滴所遵循的路径。这条线称为 路径线，它类似于您在夜间拍摄高速公路上的车灯长时间曝光照片时看到的东西。路径是可能交叉的，正如您可以从高速公路的类比中想象的那样：当汽车改变车道时，其灯光描绘出的路径可能会与相邻车辆在不同时间描绘出的另一条路径相交。

另一种可视化流动模式的方法是使用条纹。条纹是由在某个较早时间经过特定点的所有粒子所描绘的线。例如，如果我们从固定点连续发出荧光染料，染料在经过下游时会形成一条条纹。继续高速公路的类比，它是由经过同一收费站的所有车辆上的灯组成的线。如果它们都遵循相同的路径（稳定流），则会产生一条线，但如果它们遵循不同的路径（不稳定流），则该线可能会与自身交叉。在非定常流中，流线、路径线和条纹线都不同，但在稳定流中，流线、路径线和条纹线是相同的。