机器人学之动力学笔记【11】—— 拉格朗日 动力学方程
1. 拉格朗日法
之前我们学习了如何使用牛顿-欧拉法(基于力和力矩分析)建立机械臂的动力学方程,这一节要学习拉格朗日法(基于能量分析)建立机械臂的动力学方程。

动能
每一个杆件的动能 = 移动动能 + 转动动能
整个系统动能 = 所有杆件动能之和
动能是角度和角速度的函数,写成通用矩阵式

势能
每个杆件的势能 = 每个杆件的重力势能 + 零势能点
整个系统势能 = 所有杆件势能之和
势能是角度的函数

定义 Lagrangian 表达式

定义运动方程表达式:Lagrangian 对 θ(dot) 求偏导后求微分 - Lagrangian 对 θ 求偏导
展开后就是第二个式子
2. 举例:An RP Manipulator
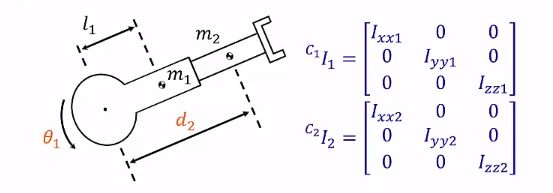
第一个杆件的速度 ,则移动动能 =
,则移动动能 = 

第二个杆的移动动能要注意,一个分量是由 造成的,另一个分量是由
造成的,另一个分量是由 造成的,所以移动动能是
造成的,所以移动动能是


有了动能有了位能之后,直接代入拆解后的各个部分计算

整理出来

利用 State-Space representation 拆开理解

3. 转换到笛卡尔空间下
我们写出来的动力学方程是 joint space 下的方程式,也就是我们知道了每个手臂关节的状态
 就可以知道达成这个运动状态所需要的关节的扭力是多少。
就可以知道达成这个运动状态所需要的关节的扭力是多少。
在笛卡尔空间下面,在看末端点的加速度状态的时候,末端点的加速度和力的关系是什么?那现在就可以使用之前学习过的雅克比矩阵把本来的方程式转换到笛卡尔空间下面的运动方程式

之前学过,joint torque 和 end effector 的 force 之间存在一个雅克比矩阵

整理出来得到上式,再拆解开来。
重新回看之前双旋转自由度机械臂的例子,之前是用牛顿-欧拉法去做,并且找到了一下三个矩阵

我们现在想做的事是把它换到笛卡尔空间下面,在机器人学之运动学笔记【8】—— 微分运动学中我们已经得到了雅克比矩阵 J(θ) ,所以它的逆矩阵和导数如下:

然后就是代公式,找到这个机械臂在笛卡尔空间下面的表达法:

像之前一样将科式力和离心力也拆解出来,拆解的更彻底一点

代入求解:

4. 考虑能量损耗

注意:
我们在推导拉格朗日方程的时候认为力做的功都转换为了动能和势能,过程中没有损耗。但是在实际机械臂中,没有摩擦是不可能的。这里引入阻尼力损耗的概念,那另外一个就是库仑摩擦,基本上是一个定值,但是它在静止时和运动时是不一样的,分为静摩擦和动摩擦








 本文介绍用拉格朗日法(基于能量分析)建立机械臂动力学方程,包括动能、势能及Lagrangian表达式的定义。通过An RP Manipulator举例计算,还将动力学方程从关节空间转换到笛卡尔空间,最后考虑实际中机械臂存在的能量损耗,如阻尼力损耗和库仑摩擦。
本文介绍用拉格朗日法(基于能量分析)建立机械臂动力学方程,包括动能、势能及Lagrangian表达式的定义。通过An RP Manipulator举例计算,还将动力学方程从关节空间转换到笛卡尔空间,最后考虑实际中机械臂存在的能量损耗,如阻尼力损耗和库仑摩擦。
















 632
632

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








