组合导航系列文章（十二）：滤波器基本原理

我觉得不错的地方

3. 滤波器估计原理

组合导航中，先验是imu解算的值，观测是gps等传感器给出的值，融合的目的是找到概率最大的那个值。上面介绍的三种方法都是对先验和观测的融合，由于极大似然要求先验为平均分布，而组合导航中，先验和观测都假设为高斯，导致只能用最大后验估计和贝叶斯估计，又由于贝叶斯估计要求观测的全概率（即上面贝叶斯公式里的P(X)），带来了很大的复杂性，因此往往都是使用最大后验估计。Kalman就是最大后验的一种典型实现形式，当然，在线性高斯情况下它和贝叶斯估计是等价的，使用贝叶斯方法同样能推导出kalman，只是在非线性情况下二者不再等价。

 

这篇文章的作者也是深蓝学院《多传感器融合定位》这个课的老师

摘自：https://zhuanlan.zhihu.com/p/150367249

组合导航系列文章（十二）：滤波器基本原理

任乾

保持谦虚的态度，世界是一面镜子

《组合导航系列文章》是《从零开始做自动驾驶定位》系列的第二阶段，从本阶段开始，文章在《泡泡机器人》公众号上首发，知乎用来备份和以后可能出现的必要更正。

泡泡机器人文章链接：组合导航系列文章（十二）：滤波器基本原理

 

以下是原文：

1. 概述

滤波器是组合导航的核心，是把惯性导航的解算结果和其他传感器输出的观测结果连接在一起的纽带，只有借助它，才能使二者优势互补，得到一个精确、稳定的导航系统。组合导航中使用的滤波器有很多，常见的有卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)、迭代扩展卡尔曼滤波(IEKF)、无迹卡尔曼滤波(UKF)、粒子滤波(PF)，本篇文章会一一介绍他们的原理，只是在这之前，我们需要回忆一下以前学过的一些参数估计的基础知识。

2. 参数估计思想

理解参数估计思想，重点要区分的是三个方法：极大似然估计、最大后验估计、贝叶斯估计。

 

4. 滤波器改进

以上所有的推导都是在线性高斯假设下进行的，当传递函数为非线性时，这个更新过程便无法进行。这里给出《概率机器人》里面的一张图，对比说明线性和非线性之间的差异。

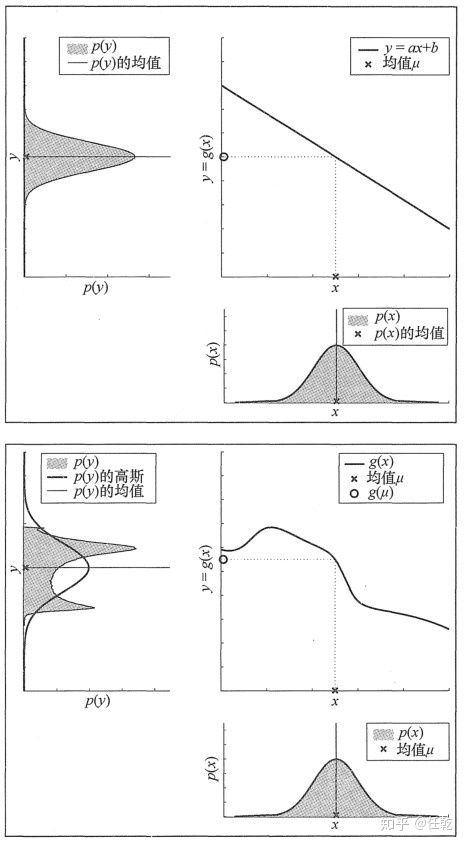
除了经典kalman以外，其他kalman的改进形式基本都是为了解决这个问题。主要包括这样几种：

1) 扩展kalman(EKF)

面对非线性问题，EKF采用了一种最简单的解决办法，就是把非线性近似成线性，采用的是泰勒展开的方法。由于这种线性只是近似出来的，它的结果自然是有偏的，而且泰勒展开的点是当前估计值，即便是在滤波收敛之前，估计值和真值还有很大差异，它仍然只能采用这种不准确的值去近似。这就造成了一个问题，如果状态模型收敛性很好，就可以形成一个良性循环“当前值处泰勒展开->估计得到更精确值->更精确值处展开->估计进一步精确”，但是如果收敛性不好，状态量的波动比较大，那么良性循环则可能变成恶性循环，导致滤波器发散。

2) 迭代扩展kalman(IEKF)

它比扩展卡尔曼多了个“迭代”，这个“迭代”是在同样也是按照"当前值处展开->估计->估计值处展开->再估计"的循环进行的，它和EKF的那个良性循环的区别在于，这是在一个kalman更新周期内进行的。这样做比单纯的EKF的好处在于，每次的精度损失会更小。

3) 粒子滤波(PF)

粒子滤波强行回避了非线性问题，既然非线性无论怎么近似都有误差，无法根据先验用表达式给出预测的分布的解析表达，那么就回归分布的本源，用统计来做。按照先验的分布随机给出一定数量的值，把这些值按照传递函数运算得到观测的预测，那么我们就可以得到同样数量的预测值，直接对这些值进行概率统计，不就可以得到它的分布了吗。这些值就是粒子，这种用粒子解决估计问题的方法就是粒子滤波。通过原理可以看出，粒子滤波属于贝叶斯估计，而不是最大后验估计，粒子滤波也是这些滤波算法中唯一的一个贝叶斯估计。当然粒子滤波也有它自己的问题，为了得到精确的分布，粒子的数量必须足够多，而且非线性越强，对数量的要求就越高，这意味着计算量的增加。除了计算量以外，更严重的是粒子退化问题，基本上大部分粒子滤波的研究都是为了解决这个问题。

4）无迹kalman(UKF)

UKF既不想做线性化，又不想采取像PF那样暴力的做法，而是采取了一种中庸的思想，只使用少量粒子来找出预测的分布，既然数量比较少，就不能浪费，于是在均值和均值两侧按照一定距离去设计点的位置。

5. 怎么选

有了多种方法，必然会面临怎么选的问题。面对实际问题，很少有绝对的线性，也很少有绝对的高斯，一切只是接近，是否要把它当做非高斯来处理，要看这种接近能达到什么程度。

1) 什么时候用KF

当有高精度惯导时，虽然它的完整模型时非线性的，而且是强非线性，但是由于惯导精度高，可以把状态量都当成小量，这时候就可以把矩阵中的一些三角函数简化，比如 ， ，除此之外，还可以把小量之间的相乘直接消掉，即 ，所以大家看到的高精度惯性导航的状态方程都是线性的，除了一些还未完成初始对准，即失准角比较大的情况。

2) 什么时候用EKF和IEKF

首先是状态误差无法用小量来近似，必须用非线性形式来表达的时候。其次则是在无人机里场出现的，直接用全量而不是误差量进行建模的情况，比如直接用姿态的四元数做状态量，而不再是失准角。同样的，能用EKF的地方都可以用IEKF。

3) 什么时候用PF

首先是状态模型的非线性非常强，但这种在多传感器融合定位中其实还比较少见，多数是能够用雅克比进行展开的。在实际工程中使用PF更多地是因为它的另一个优点，即它不要求噪声是高斯的。在低成本的多传感器融合中，这一点太重要了，如果你仔细看过低精度mems的实验数据，会发现它和高斯真的离得太远了，低成本的观测也是同样问题。由于影响滤波器精度和稳定性的除了模型，还要噪声，因此在这种情况下，优先采用PF有时候会是更合理的选择。

4) 什么时候用UKF

UKF其实用的比较少，这是它的特性决定的，当非线性不强的时候，EKF已经够用，当非线性和非高斯性强的时候，精度又不如PF，所以除非你正好有一定的非线性，但是对运算量的要求又很高，则可以用UKF。Cartographer的早期版本用的就是UKF，只不过现在的新版本已经用图优化来做融合了。

 

 

上一篇：组合导航系列文章（十一）：惯性导航误差传播规律

下一篇：组合导航系列文章（十三）：构建一个基本的组合导航系统

 

编辑于 07-06