ACS Energy Lett.：双原子位点氧电催化的表面曲率效应

研究背景

金属−氮碳（M−N−C）材料是一种很有前途的催化剂候选材料。它们的活性可以通过不同的电子和几何性质来调节，比如孔隙度。由于孔隙率建模的困难，具有可变表面曲率的M−N−C在很大程度上仍未被探索。塔尔图大学Nadezda Kongi和丹麦哥本哈根大学Vladislav Ivaništšev的等人建立了一个真实的孔内双原子位M−N−C模型，并应用密度泛函理论研究了表面曲率对氧还原和进化反应的影响，探究表面弯曲与催化能量势垒的关联。本研究希望通过预测调节表面曲率来提高单功能和双功能氧电催化的催化活性。

计算方法

本文的自旋极化密度泛函理论（DFT）计算采用GPAW 22.1和ASE 3.22.1软件在有限差分模式下使用修正的RPBE泛函进行。对于优化和能量计算，使用了3×1×1 k点采样，网格间距为0.18Å，至少5Å真空层，以及在0.1eV/Å以下的力最小化。原子区域用PAW形式处理，色散校正采用D4法进行解释。相关数据可通过网页查询：https://nano.ku.dk/english/research/theoretical-electrocatalysis/katladb/surface-curvature-effect-on-oxygen-electrocatalysis/.

结果与讨论

对于ORR和OER，主要的限制是两个关键中间体OH和OOH的比例关系。图1说明了M−N−C模型在DFT水平上解决OH−OOH缩放关系的演变。最简单的模型是由四个氮原子围绕嵌在石墨烯层中的金属原子(MeN4)组成的单原子位点催化剂(图1a)。改变MeN4位点上的金属中心同时成比例地改变所有中间体的吸附能；因此，它受到OH−OOH比例关系的限制MeN4模型的最新改进是Me2N6模型(图1b)，—由四个氮原子围绕两个金属原子形成的双原子位点催化剂。这些位点的组合变化可以更好地控制吸附能，此外第二个金属原子可以帮助解离O2，从而实现一种可能规避OH−OOH缩放关系的替代机制。然而，Svane等人发现，对于Co2N6，限制步骤是OH解吸，因此，打破比例关系并不会改善过电位。

Me2N6的替代品是一种模拟细胞色素c氧化酶的双原子催化剂其中一个模型是图1c所示的双卟啉体系，它是一种双原子位点催化剂，可以实现不包括OOH和缩放关系之间切换的替代反应机制。遗憾的是，这种人工模型需要不切实际的原子级控制来制造真正的电极。本工作提出了一个现实的孔内双原子位点M−N−C模型，展示了表面曲率如何影响ORR和OER的活性，超出了OH−OOH尺度关系的限制。作者提出了一个具有两个MeN4位点的弯曲模型（图1d），一个孔内双原子位点催化剂，我们在下面展示，它也可以在尺度关系之间切换，同时提供对所有吸附能更精确的控制。该模型可以研究真实M−N−C材料的主要内在特征的变化：原子距离和表面曲率。

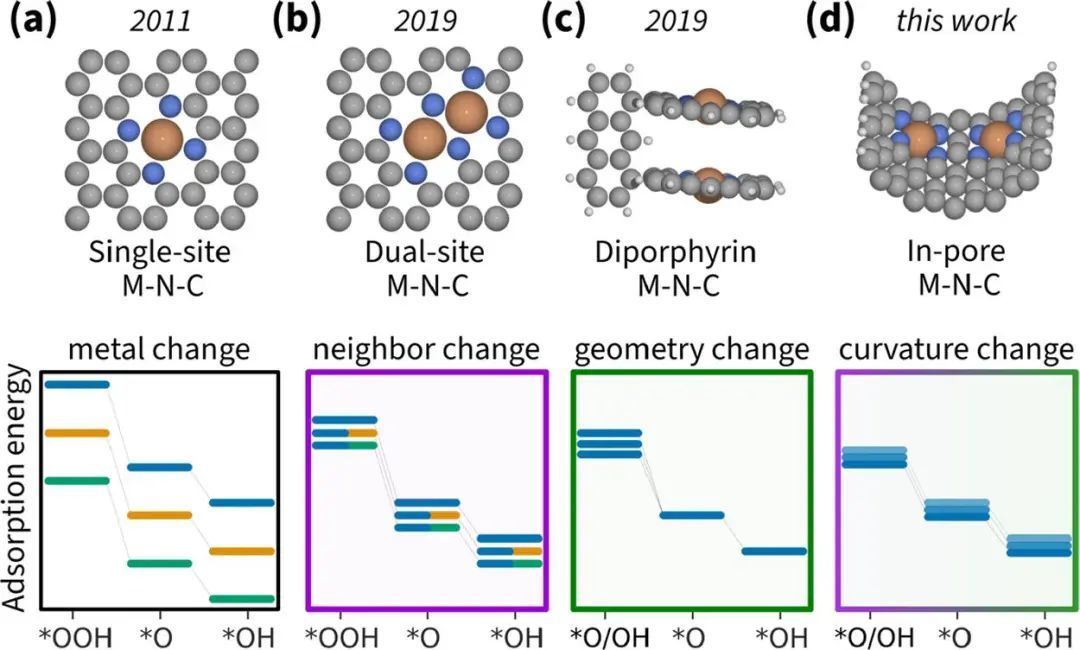
图1 M-−N-−C模型开发的时间轴。中间体的吸附能随其变化规律

表面曲率是所有多孔碳材料的共同参数。更具体地说，对于纳米管和圆柱孔，表面曲率是内半径(r)的倒数。弯曲模型(r = 4，6，8，8.5 Å)表示微孔内的表面曲率程度，而平面模型(r =∞)是通常吸附行为的参考点。为了构建模型，从扶手椅纳米带开始，引入两个MeN4位点，然后将表面弯曲到所需的半径，如图2所示。扶手椅纳米带的宽度选择，使得新插入的MeN4位点远离纳米带的边缘。因此，相互作用与所选择的纳米带类型无关，而扶手椅纳米带的选择是由于方便的对称性。我们考虑了两种模型:两个CoN4位点和CoN4 +一个NiN4位点。这些模型分别被称为CoCo和CoNi模型。钴的选择基于单位点催化剂的最佳吸附能的现有信息；选择镍作为次要的结合位点来比较次要位点的效果。

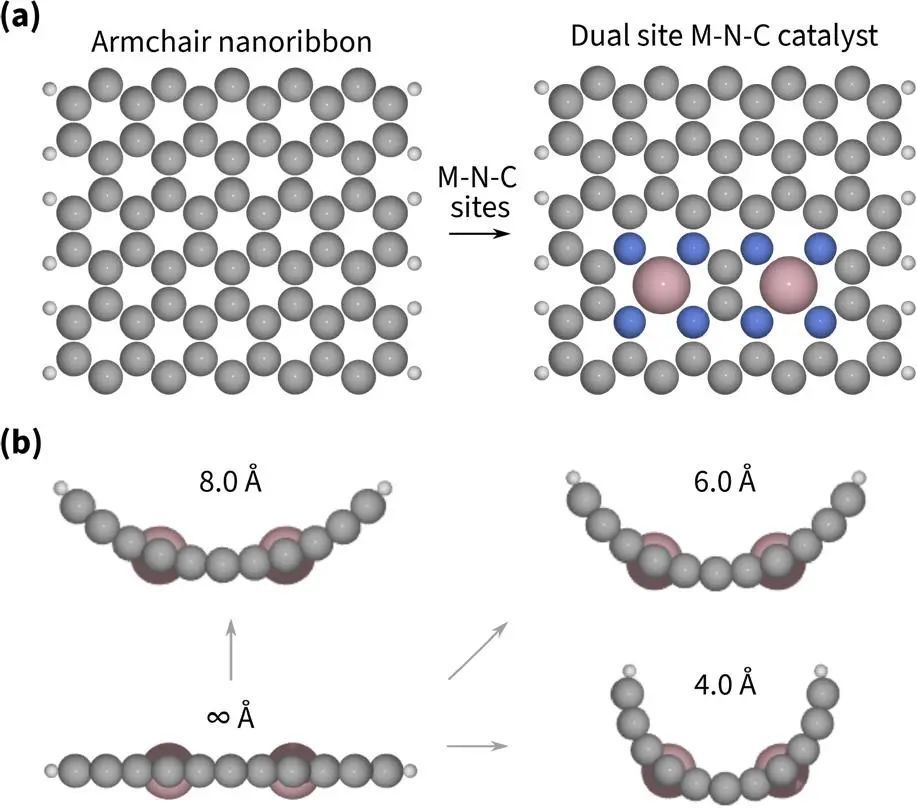
图2  从扶手椅纳米带构建双原子位点M−N−C模型的俯视图和侧视图

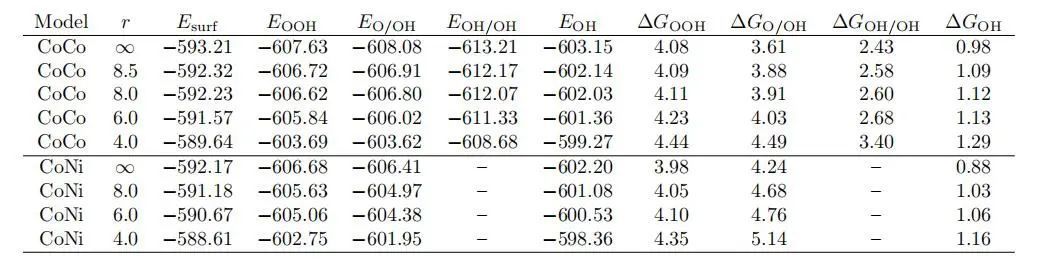
表面曲率在结合和解离机制中影响每个ORR中间体的吸附能（图3a，原始DFT能量数据见表1）。图3b，c中ΔGOOH和ΔGO/OH对孔隙半径的依赖关系有两个分量。图3b、c中的黑条表示CoCo和CoNi模型在等半径下的ΔGOOH吸附能相似。表面结合机制是由于OOH的弱邻近效应和与CoN4位点较好的强结合。相比之下，图3b，c中的彩色条和白色条表示CoCo模型的ΔGO/OH吸附能低于CoNi模型。这可能是由于OH与NiN4位点的结合较弱而导致的分离机制。再看曲率对吸附能的影响，图3a、b中的数据显示，吸附能随半径的增大有明显的下降趋势。这种下降与弯曲时电子结构的变化有关。由于两种中间体（O和OH）同时吸附，而不是一种中间体（OOH），因此解离机制的下降幅度比结合机制的下降幅度更大。最重要的是，将CoCo模型表面从平面弯曲到8Å，将吸附能调整到理想值3.69eV（绿色水平线）。然而，除了达到理想的吸附能外，更重要的是调整能量差以实现有效催化。

图3 ORR中间吸附能的结合和解离机制表1 DFT计算吸附中间体的能量（eV）

对于解离机理，表面弯曲可以调节两种中间体吸附能的差值。图4显示了ΔGO/OH−ΔGOH和ΔGOOH−ΔGOH对位间距离的依赖关系，位间距离与孔半径的平方成反比，对于缔合机制，自由能差几乎与孔半径无关，接近于预期的OH−OOH比例关系3.2 eV。相反，对于解离机制，存在明显的ΔG∼r-2线性依赖关系。此外，对于CoCo模型，缩放关系的切换允许低于3.2 eV，接近2.46 eV的理想差值。然而，这对于理想的催化剂来说还不够，因为除了OH O/OH外，解离反应过电位还取决于O和OH/OH中间体。

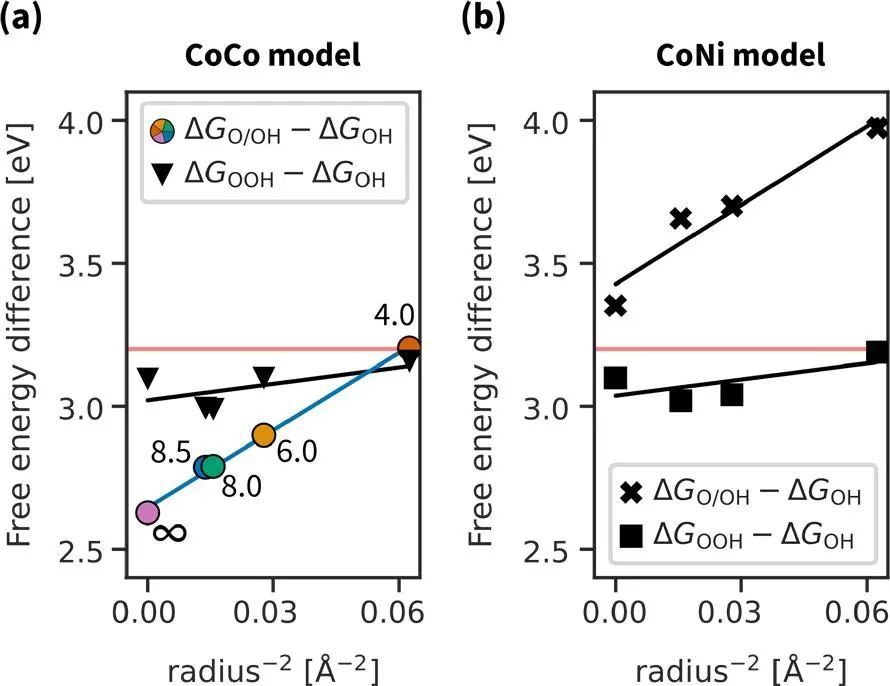
图4 自由能差与位点间距离的线性关系

在图5中，作者绘制了三维ORR过电位热图，并进一步将其推广到OER和双功能过电位。黑色的数据点（用于关联机制）位于比较线周围，比较线代表了文献中的MeN4能量，并服从OH−OOH尺度关系。彩色数据点（用于CoCo模型上的解离机制）遵循OH−O/OH尺度关系的虚线特征。随着孔隙半径的增加，这条线进入低过电位区域。ORR来说，虚线只有0.15 V远离火山顶部当孔隙半径略高于8 Å。OER关联在图5b，与ORR相比，过电位的下降幅度更大，而预测的半径−能量关系并没有显著改善OER活性。总体而言，双功能活性最高，模型的孔径分别为8.0和8.5 Å。

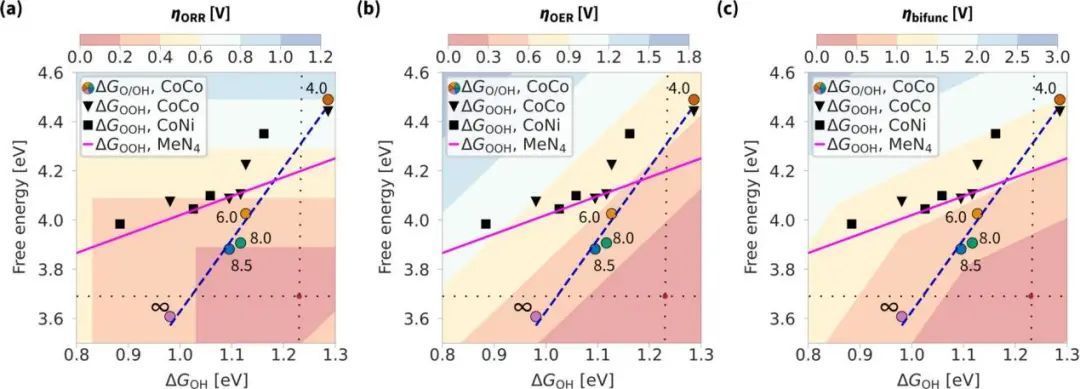
图5 (a) ORR、(b) OER和(c)双功能过电位的三维过电位热图

在图6中，计算在一个完整的自由能图来比较双功能氧催化的过电位变化。结果表明，将孔隙半径从8.0Å增加到8.5Å，ηORR减少，而ηOER增加。因此，在r = 8.5 Å左右达到了最佳的ηbifunc = 0.45 V。请注意，双功能过电位明显低于图5c中所示的过电位火山。更具体地说，无论直接计算的过电位为0.4 V，图5b中的ηOER电位约为0.25 V。一般来说，更精确的过电位计算（图6）预测的活性比近似ΔGOH≈2ΔGO时的给出的更高（图4）。

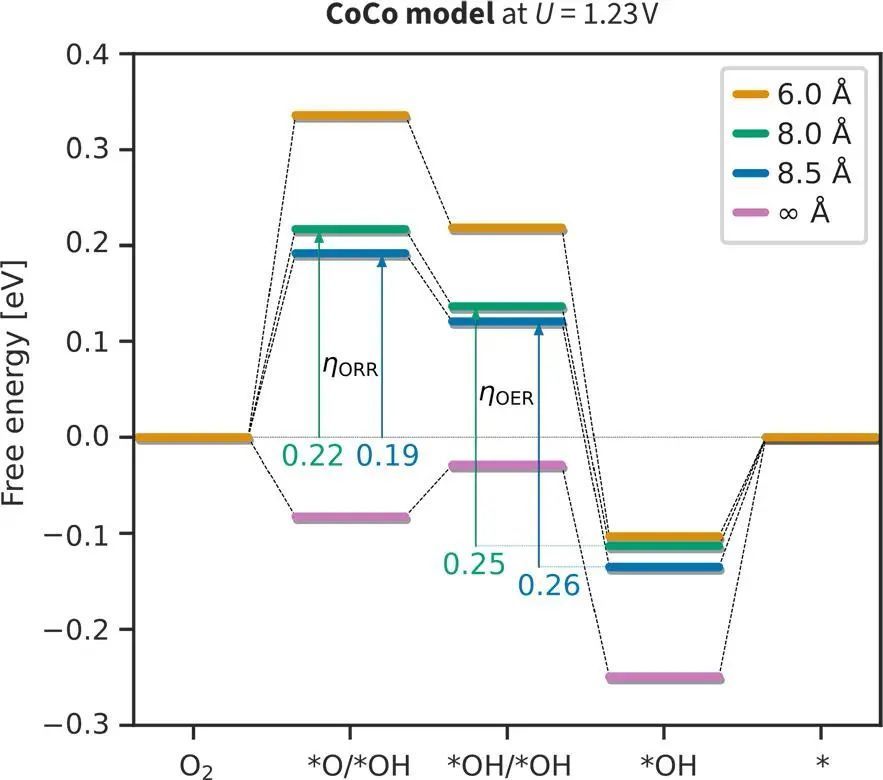
图6 ORR解离机制的自由能图

如上图所示，OOH与O/OH的解离将尺度关系从OH−OOH转变为更有利的OH−O/OH，理论上增加了活性。解离也排除了2e−还原为过氧化氢，这是已知的影响ORR对单原子位点催化剂的选择性。然而，活性和选择性都取决于反应动力学。表1和图S6中的数据表明，表面弯曲影响了反应动力学中的一个关键参数的解离势垒。在平面表面（r =∞）上，解离在热力学上是有利的，但高势垒使其在动力学上不可能。在一个强弯曲的表面（r = 4.0 Å）上，解离在热力学上是不利的（由于中间排斥），而势垒是有利的。随着金属距离的增加，解离屏障随着孔半径的增大而增大。因此，适度的曲度可以有效地平衡动力学、热力学（图3和4）、催化活性（图5和6）和选择性（图3a)。

结论与展望

综上所述，通过DFT计算，作者发现优化表面曲率可以将ORR过电位降低到0.20 V以下，并实现低至0.45 V的双函数过电位，即低于OH−OOH比例关系设定的0.74 V。这一发现有望在燃料电池、电解槽和空气电池中的(双功能)氧电催化方面取得进展。所提出的双原子位点模型具有可调的曲率，同时保持沿孔的周期性，适合未来对孔内电催化的深入研究，如不同的金属中心，通过亲氧旁观者配体稳定，以及微动力学建模。

文献信息

Cepitis, R., Kongi, N., Rossmeisl, J., & Ivaništšev, V. (2023). Surface Curvature Effect on Dual-Atom Site Oxygen Electrocatalysis. ACS Energy Letters, 8(3), 1330-1335.

ht-tps://doi.org/10.1021/acsenergylett.3c00068