黎曼曲面Riemann Surface

最新推荐文章于 2024-09-14 06:47:11 发布

wujianming_110117

最新推荐文章于 2024-09-14 06:47:11 发布

阅读量2k

点赞数

分类专栏：嵌入式系统算法成像技术

吴建明

本文链接：https://blog.csdn.net/wujianing_110117/article/details/107384833

版权

黎曼曲面Riemann Surface
在这里插入图片描述
A Riemann surface is a surface-like configuration that covers the complex plane with several, and in general infinitely many, “sheets.” These sheets can have very complicated structures and interconnections (Knopp 1996,
pp. 98-99). Riemann surfaces are one way of representing multiple-valued
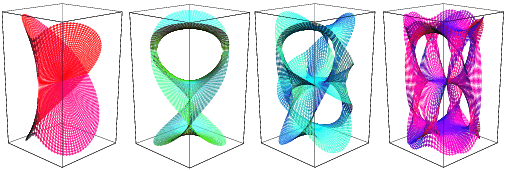
functions; another is branch cuts. The above plot shows Riemann surfaces for solutions of the equation

黎曼曲面是一种类似于曲面的结构，它覆盖了多个，通常是无限多个的“片”。这些片可以有非常复杂的结构和相互连接（Knopp 1996，pp.98-99）。Riemann曲面是表示多值函数（功能）的一种方法；另一种是分支切割。上图显示了方程解的黎曼曲面。
在这里插入图片描述
其中d=2, 3, 4, and 5, where w(z) is the Lambert W-function (M. Trott).