详解矩阵计算中的逆与伪逆，以及其在机器学习中的作用

GPT-4o

Poe

矩阵的逆和伪逆是线性代数中的重要概念，在机器学习中有着广泛的应用。以下从定义、计算方法及其在机器学习中的作用等方面详细解析矩阵的逆和伪逆。

---

一、矩阵的逆

1. 定义

矩阵 AAA 的逆矩阵（记作 A−1A^{-1}A−1）是一个矩阵，使得：

AA−1=A−1A=IA A^{-1} = A^{-1} A = IAA−1=A−1A=I

其中 III 是单位矩阵。

• 只有当 AAA 是 方阵（行数等于列数）且 满秩（行列式不为零）时，矩阵才是可逆的。

---

2. 计算

对于 n×nn \times nn×n 的可逆矩阵 AAA，其逆矩阵可以通过以下方法计算：

(1) 直接公式（仅适用于 2×22 \times 22×2 矩阵）

假设：

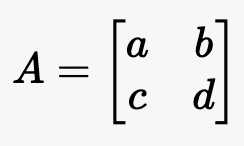
A=[abcd]

A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

A=[ac​bd​]

其逆矩阵为：

A−1=1ad−bc[d−b−ca]A^{-1} = \frac{1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}A−1=ad−bc1​[d−c​−ba​]

前提是 ad−bc≠0ad - bc \neq 0ad−bc=0（即满秩，行列式不为零）。

(2) 行列式与伴随矩阵法

对于 n×nn \times nn×n 的矩阵 AAA：

A−1=1det⁡(A)adj(A)A^{-1} = \frac{1}{\det(A)} \text{adj}(A)A−1=det(A)1​adj(A)

• det⁡(A)\det(A)det(A)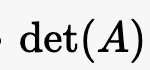：矩阵 AAA 的行列式。
• adj(A)\text{adj}(A)adj(A)：矩阵 AAA 的伴随矩阵。

(3) 高斯消元法

通过将 AAA 转化为单位矩阵 III，同时对单位矩阵 III 进行相同的行变换，最终得到 A−1A^{-1}A−1。

(4) 数值方法

对于大规模矩阵，通常使用数值方法（如 LU 分解）计算逆矩阵。

---

3. 在机器学习中的作用

(1) 求解线性方程组

给定线性方程组 Ax=bAx = bAx=b，如果 AAA 可逆，可以直接通过：

x=A−1bx = A^{-1} bx=A−1b

求解未知向量 xxx。

(2) 在线性回归中求解权重

在线性回归中，假设目标是最小化误差函数：

Loss=∥y−Xw∥2\text{Loss} = \| y - Xw \|^2Loss=∥y−Xw∥2

其闭式解为：

w=(XTX)−1XTyw = (X^T X)^{-1} X^T yw=(XTX)−1XTy

其中 (XTX)−1(X^T X)^{-1}(XTX)−1 是矩阵 XTXX^T XXTX 的逆。

(3) 特征变换和归一化

在特征变换中（如 PCA 的主成分变换），逆矩阵用于将数据从变换空间映射回原始空间。

---

二、矩阵的伪逆

1. 定义

伪逆（Moore-Penrose Pseudoinverse，记作 A+A^{+}A+）是对矩阵逆的一种推广，用于解决 非方阵 或 不可逆矩阵 的问题。

伪逆矩阵 A+A^{+}A+ 满足以下四个条件：

1. AA+A=AA A^{+} A = AAA+A=A
2. A+AA+=A+A^{+} A A^{+} = A^{+}A+AA+=A+
3. (AA+)T=AA+(A A^{+})^T = A A^{+}(AA+)T=AA+
4. (A+A)T=A+A(A^{+} A)^T = A^{+} A(A+A)T=A+A
5. 

伪逆存在且唯一，无论矩阵 AAA 是否为方阵、是否满秩。

---

2. 计算

(1) 基于奇异值分解（SVD）

伪逆最常用的方法是基于奇异值分解：

• 对矩阵 AAA 进行 SVD 分解：

• 

  A=UΣVT

• A = U \Sigma V^T

• A=UΣVT

  其中：

  • UUU：左奇异矩阵，维度为 m×mm \times mm×m。
  • Σ\SigmaΣ：对角矩阵，包含奇异值，维度为 m×n m \times nm×n。
  • VVV：右奇异矩阵，维度为 n×nn \times nn×n。

• 伪逆计算公式：

• 

  A+=VΣ+UT

• A^{+} = V \Sigma^{+} U^T

• A+=VΣ+UT

  其中 Σ+\Sigma^{+}Σ+ 是通过将 Σ\SigmaΣ 的非零奇异值取倒数后转置得到的伪逆矩阵。

(2) 特例：满秩方阵

如果 AAA 是满秩的方阵，那么伪逆与逆矩阵相同：

A+=A−1A^{+} = A^{-1}A+=A−1

(3) 数值方法

对于大规模矩阵，可以使用数值优化工具（如 NumPy 或 MATLAB）直接计算伪逆。

---

3. 在机器学习中的作用

(1) 解决线性方程组的最小二乘解

对于不可逆或非方阵的 AAA，直接求逆不可行。伪逆提供了一种解决方法：

x=A+bx = A^{+} bx=A+b

此解是最小化 ∥Ax−b∥2\| Ax - b \|^2∥Ax−b∥2 的最优解。

(2) 在线性回归中求解权重

如果 XTXX^T XXTX 不可逆（例如特征之间存在共线性问题），可以使用伪逆代替逆矩阵：

w=(XTX)+XTyw = (X^T X)^{+} X^T yw=(XTX)+XTy

(3) 奇异矩阵的处理

在神经网络等模型中，某些矩阵可能不可逆（如小批量训练中的协方差矩阵），伪逆可以代替逆矩阵，避免计算错误。

(4) 降维与正则化

伪逆在降维算法（如 PCA、LDA）中用于计算投影矩阵。同时，伪逆计算中的奇异值分解会忽略非常小的奇异值，因此具有一定的正则化效果（可避免过拟合）。

---

三、逆与伪逆的区别与联系

属性	逆矩阵	伪逆矩阵
适用矩阵	方阵，且必须满秩	任意矩阵（无论是否方阵或满秩）
计算方法	行列式、伴随矩阵、LU 分解等	奇异值分解（SVD）
存在条件	行列式不为零	一定存在
几何意义	完全精确的逆映射	最小二乘意义上的最佳近似逆映射
应用场景	方阵解线性方程组	非方阵或奇异矩阵解线性回归等问题

---

四、总结与应用场景

1. 逆矩阵：

   • 用于方阵的精确求解。
   • 应用场景：
     • 线性回归的闭式解（当 XTXX^T XXTX 可逆时）。
     • 特征变换（如 PCA 的逆变换）。

2. 伪逆矩阵：

   • 用于非方阵或奇异矩阵的近似求解。
   • 应用场景：
     • 线性回归（特征共线性或非满秩时）。
     • 奇异矩阵求解最小二乘问题。
     • 数据降维与正则化。

在机器学习中，伪逆比逆矩阵更常用，特别是在数据不完美（如矩阵不可逆或特征冗余）时，它提供了一种稳健的求解方法，是现代机器学习算法的重要工具。