ORBSLAM3中IMU初始化时重力方向的确定代码原理解析

诗筱涵

已于 2024-10-07 22:39:33 修改

阅读量796

点赞数 14

分类专栏：无人机-SLAM ORBSLAM 文章标签： ORBSLAM3

于 2024-10-07 22:36:00 首次发布

本文链接：https://blog.csdn.net/sinat_16643223/article/details/142747970

版权

无人机-SLAM 同时被 2 个专栏收录

199 篇文章 45 订阅

订阅专栏

ORBSLAM

3 篇文章 0 订阅

订阅专栏

首先确定重力方向初值的关键代码在ORB_SLAM3_detailed_comments/src/LocalMapping.cc
会由下面代码得到重力方向的初值之后再经过优化得到更为精确的重力方向的值，所以注意下面代码得到的是一个提供给优化的初值，不是要求一开始就得到一个非常准确的值，但是偏差也不能大了

    // Compute and KF velocities mRwg estimation
    // 在IMU连一次初始化都没有做的情况下
    if (!mpCurrentKeyFrame->GetMap()->isImuInitialized())
    {
        Eigen::Matrix3f Rwg;
        Eigen::Vector3f dirG;
        dirG.setZero();

        int have_imu_num = 0;
        for(vector<KeyFrame*>::iterator itKF = vpKF.begin(); itKF!=vpKF.end(); itKF++)
        {
            if (!(*itKF)->mpImuPreintegrated)
                continue;
            if (!(*itKF)->mPrevKF)
                continue;

            have_imu_num++;
            // 初始化时关于速度的预积分定义Ri.t()*(s*Vj - s*Vi - Rwg*g*tij)
            dirG -= (*itKF)->mPrevKF->GetImuRotation() * (*itKF)->mpImuPreintegrated->GetUpdatedDeltaVelocity();
            // 求取实际的速度，位移/时间
            Eigen::Vector3f _vel = ((*itKF)->GetImuPosition() - (*itKF)->mPrevKF->GetImuPosition())/(*itKF)->mpImuPreintegrated->dT;
            (*itKF)->SetVelocity(_vel);
            (*itKF)->mPrevKF->SetVelocity(_vel);
        }

        if (have_imu_num < 6)
        {
            cout << "imu初始化失败, 由于带有imu预积分信息的关键帧数量太少" << endl;
            bInitializing=false;
            mbBadImu = true;
            return;
        }

        // dirG = sV1 - sVn + n*Rwg*g*t
        // 归一化，约等于重力在世界坐标系下的方向
        dirG = dirG/dirG.norm();
        // 原本的重力方向
        Eigen::Vector3f gI(0.0f, 0.0f, -1.0f);
        // 求重力在世界坐标系下的方向与重力在重力坐标系下的方向的叉乘
        Eigen::Vector3f v = gI.cross(dirG);
        // 求叉乘模长
        const float nv = v.norm();
        // 求转角大小
        const float cosg = gI.dot(dirG);
        const float ang = acos(cosg);
        // v/nv 表示垂直于两个向量的轴  ang 表示转的角度，组成角轴
        Eigen::Vector3f vzg = v*ang/nv;
        // 获得重力坐标系到世界坐标系的旋转矩阵的初值
        Rwg = Sophus::SO3f::exp(vzg).matrix();
        mRwg = Rwg.cast<double>();
        mTinit = mpCurrentKeyFrame->mTimeStamp-mFirstTs;

其中最关键最核心的一部分代码是这句，这句也被程小六成为IMU初始化里面最难理解的一句，现在我们就这句进行分析。

            // 初始化时关于速度的预积分定义Ri.t()*(s*Vj - s*Vi - Rwg*g*tij)
            dirG -= (*itKF)->mPrevKF->GetImuRotation() * (*itKF)->mpImuPreintegrated->GetUpdatedDeltaVelocity();

其中计算式子所调用的两个函数的内容实现如下：

/** 
 * @brief 获得imu的旋转
 */
Eigen::Matrix<float,3,3> Frame::GetImuRotation() {
    return mRwc * mImuCalib.mTcb.rotationMatrix();
}

/** 
 * @brief 返回经过db(δba, δbg)更新后的dV,与上面是一个意思
 * @return dV
 */
Eigen::Vector3f Preintegrated::GetUpdatedDeltaVelocity()
{
    std::unique_lock<std::mutex> lock(mMutex);
    return dV + JVg * db.head(3) + JVa * db.tail(3);
}

所以下面这句代码实际对应dirG -= Rcb*IMU速度预积分测量值，即dirG =dirG - Rcb*IMU速度预积分测量值，这里看着是累减的形式，因为 $-g\Delta t_{ij}$ 前面是负号，实际产生的效果是累加， $-g\Delta t_{ij}$ 后面会具体说到。

            dirG -= (*itKF)->mPrevKF->GetImuRotation() * (*itKF)->mpImuPreintegrated->GetUpdatedDeltaVelocity();

在分析之前我们需要有IMU预积分的基础知识。

首先基于基本的牛顿力学可以推出下面

$R_{j}=R_{i}\prod_{k=i}^{j-1}Exp((\tilde{w}_{k}-b_{k}^{g}-\eta _{k}^{gd})\Delta t)$

$v_{j}^{w}=v_{i}^{w}+g^{w}\Delta t_{ij}+\sum_{k=i}^{j-1}R_{wk}(\tilde{a}_{k}-b_{k}^{a}-\eta_{k}^{ad} )\Delta t$

基于上面公式把基础坐标系由世界系变为相对于第i个imu帧，可以推出对应预积分公式，我们这里就用到速度层面的预积分
$\Delta R_{ij}\doteq R_{i}^{T}R_{j}=\prod_{k=i}^{j-1}Exp((\tilde{w}_{k}-b_{k}^{g}-\eta _{k}^{gd})\Delta t)$

$\Delta v_{ij}\doteq R_{iw}^{T}(v_{j}-v_{i}-g\Delta t_{ij})=\sum_{k=i}^{j-1}R_{ik}(\tilde{a}_{k}-b_{k}^{a}-\eta_{k}^{ad} )\Delta t$

上面是速度预积分的理论值，但是理论值是得不到的，实际可以算出的是测量值，理论值和测量值之间相差个噪声，速度预积分的测量值如下,其中 $\Delta v_{ij}$ 对应预积分理论值， $\Delta \tilde{v}_{ij}$ 对应不含噪声的且偏置未更新的预积分测量值，噪声因为没法测量，所以放在协方差里面，在联合优化时起作用，来解决噪声不可测的问题， $\Delta \bar{\tilde{v}}_{ij}$ 对应不含噪声且偏置更新的预积分测量值，也就是真正进行使用的的IMU预积分测量值，GetUpdatedDeltaVelocity函数也是对应的这个。
$\Delta v_{ij}\doteq \Delta \tilde{v}_{ij}-\delta v_{ij}$
$\Delta \tilde{v}_{ij}=\sum_{k=i}^{j-1}\Delta \tilde{R}_{ik}(\tilde{a}_{k}-b_{i}^{a})\Delta t$

$\Delta \bar{\tilde{v}}_{ij}\doteq \Delta \tilde{v}_{ij}+\frac{\partial \Delta \tilde{v}_{ij}}{\partial b^{g}}\delta b_{i}^{g}+\frac{\partial \Delta \tilde{v}_{ij}}{\partial b^{a}}\delta b_{i}^{a}$

初始化的时候，由于重力方向还没有确定，重力对齐的世界系和尺度所以没有确定，所以初始化时的速度的预积分公式和普通的预积分公式有些小区别。包含尺度s，以及Rwg，因为此时的世界系并不是重力对齐的世界系，而是以初始化第一个图像帧的相机系作为的世界系。
$sv_{j}^{w}=sv_{i}^{w}+R_{wg}g^{g}\Delta t_{ij}+\sum_{k=i}^{j-1}R_{wk}(\tilde{a}_{k}-b_{k}^{a}-\eta_{k}^{ad} )\Delta t$
对应推导出的速度预积分可以写为，当然这是速度预积分的理论值，某种程度上可以认为 $R_{i}^{T}(sv_{j}-sv_{i}-R_{wg}g\Delta t_{ij})$ 等价于速度预积分，把这个再带入到dirG -= Rcb*IMU速度预积分测量值里面，可以认为等价于 $-=R_{cb}R_{i}^{T}(sv_{j}-sv_{i}-R_{wg}g\Delta t_{ij})$ ，在累减的时候，中间的vi会抵消掉，但是Rwg*g*t会不断累加，所以最终就得到dirG = sV1 - sVn + n*Rwg*g*t，经过足够多的叠加后，sV1 - sVn的影响其实很小了已经，dirG里面基本就是n*Rwg*g*t,所以可以认为累减后的dirG可以代表重力方向，这是从公式推导的层面看的，下面会从更本质的层面进行分析方便理解。
$\Delta v_{ij}\doteq R_{i}^{T}(sv_{j}-sv_{i}-R_{wg}g\Delta t_{ij})=\sum_{k=i}^{j-1}R_{ik}(\tilde{a}_{k}-b_{k}^{a}-\eta_{k}^{ad} )\Delta t$

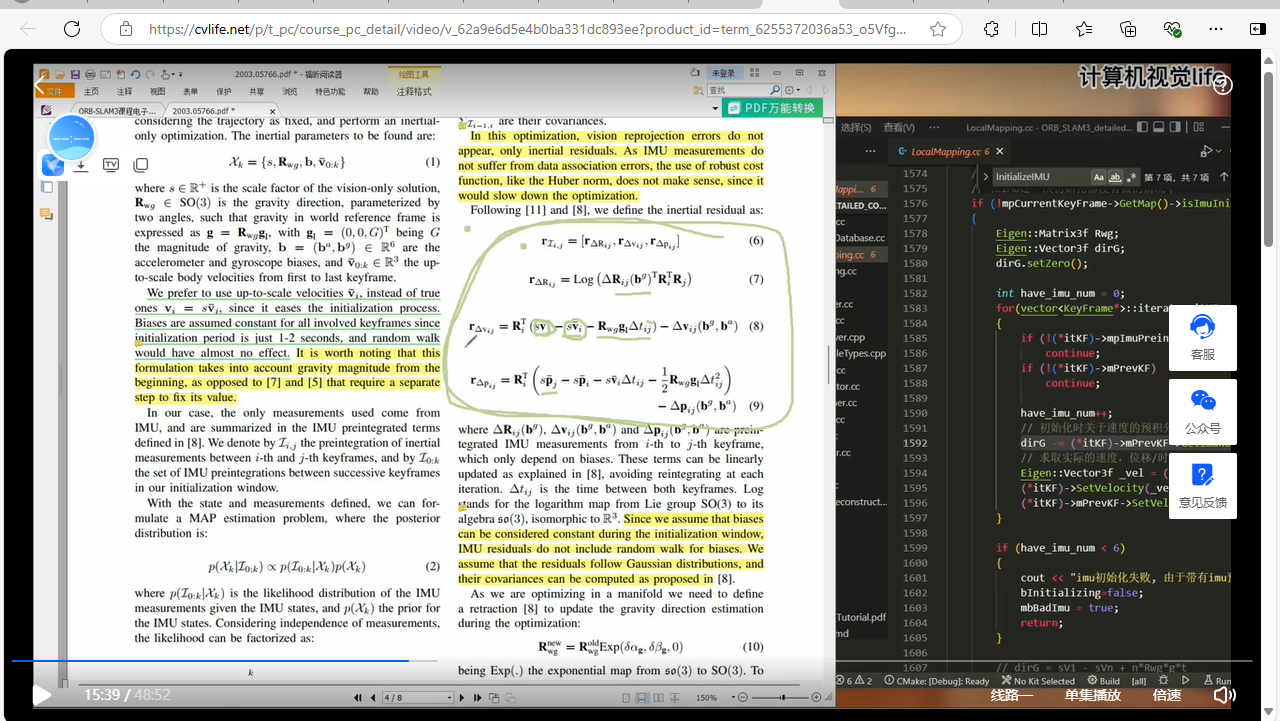
上面我们一方面可以从公式推导去理解,但是单纯的公式推导比较生硬，不容易理解本质，程小六ORBSLAM3课程里这块就是单纯从公式层面推导说的，这样很难真正看明白，只知道公式是这样，但是不清楚为什么是这样，所以我们也可以从基础的层面理解推导出
就是假如现在让我们自己去算出重力方向，最后可能也是选择这样基于旋转累加IMU数据得到是合适的方式，也就是把每帧IMU的加速度向量都转到第一帧imu坐标系下，然后叠加取平均。跟上面的思想方法其实本质一样，预积分知识多乘以一个 $\Delta t$ 再叠加罢了，这样也就很好理解了ORBSLAM3为什么是用这种方式去算出Rwg的初值。
预积分由于包含重力，所以可能不能单纯从某个物理量的层面去理解
下面这个速度预积分我们可以认为是基于第i帧imu系的，由于代码里是从第一个关键帧开始累加，可以认为是基于第一个imu帧坐标系了，再外乘以标定得到的相机IMU外参Tcb，那么可以认为是基于第一帧相机系的，而初始化的时候第一帧相机系就是作为世界系的，所以最终得到的可以认为是重力向量在图像世界系下的方向。
从代码里看，最终dirG = sV1 - sVn + n*Rwg*g*t，经过足够多的叠加后，sV1 - sVn的影响其实很小了已经。

$\sum_{k=i}^{j-1}R_{ik}(\tilde{a}_{k}-b_{k}^{a}-\eta_{k}^{ad} )\Delta t$

$R_{cb}\sum_{k=i}^{j-1}R_{ik}(\tilde{a}_{k}-b_k^a-\eta_k^{ad} )\Delta t=\sum_{k=i}^{j-1}R_{wk}(\tilde{a}_{k}-b_k^a-\eta_k^{ad} )\Delta t$

得到dirG也就是重力方向之后，我们还需要进一步算出Rwg。
因为最终是要把图像世界系的Z轴旋转到和重力方向一致，所以算重力方向和当前图像世界系Z轴间的夹角也没什么问题。

        // dirG = sV1 - sVn + n*Rwg*g*t
        // 归一化，约等于重力在世界坐标系下的方向
        dirG = dirG/dirG.norm();
        // 原本的重力方向
        Eigen::Vector3f gI(0.0f, 0.0f, -1.0f);
        // 求重力在世界坐标系下的方向与重力在重力坐标系下的方向的叉乘
        //计算向量 gI 和 dirG 的叉乘，结果向量 v 代表两个向量的垂直方向。叉乘可以用于找出旋转轴。
        Eigen::Vector3f v = gI.cross(dirG);
        // 求叉乘模长
        const float nv = v.norm();
        // 求转角大小
        //首先计算 gI 和 dirG 的点积，进而根据点积求出两者之间的夹角 ang。acos 函数用于将余弦值转换为角度。
        const float cosg = gI.dot(dirG);
        const float ang = acos(cosg);
        // v/nv 表示垂直于两个向量的轴  ang 表示转的角度，组成角轴
        //v 已经是一个垂直于 gI 和 dirG 的向量，通过乘以角度并与模长归一化后形成一个新的向量 vzg，它在旋转轴上
        Eigen::Vector3f vzg = v*ang/nv;
        // 获得重力坐标系到世界坐标系的旋转矩阵的初值
        //使用 Sophus 库中的 SO3f::exp 函数将轴角（vzg）转换为旋转矩阵 Rwg，表示从重力坐标系到世界坐标系的旋转。
        Rwg = Sophus::SO3f::exp(vzg).matrix();
        mRwg = Rwg.cast<double>();

它这相当于选择最短路径旋转，只要Z轴方向朝上就行，xy转成啥样就啥样
和三轴坐标系的旋转变换的区别是，它这只考虑了一个轴的旋转，而三轴坐标系的旋转需要考虑两个轴(第三个轴自动对上)，差别在这，我们可以另外多加个x轴的旋转对上，当然因为它这重力坐标系没有确定x轴，所以可能导致作者也没有去对x轴旋转对上imu_x_fusion里面是有确定重力系的x轴的。

就可以解释说明，D435i朝下时,跑单目IMU的ORBSLAM3，Rwg的初值可能有两种情况
重力对齐时是绕x轴转180度左右

重力对齐时是绕y轴转180度左右